LeetCode 69. x 的平方根

题目：
给定整数x，求\(\sqrt{x}\)

解法：
本题有两种常用解法，第一种自然是二分法，不再赘述，要注意的是可能会溢出，需要用long long。第二种是牛顿迭代法，利用导数逼近零点的方法。对于函数\(y=f(x)\)，我们任意取初始点\(x_0\)，然后不断迭代令\(x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)}\)，图示如下：

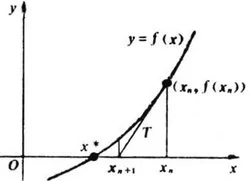
代码：

//二分法
class Solution {
public:
    int mySqrt(int a) {
        int l = 0, r = a, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long long)mid * mid <= a) {
                ans = mid;
                l = mid + 1;
            }
            else {
                r = mid - 1;
            }
        }
        return ans;
    }
};

//牛顿迭代法
class Solution {
public:
    int mySqrt(int a) { //要求a^0.5，即求y=x^2-a的零点，导数为y'=2x
        double x = 0, x_ = 1;
        while (floor(x_) != floor(x)) {
            x = x_;
            x_ = x - 0.5 * (x * x - a) / x;
        }
        return floor(x_);
    }
};