堆排序
算法思想
-
大根堆
堆其实是一种近似完全二叉树的数据结构,当树中所有的父节点的值都大于它的子节点的值时,这样的二叉树又
被称为大根堆; -
堆的存储方法
堆(二叉树)既可以使用数组表示,也可以使用链式节点表示,但是堆排序适用于对数组进行排序,无法对无序的
链式二叉树进行排序; -
数组表示二叉树时数组中元素的节点关系
- 数组下标从0开始
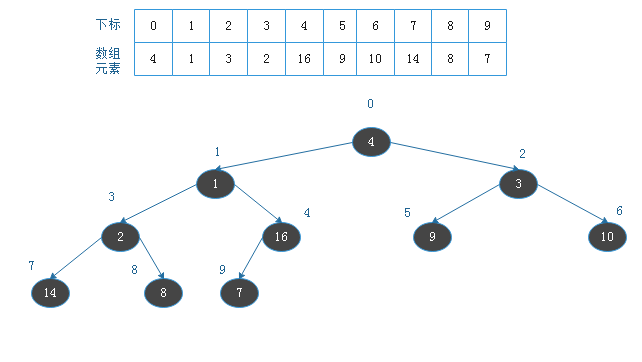
设有数组A[n],当数组下标从0开始时,从A[n/2]到A[n-1]均为叶节点;当下标i小于n/2时,数组元素A[i]的
左孩子为A[i+1],右孩子为A[i+2],但元素A[n/2-1]无右孩子
例:
![20190816105854.png]()
- 数组下标从1开始
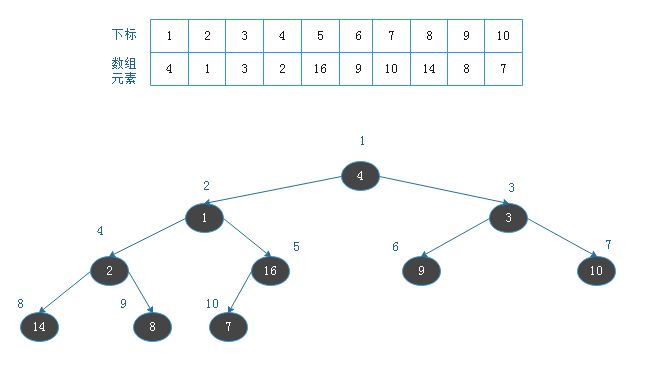
设有数组A[n],当数组下标从1开始时,从A[n/2+1]到A[n]均为叶节点;当下标i小于n/2+1时,数组元素A[i]
的左孩子为A[i],右孩子为A[i+1],但元素A[n/2]无右孩子
例:
![20190816110057.png]()
- 数组下标从0开始
-
保持大根堆性质
设数组A[n],对于任意下标元素Ai,其左右子树都是符合大根堆定义,但是A[i]有可能小于
左右孩子节点,此时要取左右孩子节点中最大的节点A[max]与A[i]进行交换,然后在对A[max]进行同样的操作
直到A[i]的子树符合大根堆的定义;
例:
![20190816130511.png]()
可以看出保持大根堆性质的调整是一个自"根"向"叶"的过程
代码实现:(数组下标从0开始)void KeepMaxHeapify(int * pAry, int nStartIndex, int nHeapSize) { int nIndexOfLeftChild = 2 * nStartIndex + 1; int nIndexOfRightChild = nIndexOfLeftChild + 1; int nIndexOfLagestChild = nStartIndex; if (nIndexOfLeftChild < nHeapSize && pAry[nIndexOfLeftChild] > pAry[nStartIndex]) { nIndexOfLagestChild = nIndexOfLeftChild; } if (nIndexOfRightChild < nHeapSize && pAry[nIndexOfRightChild] > pAry[nIndexOfLagestChild]) { nIndexOfLagestChild = nIndexOfRightChild; } if (nIndexOfLagestChild != nStartIndex) { int nTemp = pAry[nStartIndex]; pAry[nStartIndex] = pAry[nIndexOfLagestChild]; pAry[nIndexOfLagestChild] = nTemp; KeepMaxHeapify(pAry, nIndexOfLagestChild,nHeapSize); } }
时间复杂度分析:
这个算法的递归调用前代码的时间复杂度可以看作常量,其时间复杂度为T(n)=T(x)+Θ(1),其中x表示某个根节
点子树中的节点个数;堆是一个近似的完全二叉树,假设处于底层半满的最坏情况下,设树高为k,节点总数为n,
则n=2(k)-1+2(k-1)=3*2^(k-1)-1,完全二叉树根节点的左子树中节点总个数,与等高的满二叉树根节点的
左子树节点总个数相同,所以当前完全二叉树根节点左子树节点总个数为2^k-1,此时当前完全二叉树根节点的
左子树的节点总个数占整个完全二叉树节点个数的比例为(2k-1)/(3*2(k-1)-1)=2/3,所以在这种最差情况
下完全二叉树的左子树的节点个数为2n/3,假设这种最差的情况发生在完全二叉树(堆)中的任意节点的子树中,
这也就意味着表达式中的x=2n/3,所以时间复杂度T(n)=T(2n/3)+Θ(1),则T(n)=O(lgn);根据二叉树的性质可以知
高度为k的二叉树节点数最多为n=2^k-1个节点,可以推出高度k至少为lg(n+1),lg(n+1)和lg(n)相差无几,所
以可以认为k=lg(n),那么可以推出T(n)=O(lgn)=O(k); -
将无序数组建转换成大根堆
从数组中下标最大的非叶节点开始调整,直至根节点被调整后,大根堆建立完成,对于下标从0开始的数组,
从下标为n/2-1的节点开始调整,直至调整到下标为0的节点(根节点),对于下标从1开始的数组,从下标n/2开始
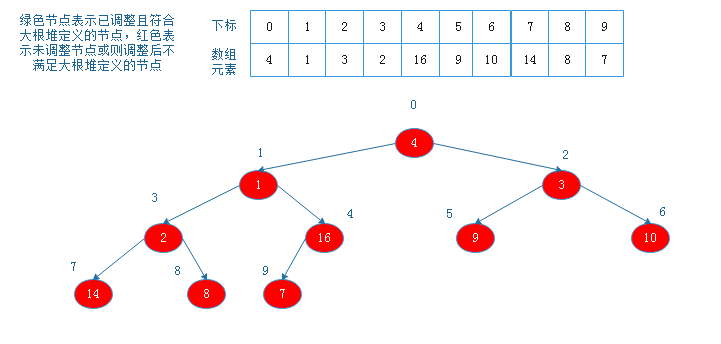
直至调整到下标为1的节点。例:
![20190816215259.png]()
元素共10个,下标最大的非叶节点的下标为4,调整完成后如下:
![20190816214103.png]()
接着对下标为3的根节点进行调整:
![20190816214337.png]()
对下标为2的节点进行调整:
![20190816214451.png]()
对下标为1的节点进行调整:
![20190816214729.png]()
调整后右子树不满足大根堆定义,则调整右子树:
![20190816214927.png]()
对下标为0的节点进行调整:
![20190816215125.png]()
调整后左子树不满足大根堆定义,则调整左子树:
![20190817152748.png]()
![20190817152711.png]()
代码实现:
void BuildMaxHeap(int * pUnSortAry, int nSize) { int nMaxIndexOfNonleaf = nSize / 2 - 1; for (int nIndex = nMaxIndexOfNonleaf; nIndex >= 0; nIndex--) { KeepMaxHeapify(pUnSortAry, nIndex, nSize); } }
时间复杂度分析:
对于一个有n个节点的堆,高度为k的节点,最多有n/2^(k+1)个,而堆的高度为lgn,所以BuildMaxHeap的时间
复杂度为为:
![20190817145717.png]()
可推得为O(n); -
堆排序
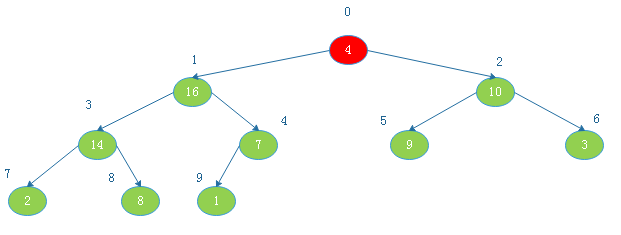
从大根堆的性质可以看出,根节点是当前数组中的最大值,为了进行升序排列,将根节点与数组中最后一个元素
进行交换,然后将这个最大节点从堆中剔除,在从新根节点开始进行调整,调整完成后在将新的根节点与数组中的倒数第二个节点交换,然后将这个最大节点从堆中剔除并调整再交换,......,直至堆中只剩根节点
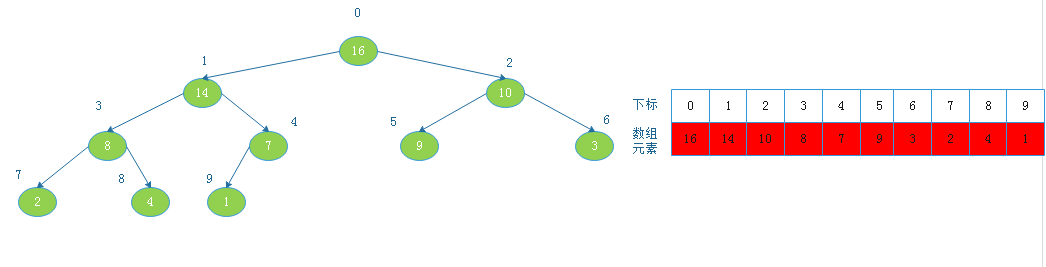
例:
![20190817153237.png]()
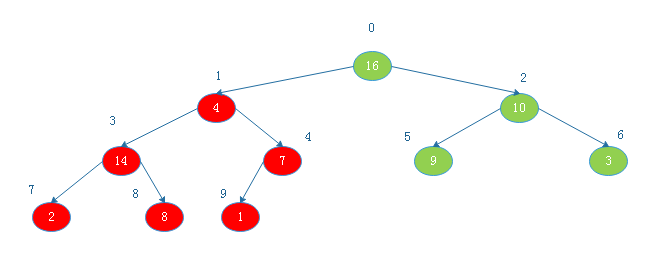
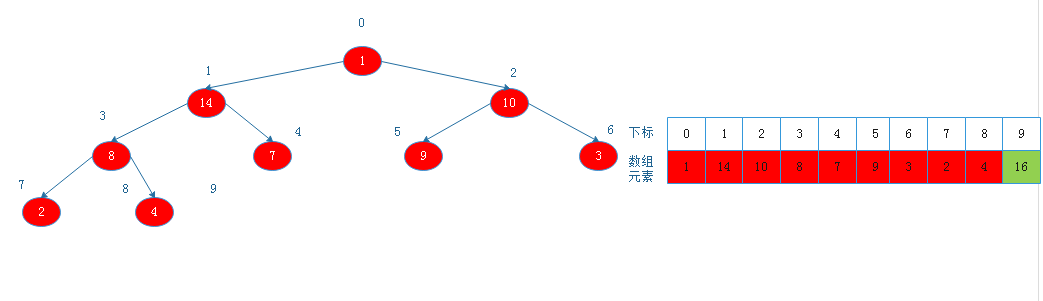
将根节点16与数组中下标为9的节点交换后:
![20190817153325.png]()
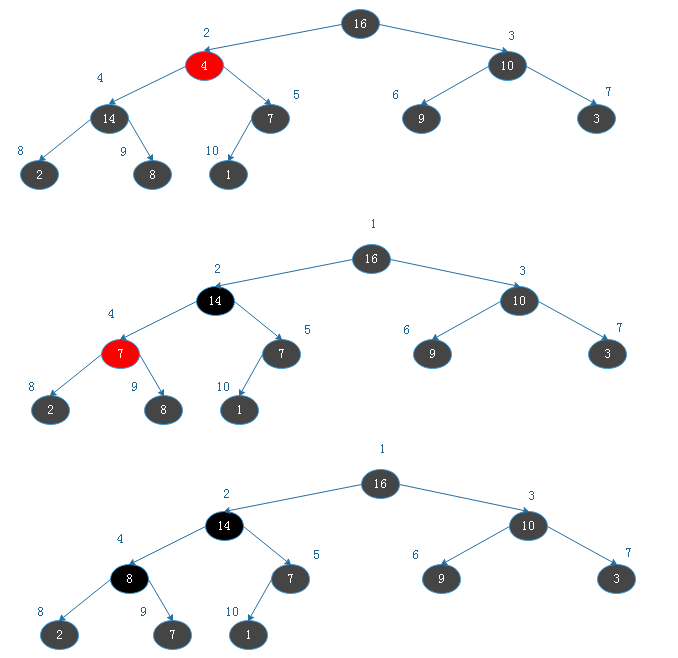
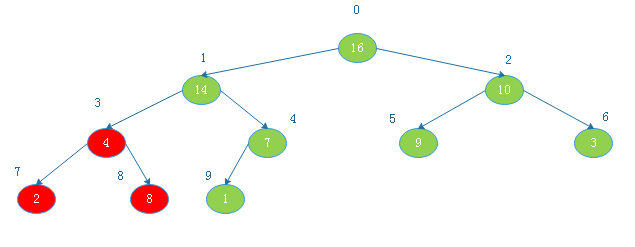
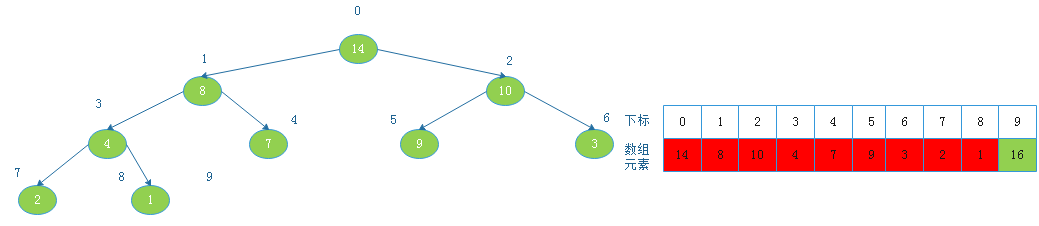
由上图看出,此时以1为根节点的二叉树不满足大根堆定义,则调整:
![20190817154038.png]()
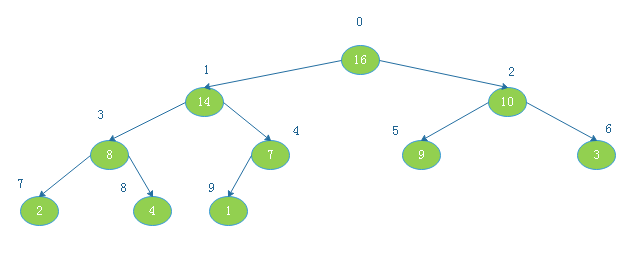
将根节点14与下标为8的节点交换后:
![20190817154236.png]()
由上图看出,此时以1为根节点的二叉树不满足大根堆定义,则调整:
![20190817155042.png]()
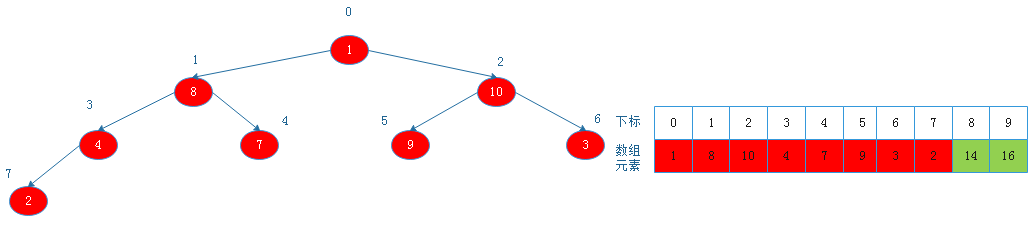
将根节点10与下标为7的节点交换后:
![20190817155213.png]()
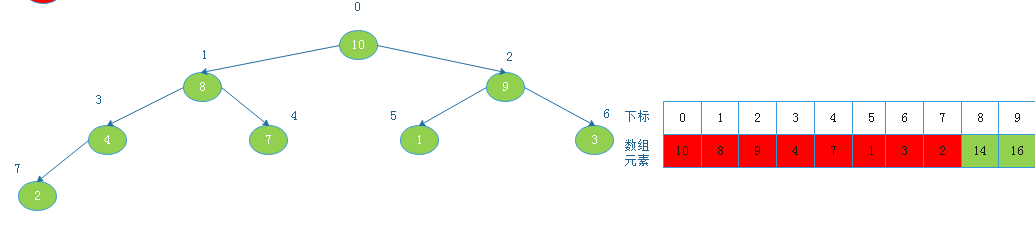
由上图看出,此时以2为根节点的二叉树不满足大根堆定义,则调整:
![20190817155454.png]()
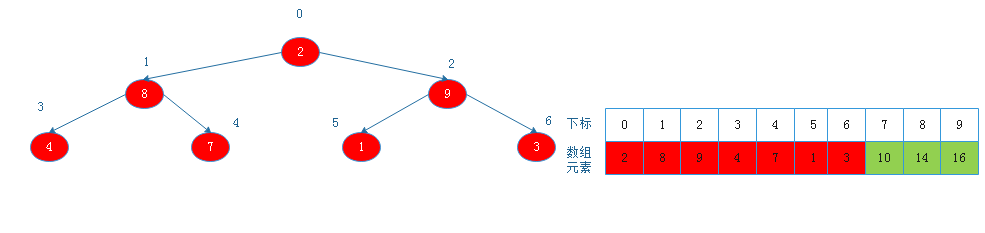
将根节点9与下标为6的节点交换后:
![20190817155654.png]()
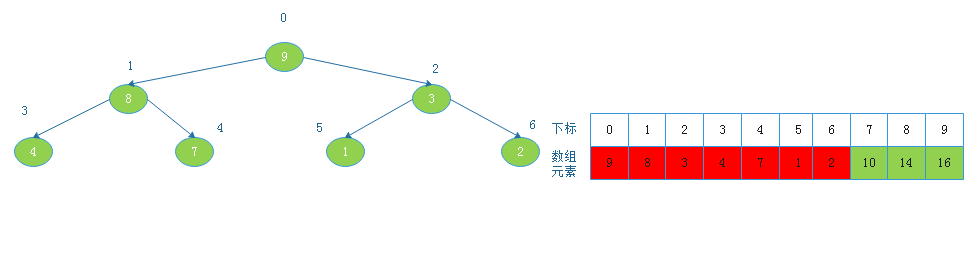
由上图看出,此时以2为根节点的二叉树不满足大根堆定义,则调整:
![20190817155817.png]()
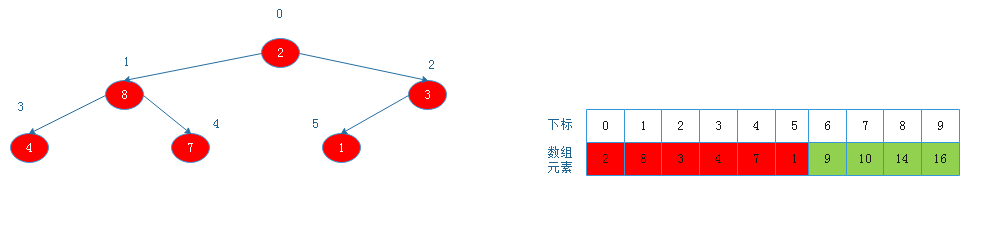
将根节点8与下标为5的节点交换后:
![20190817160017.png]()
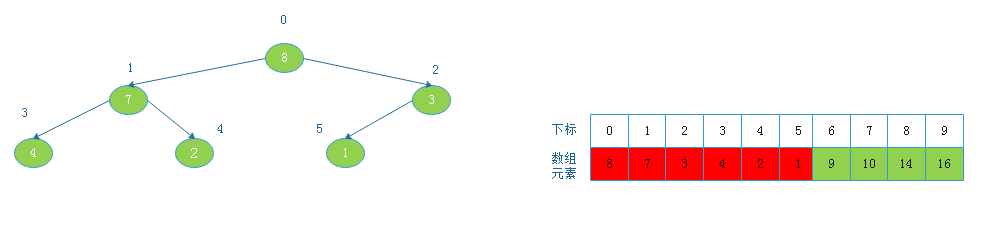
由上图看出,此时以1为根节点的二叉树不满足大根堆定义,则调整:
![20190817160155.png]()
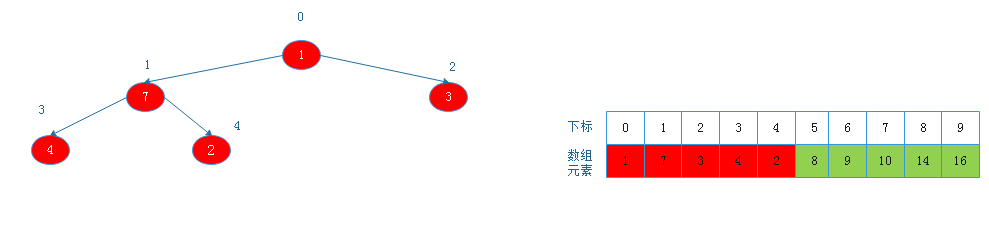
将根节点7与下标为4的节点交换后:
![20190817160420.png]()
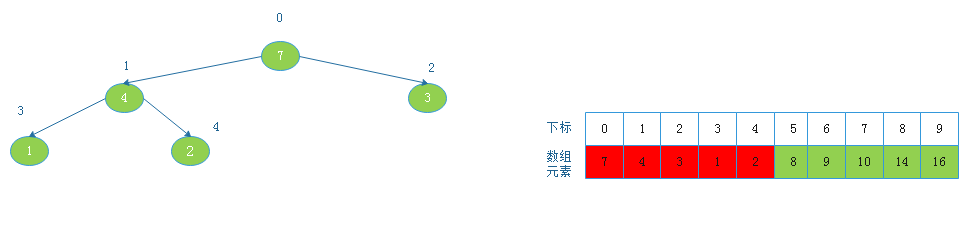
由上图看出,此时以2为根节点的二叉树不满足大根堆定义,则调整:
![20190817160539.png]()
将根节点4与下标为3的节点交换后:
![20190817160853.png]()
由上图看出,此时以1为根节点的二叉树不满足大根堆定义,则调整:
![20190817161040.png]()
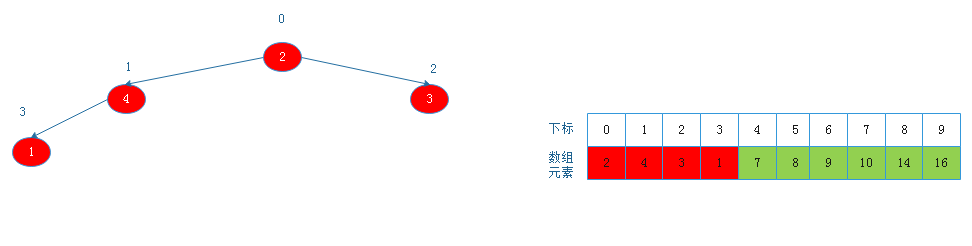
将根节点3与下标为2的节点交换后:
![20190817161328.png]()
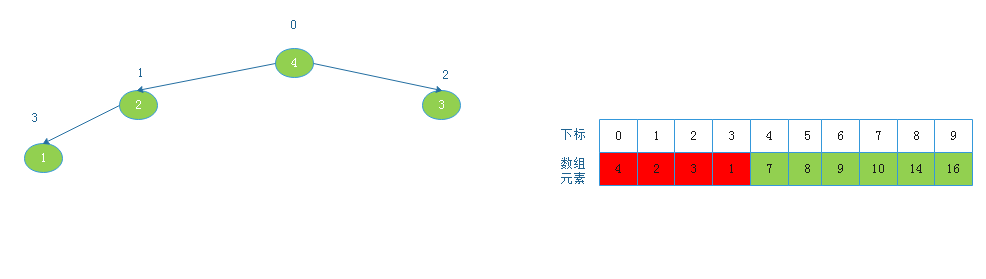
由上图看出,此时以1为根节点的二叉树不满足大根堆定义,则调整:
![20190817161407.png]()
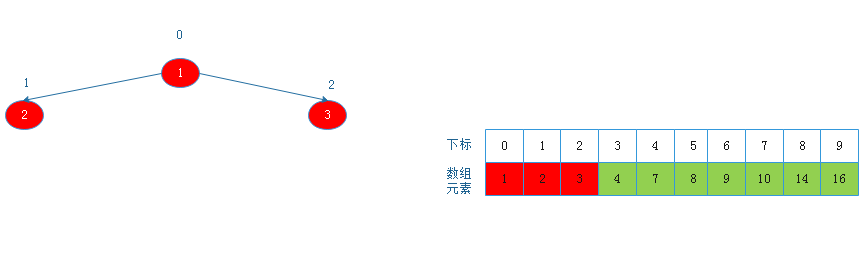
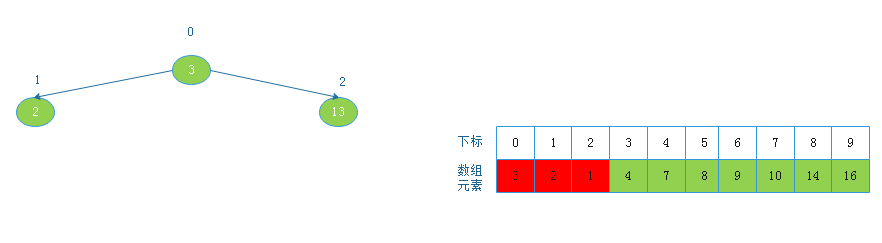
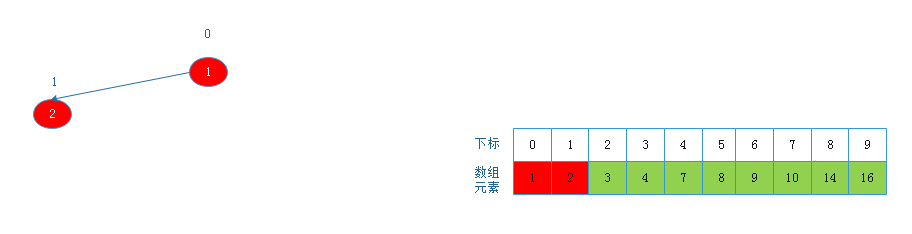
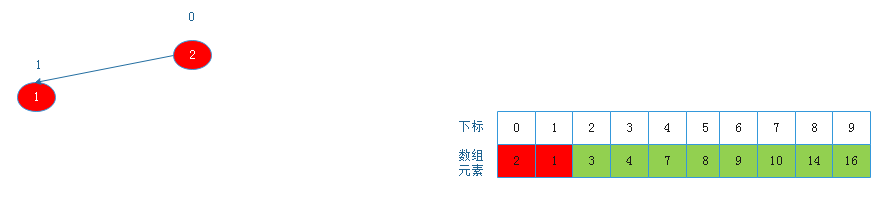
将根节点2与下标为1的节点交换后:
![20190817161622.png]()
此时堆中只剩一个节点,数组已经排序完成实现代码:
void HeapSort(int *pUnsortAry, int nSize) { BuildMaxHeap(pUnsortAry, nSize); for (int nLastIndex = nSize - 1; nLastIndex > 0; nLastIndex--) { int nTemp = pUnsortAry[nLastIndex]; pUnsortAry[nLastIndex] = pUnsortAry[0]; pUnsortAry[0] = nTemp; KeepMaxHeapify(pUnsortAry, 0, nLastIndex); } }
时间复杂度分析:
BuildMaxHeap时间复杂度为O(n),执行n-1次KeepMaxHeapify的时间复杂度为(n-1)lgn,所以总的时间复杂度
T(n)=O(n)+(n-1)lgn=nlgn;


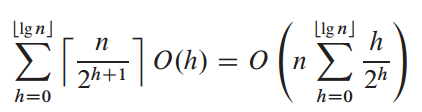


 浙公网安备 33010602011771号
浙公网安备 33010602011771号