进阶算法——树形DP

特点（特别之处）

DP这种东西…跟玄学一样…除非讲题，不然是真的没啥东西总结…

通过少量局部不完全不具代表性的刷题得出…

树形DP一般是在递归环境进行的，并且是先递到底

树形DP的第一维状态往往是以i为节点的子树。

题目中的ShowTime

因为动态规划的恐怖之处…所以还是多通过题目感受吧…

选课

 

 

 首先很容易看出来，这题的数据是二叉树。

对于某一个非根节点来说，如果你想选择这个节点，那么就必须选择他的父节点。

那么对于一个节点，如果左儿子选了y个节点，右儿子就一定是要选y-1-k个节点（因为父节点要选，需要扣除一个节点位）

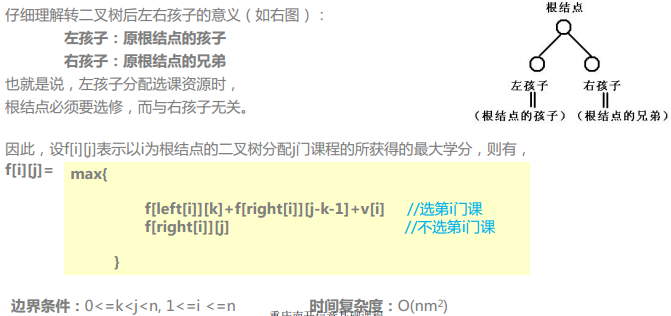
这样就可以推出状态，F[x][y]表示以x为根节点的子树，选择y个节点的最大值

那么就可以得到方程

F[x][y]=max(f[left[x][k]+f[right[x]]][y-1-k]+v[x])

枚举每个节点的左右儿子，循环k的值即可（0——y-1）

 选课2.0

 

 观察一下可以发现，这题又上道题数据是二叉树，变成了数据是森林。

我们如何处理森林的数据呢？首先将森林转换成一棵树。也就是说，对于全部的树，建立一个虚拟的根节点，让所有森林树的根连接虚拟根节点，让虚拟根节点成为“虚拟根”。这样，森林也就变成了一颗庞大的树。

如何让庞大的树变成二叉树？这里要引入一个口诀概念“左儿子右父亲”

也就是说，让这棵树的所有节点的左起第一个孩子变成他的左孩子，右起第一个兄弟变成右孩子。

 

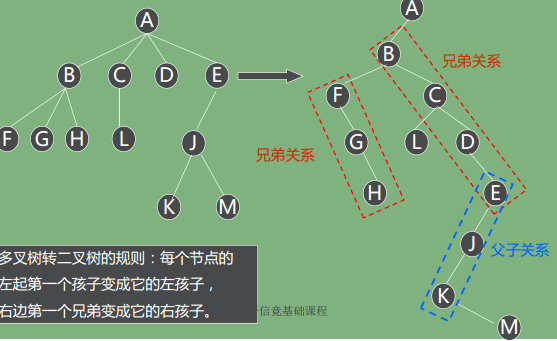
 那么如何实现这个操作呢？实际上只有两行代码

 

传送门 portal JZOJ 5906

 

 

 

 

Input
5
1 2 2
2 3 3
2 4 5
1 5 1
OutPut
13

惋惜的是，这道题当时在考试的时候错误的理解成了搜索之类的或者树生成。

看了题之后觉得有点昏，因为对于在哪里开门、开哪个门、如何判重等等十分疑惑。

但没想到是个树形Dp。

认真思考之后，确实是有如下规律：

1.我们不可能在某一子树尚未遍历完的情况下用传送门跑到别的子树

2.对于每个点的状态，无非只有开启传送门或不开启传送门

3.每条边都至少会被走一次，在没有门的情况下会走两次。至多情况下只走两次。

那么就可以设计一个方程式。以F[x]表示以x为根节点的子树遍历完返回所需要的最小时间。

那么 ，对于x的两种决策：

1：开启传送门，其子树中最长的那条只算一次（因为返回用门，无需二次遍历），其他的都算两次。也就是，设定y为子节点，len为最长条的长度，wealth表示根x到节点y的距离。该状态产生的结果为  Sum[y]*2-len[y]+wealth

2：不开启传送门，那么其所有子树下的所有边都将被遍历2次，也就是，设定y为x的子节点，以y为根节点的子树遍历完回到y的时间，加上x到y所需要的代价*2（往一次 ，返一次），便得到状态F[y]+wealth*2

对两种决策取较小者，要注意F[x]在遍历中是累加的，因为要遍历每一个x下的子节点y才能产生答案。

下面是代码。

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int MAXN=1000010;
struct Edge{
    int Wealth;
    int End;
    int Next;
}Edges[2000020];
int Head[2000020];
int idx;
void Add(int start,int end,int value){
    Edges[++idx].End=end;
    Edges[idx].Wealth=value;
    Edges[idx].Next=Head[start];
    Head[start]=idx;
}
long long F[MAXN];
long long Length[MAXN];
long long Sum[MAXN]; 
int a,b,c;
int n;
void Dfs(int x,int fa){
    for(int i=Head[x];i;i=Edges[i].Next){
        if(Edges[i].End!=fa){
            Dfs(Edges[i].End,x);
            Length[x]=max(Length[x],Length[Edges[i].End]+Edges[i].Wealth);
            Sum[x]+=Sum[Edges[i].End]+Edges[i].Wealth;
            F[x]+=min(F[Edges[i].End]+Edges[i].Wealth*2,Sum[Edges[i].End]*2-Length[Edges[i].End]+Edges[i].Wealth);
            
        }
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<n;i++){
        scanf("%d%d%d",&a,&b,&c);
        Add(a,b,c);
        Add(b,a,c);
    }
    Dfs(1,0);
    printf("%lld",F[1]);
}