排序算法之——归并排序(两种方法及其优化)
本文将围绕代码从多个方面分析归并算法,归并的操作很简单,稍加思考便能深刻理解。
1、算法思想:
要将一个数组排序,可以(递归地)将数组分成两半分别排序,然后将两边归并起来。归并算法最吸引人的地方是它能保证将任意长度为N的数组排序的时间与NlgN成正比。
主要缺点是需要与N成正比的额外空间。

(示意图1)
2、原地归并的抽象方法
实现归并最直截了当的方法是将两个数组归并到第三个数组,实现的方法很简单,从左到右逐一比较两数组的第一位元素,将小的一个放入第三个数组(假设两数组已经有序),完成操作后第三个数组就是有序的。了解了思路,我们直接看代码。
1 public static void merge(Comparable[] a, int lo, int mid, int hi) {
2 int i = lo, j = mid + 1;
3 for (int k = lo; k <= hi; k++) {
4 aux[k] = a[k];
5 }
6 for (int k = lo; k <= hi; k++) {
7 if (i > mid) {
8 a[k] = aux[j++];
9 } else if (j > hi) {
10 a[k] = aux[i++];
11 } else if (less(aux[i], aux[j])) {
12 a[k] = aux[i++];
13 } else {
14 a[k] = aux[j++];
15 }
16 }
17
18 }
主要操作就是第二个for循环里的四个判断:
1、数组1走完(将数组2当前元素放入数组3)
2、数组2走完(将数组1当前元素放入数组3)
3、数组1当前元素小于数组2当前元素(将数组1当前元素放入数组3)
4、数组2当前元素小于等于数组1当前元素(将数组2当前元素放入数组3)

(示意图2:将数组1和组2归并到组3)
3、自顶向下的归并排序
如果能将两个子数组排序,就能通过并归两个子数组来对整个数组排序,这一切是通过递归实现的,也叫递归归并。直接看代码:
1 public class Merge{
2 private static Comparable[] aux;
3 public static void sort(Comparable[] a) {
4 aux = a.clone();// 一次性分配空间
5 sort(a,0, a.length - 1);
6 }
7
8 private static void sort(Comparable[] a,int lo, int hi) {
9 if (hi <= lo) {
10 return;
11 }
12 int mid = lo + (hi - lo) / 2;
13 sort(aux,a, lo, mid);//左半边排序
14 sort(aux,a, mid + 1, hi);//右半边排序
15 merge(a,aux,lo, mid, hi);//归并结果(参考原地归并的抽象方法)
16 }
17 }
示意图:

(示意图3)
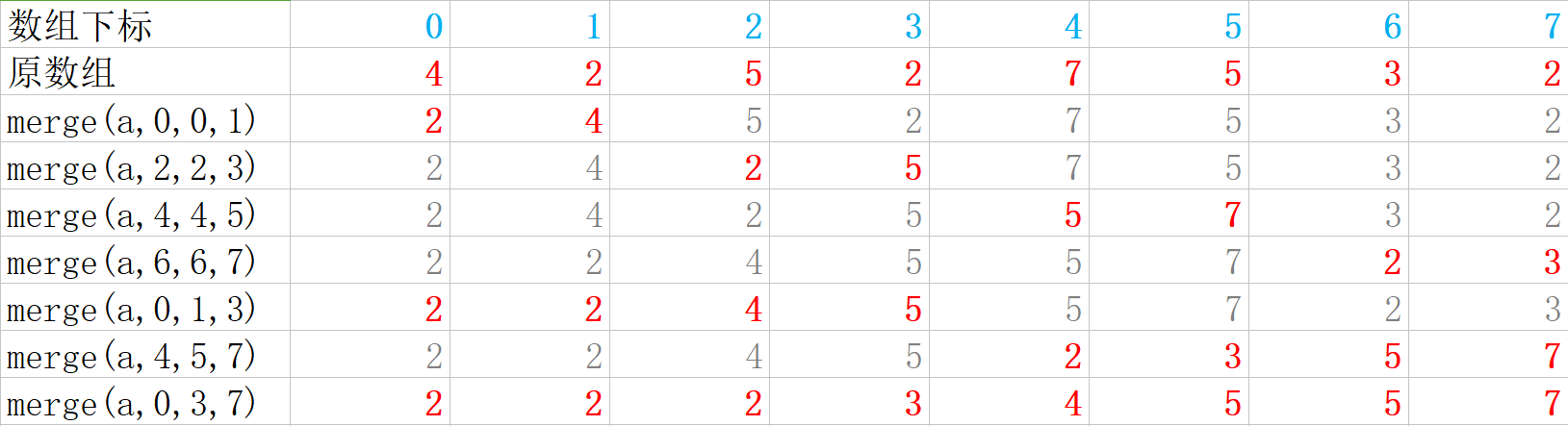
上图只是merge方法的轨迹,sort方法也极为重要,要想理解就必须知道sort方法调用的轨迹(这里请读者自己先写出sort的轨迹再看下面的答案)
sort(a,0,7)
将左半部分排序
sort(a,0,3)
sort(a,0,1)
merge(a,0,0,1)
sort(a,2,3)
merge(a,2,2,3)
将右半部分排序
sort(a,4,7)
sort(a,4,5)
merge(a,4,4,5)
sort(a,6,7)
merge(a,6,6,7)
归并结果
merge(a,0,3,7)
4、自底向上的归并排序
我们已经知道,自顶向下采用的是递归的方法,而自底向上则是循序渐进得解决问题,采用了循环的方法。通过下图可以很容易看出两种方式的区别:
下面上代码:
1 public static void sort(Comparable[] a) {
2 int n = a.length;
3 aux = new Comparable[n];
4 for (int sz = 1; sz < n; sz = sz + sz) {
5 for (int lo = 0; lo < n - sz; lo += sz + sz) {
6 merge(a, lo, lo + sz - 1, Math.min(lo + 2 * sz - 1, n - 1));// 最后一次并归的第二个子数组可能比第一个小此时lo+2*sz-1越界
7 }
8 }
9 }
读者自行考虑自底向上方法的运行轨迹。
5、三项优化(代码在后面的代码演示中)
①对小规模子数组使用插入排序
用不同的方法处理小规模数组能改进大多递归算法的性能,在小数组上上,插入排序可能比并归排序更快。
②测试数组是否有序
根据归并排序的特点,每次归并的两个小数组都是有序的,当a[mid]<=a[mid+1]时我们可以跳过merge方法,这样并不影响排序的递归调用。
③不将元素复制到辅助数组
我们可以节省将数组复制到辅助数组的时间,这需要一些技巧。先克隆原数组到辅助数组,然后在之后的递归交换输入数组和辅助数组的角色(通过看代码更容易理解)

(画方框的为每次的输出数组)
6、代码演示(java):
1 public class Merge implements Comparable<Merge> {// 归并排序(优化前)
2 private static Comparable[] aux;
3
4 private static boolean less(Comparable v, Comparable w) {
5 return v.compareTo(w) < 0;
6 }
7
8 @Override
9 public int compareTo(Merge arg0) {
10 // TODO Auto-generated method stub
11 return 0;
12 }
13
14 public static void merge(Comparable[] a, int lo, int mid, int hi) {// 原地归并的抽象方法
15 int i = lo, j = mid + 1;
16 for (int k = lo; k <= hi; k++) {
17 aux[k] = a[k];
18 }
19 for (int k = lo; k <= hi; k++) {
20 if (i > mid) {
21 a[k] = aux[j++];
22 } else if (j > hi) {
23 a[k] = aux[i++];
24 } else if (less(aux[j], aux[i])) {
25 a[k] = aux[j++];
26 } else {
27 a[k] = aux[i++];
28 }
29 }
30 }
31
32 public static void sort(Comparable[] a) {
33 aux = new Comparable[a.length];
34 sort(a, 0, a.length - 1);
35 }
36
37 private static void sort(Comparable[] a, int lo, int hi) {
38 /*
39 * 自顶向下的并归排序 三个改进
40 */
41 if (hi <= lo) {
42 return;
43 }
44 int mid = lo + (hi - lo) / 2;
45 sort(a, lo, mid);
46 sort(a, mid + 1, hi);
47 merge(a, lo, mid, hi);
48 }
49
50 private static void exch(Comparable[] a, int j, int i) {
51 // TODO Auto-generated method stub
52 Comparable temp;
53 temp = a[j];
54 a[j] = a[i];
55 a[i] = temp;
56 }
57
58 public static void main(String[] args) {
59 Merge mg = new Merge();
60 Comparable a[] = { 8, 1, 6, 8, 4, 6, 9, 7, 1, 2, 3, 4, 8, 5, 2, 6, 4, 3, 8 };
61 mg.sort(a);
62 for (int i = 0; i < a.length; i++) {
63 System.out.print(a[i] + " ");
64 }
65 }
66 }
1 public class MergeX implements Comparable<Merge> {// 归并排序(优化后)
2 private static Comparable[] aux;
3
4 private static boolean less(Comparable v, Comparable w) {
5 return v.compareTo(w) < 0;
6 }
7
8 @Override
9 public int compareTo(Merge arg0) {
10 // TODO Auto-generated method stub
11 return 0;
12 }
13
14 public static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {// 原地归并的抽象方法
15 int i = lo, j = mid + 1;
16 // for (int k = lo; k <= hi; k++) {
17 // aux[k] = a[k];
18 // }
19 for (int k = lo; k <= hi; k++) {
20 if (i > mid) {
21 a[k] = aux[j++];
22 } else if (j > hi) {
23 a[k] = aux[i++];
24 } else if (less(aux[j], aux[i])) {
25 a[k] = aux[j++];
26 } else {
27 a[k] = aux[i++];
28 }
29 }
30 }
31
32 public static void sort(Comparable[] a) {
33 aux = a.clone();// 一次性分配空间
34 sort(a, aux, 0, a.length - 1);
35 }
36
37 private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
38 /*
39 * 自顶向下的并归排序 三个改进
40 */
41 // if (hi <= lo) {
42 // return;
43 // }
44 int mid = lo + (hi - lo) / 2;
45 if (hi - lo <= 7) {// 对小规模子数组使用插入排序
46 //System.out.println("insert!");
47 insertionSort(a, lo, hi);
48 return;
49 }
50 sort(aux, a, lo, mid);
51 sort(aux, a, mid + 1, hi);
52 if (!less(aux[mid + 1], aux[mid])) {// 已经有序时跳过merge(a中lo到mid mid到hi分别都是有序的)
53 System.arraycopy(aux, lo, a, lo, hi-lo+1);
54 return;
55 }
56 merge(a, aux, lo, mid, hi);
57 }
58
59 private static void insertionSort(Comparable[] a, int lo, int hi) {
60 for (int i = lo; i <= hi; i++)
61 for (int j = i; j > lo && less(a[j], a[j - 1]); j--)
62 exch(a, j, j - 1);
63 }
64
65 private static void exch(Comparable[] a, int j, int i) {
66 // TODO Auto-generated method stub
67 Comparable temp;
68 temp = a[j];
69 a[j] = a[i];
70 a[i] = temp;
71 }
72
73 public static void main(String[] args) {
74 MergeX mgx = new MergeX();
75 Comparable a[] = { 8, 1, 6, 8, 4, 6, 9,7,1, 2, 3,4,8,5,2,6,4,3,8};
76 mgx.sort(a);
77 for (int i = 0; i < a.length; i++) {
78 System.out.print(a[i] + " ");
79 }
80 }
81 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号