排序算法之——快速排序

对于快速排序，相信大家都有听过，这是一个被封为圣经的算法，足以体现算法的神奇的伟大。接下来将从算法思想、算法具体实现、不同情况下的复杂度、算法的优化和代码展示等几个方面为读者深入讲解。

 

一、算法思想

快速排序是一种分治的排序算法，主要操作是进行一趟操作将数据分成两部分，左边的部分都比基准值小，右边的部分都比基准值大（非降序排序），切分的位置取决于数组的内容，再分别对两部分进行同样的递归操作。

了解二分查找的朋友应该很容易理解，不同的是，二分查找每次划分数据后只需对一边进行操作，所以它的速度更快（二分查找的复杂度为log2n,（以2为底，n的对数））。

快速排序是对冒泡排序的改进（冒泡排序是对相邻的两个元素比较。快速排序是找到一个基准点，将数据划分成两部分，对两部分进行递归操作）

快速排序之所以快，是因为它采用了分治法的思想，把一个大的数据，分成多个小的块，对小的块进行处理，再将处理后的小块合并再处理。

 

二、算法具体实现（三种实现）

1、前后指针法(重点介绍)

把前后指针法放到最前面，是因为它有独有的优势，由于指针只是单侧的移动，对于单链表等只支持单向移动的数据结构，它依然能派上用场（另外两种算法都需要两指针分别向后向前移动）。

①将数组最左的元素记为key，创建指针i和j，i指向数组最左边的元素，j指向i的下一位。

②比较array[j]和key：如果array[j]>key,j后移一位，i不动。若array[j]<key，交换i+1和j的值，ij同时后移一位。

③当j走到数组的末尾时，先执行②操作，再交换array[i]和key。

④对两边进行上述操作的递归操作。

一趟走完key左边的数都小于key，key右边的值都大于key，下面用一个例子来理解（希望读者能动手验证）。

 

 

取key=6；

j走到5时,5<6，交换5和i+1，即交换5和10，ij同时后移一位。

j走到3时,3<6，交换3和i+1，即交换3和13，ij同时后移一位。

j走到2时,2<6，交换2和i+1，即交换2和10，ij同时后移一位。

j走到11时,11>6，不用交换，此时j到达数组末尾，交换key和i，即交换6和2。

一趟排序完成，6左边的元素都小于6，右边的元素都大于6。

 

2、左右指针法(非降序)

 之所以叫左右指针，是因为初始的两指针是在数据的两端，看作左右，与前后指针法不同的是两指针是往中间移动的。

①将最右的元素定为key，左指针最左的元素，右指针指向最右的元素。

②右指针向左走，如果遇到了比key小的数，右指针停下，接着左指针往右走，遇到比key大的数时停下。交换左右指针的值，两指针再向中间移一位。

③检查两指针是否重合，不重合时进行②操作，重合时判断key的值与重合位置的值，如果key<重合位置的值，进行交换。

④对两边进行上述操作的递归操作。

（放图说明）

 

取key为5，初始化两指针。

右指针向左移动，到2时2<5,停住。

左指针向右移动，到9时9>5,停住。

交换两指针的值，两指针都向中间移动一位。

两指针相遇，交换key和指针位置的值，至此一趟排序完成。

 

 

3、填坑法（非降序）

 填坑法的坑只有一个，是由指针指向且不断变化的，有些类似于左右指针法，具体不同会在下面分析。

①将数组最右的端定为坑，并记下坑值为key（一趟排序只记这一次），左指针最左的元素，右指针指向最右的元素。

②左指针向右移动，当遇到比坑值大的数时停下，将这个数填入坑中，将左指针此时的位置设为坑。右指针向左移，当遇到比key小的数时，将这个数填入坑中，将右指针此时的位置设为坑。

③判断两指针是否重合，若不重合执行②操作，重合就将初始的key值填入重合的位置。至此一趟排序结束。

（上图中圈圈代表坑）

初始化两指针，将最右端设为坑，并记下其值。

左指针向右移动，一开始就发现7>1，将7填入坑中，左指针停留。

右指针向左移动，一直到7都没有找到比1小的数，这时两指针重合，将key值填入重合位置。

（这只是一种特殊情况，请读者自己作更多的数组来练习）

 

三种方法比较：

指针移动方向：前后指针法比较特别，两指针都是朝一边移动（另外两个方法两指针移动方向不同）。

两指针的完成顺序：左右指针法是两指针都移动到位了，才执行交换，填坑法只要一个指针到位了就执行交换。

两指针的作用：可以说左右指针法和填坑法是相同的。而前后指针法中一个指针决定了插入的位置，一个指针用来检索元素。

最后key值的插入：前后指针法是后指针到头后，交换key值和array[i]（也就是前一个指针指向的值）。左右指针法和填坑法都是在两指针相遇后将key值与指针重合位置的值交换。

 

三、复杂度（要想透彻理解务必看完）

通常情况下，算法在不同情况的复杂度是不同的，对于快排，是否也是这样？下面我将对多种情况下的快排进行分析。

 

1、最优情况

根据快排的分治法思想，每次用key值将数组分为两部分，试想怎样才算是最优情况？

当key值每次都是放在最中间时，数据被分成均匀的两半，这时就出现了最优情况。

让我们看一眼递归树：

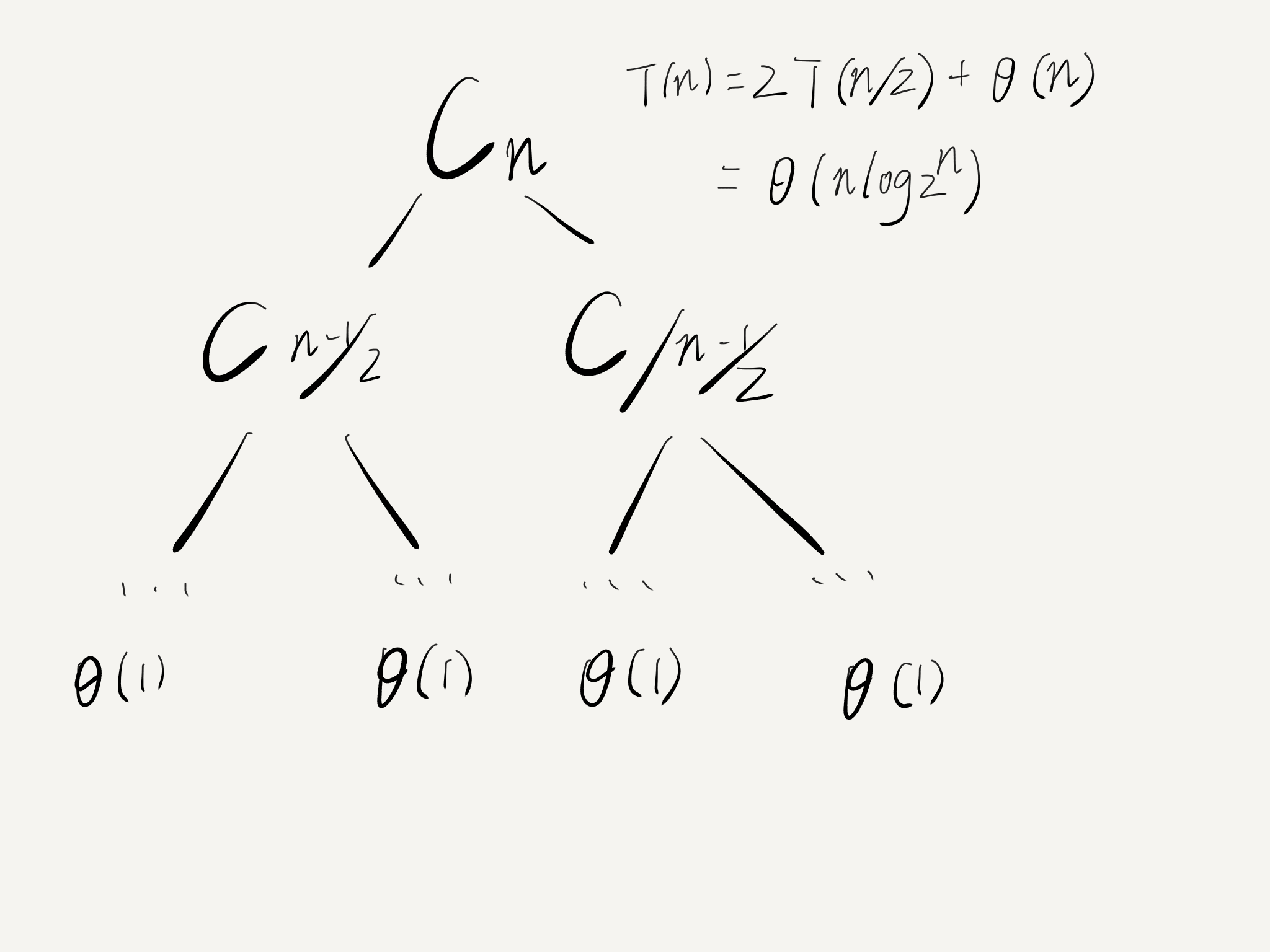
得出在最优情况下快排的复杂度是nlgn

 

2、最坏情况

了解的最优情况，想一下最坏情况的样子吧。

对于一组排序好的数组，我们一般不去验证它是否排好，而是将它重新排一遍。想象一下用快排处理一组已经排好的数据，每次的key值不是最大就是最小，划分的两部分，一部分没有元素，剩下的n-1都在另一部分。这是很糟糕的情况，此时排序的效率大幅降低。

这时快排的复杂度达到了n²（对计算有疑问请在评论区提出）

 

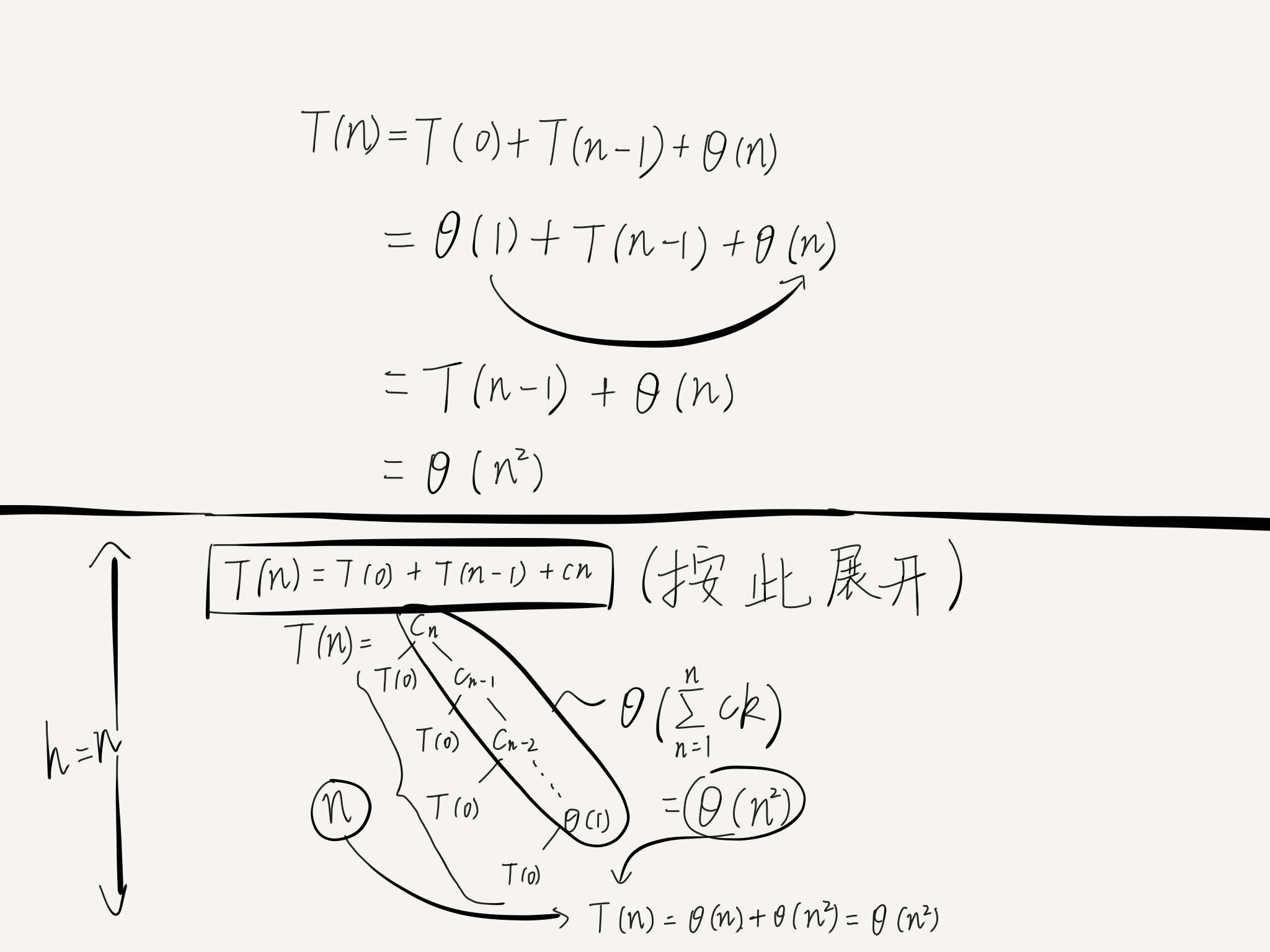
3、固定位置排序

若每次排序key都被放在1/10或9/10的位置呢?请读者参考上面的方式作出分析。

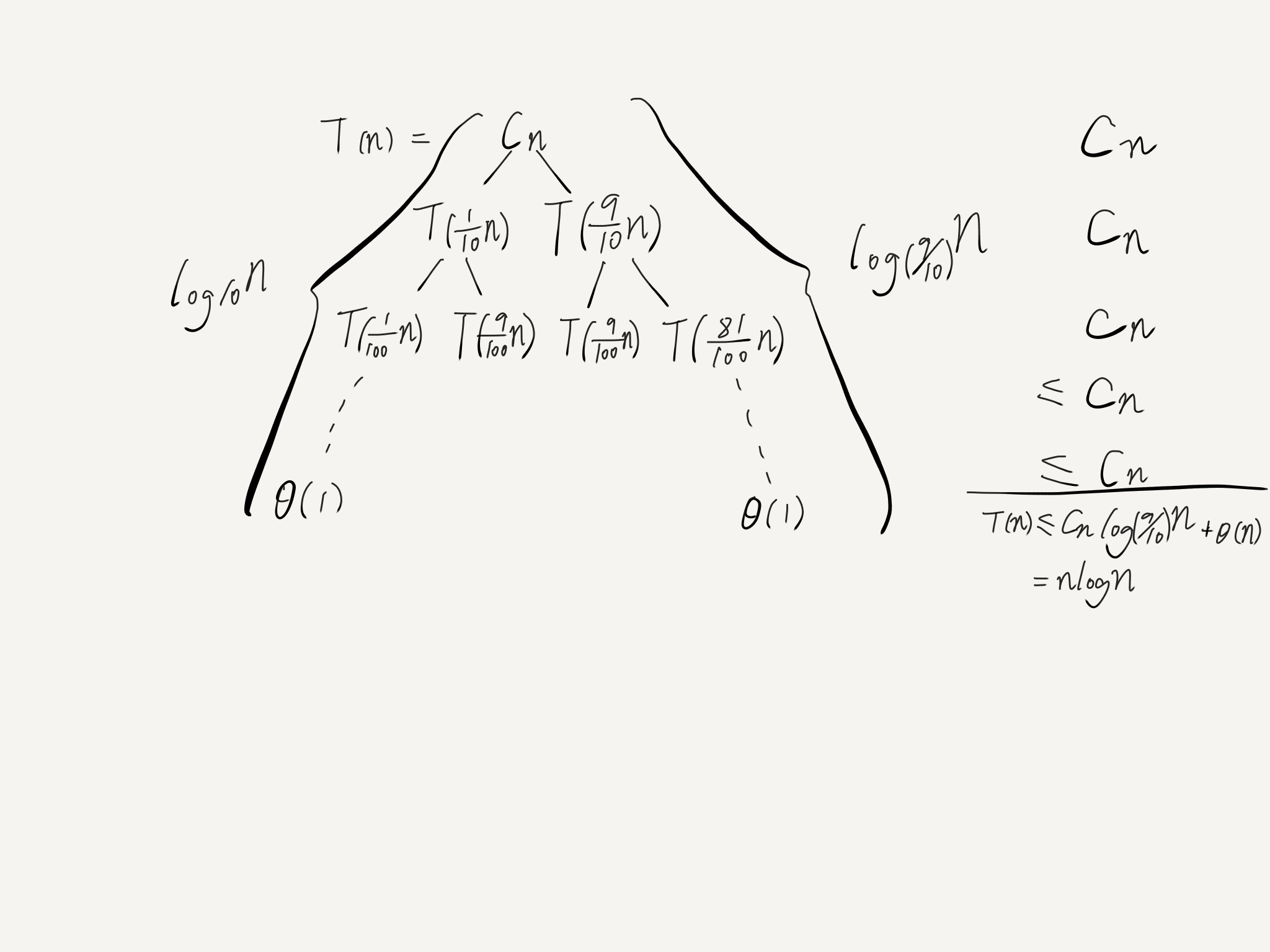
需要注意的是上图标注的两条路径的长度是不一样的（1/10的路径更短），所以在右边每层的相加后面出现小于Cn。

大家应该注意到，在T（n）的算式中没有出现1/10，Cnlog（9/10）n中log（9/10）n代表的是最长路径，Cn是每层的相加，而θ(n) 表示的是所以叶节点。

可以得出即使在固定位置的时候，我们依然是处于最优情况。

 

4、优劣交替排序

发挥想象力，如果在排序时，出现了第一次是最优排序，第二次是最差排序，第三次又回到最优排序...

这时对于整个排序而言，我们到底是在经历最差情况还是最好情况？（请读者在心中给出答案）

利用之前的分析和算式，给出下图：

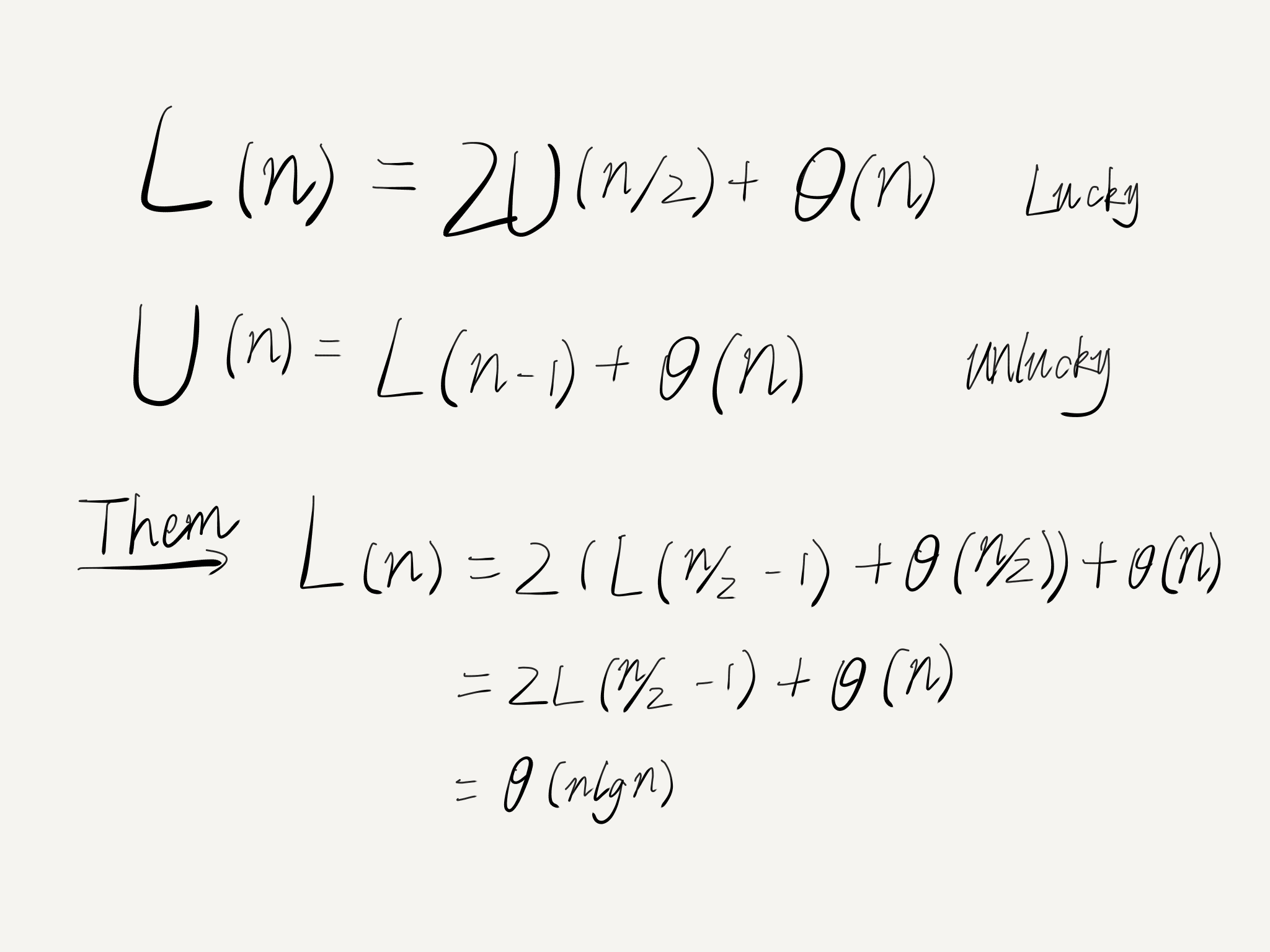
them中的式子用了等价代换（只是将n/2带入U（n））

你猜对了吗，不管猜对与否，你已经对算法有了深刻的认识。除了最坏情况外，快排的复杂度都是一样的。

 

四、算法的优化

鄙人才疏学浅，在这里只提供两个简单的方法供大家参考。算法的思路都很简单，具体的实现在后面代码展示部分。

 

1、三数取中法

在上面的各种情况中，我们不难看出排序的好坏受制于key值，如果我们不选最大或最小的数作为key，那么就可以避开最坏情况，三数取中法就利用了这种思想。

做法：在数组的头、中和尾各取一个元素，将三个数进行比较，选择位于中间的一个数作为key。

 

2、加入插入排序

当排序进行到接近完成时，数组会被分得很小，这时我们可以用一些特定的算法对这些小块排序，插入排序正适用于这种情况（复杂度为O（n²））。

做法：遍历数组，每次将当前元素插入合适的位置。

 

五、代码展示

 

1、前后指针法

#include<iostream>
using namespace std;
#include<assert.h>
int GetMidIndex(int *a,int left,int right);
int PartSort(int *a,int left,int right);
void QuickSort(int *a,int left,int right);
void InsertSort(int* a,int n);
void printArray(int *a,int n);
int main()
{
    int arr[] = { 1, 3, 6, 0, 8, 2, 9, 4, 7, 5 };
    //int arr[] = { 49, 38, 65, 97, 76, 13, 27, 49 };
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "进行快速排序后：";
    QuickSort(arr, 0, n - 1);
    printArray(arr, n);
    system("pause");
    return 0;
}

int GetMidIndex(int *a,int left,int right)
{//三数取中法 
    int max,maxAdress;
    int mid=left+(right-left)/2;
    if(a[left]>=a[mid]){
        max=a[left];
        maxAdress=left;
    }
    else{
        max=a[mid];
        maxAdress=mid;
    }
    if(a[right]>max){
        max=a[right];
        maxAdress=right;
    }
}

int PartSort(int *a,int left,int right)
{//前后指针法的实现 
    int mid=GetMidIndex(a,left,right);
    swap(a[mid],a[left]);
    int key=a[left];
    int j=left+1;
    int i=left;
    while(j<=right&&i<j){
        if(a[j]<key&&++i!=j){
            swap(a[i],a[j]);
        }
        j++;//如果最后一个也比key小，j就会超出数组 
    }
    swap(a[left],a[i]);//交换key值和array[i] 
    return i;    
}

void QuickSort(int *a,int left,int right)
{//快排主要思想（分治法 
    if(left>=right){
        return;
    } 
    if((right-left)<5){
        InsertSort(a,right-left+1);
    }
    int div=PartSort(a,left,right);
    QuickSort(a,left,div-1);
    QuickSort(a,div+1,right);
}

void InsertSort(int* a,int n)//当数组规模较小或者存在多个局部有序的子数组时，算法的执行速度会更快
{//插入排序 每次将一个元素插入以排好的序列 
    for(int i=1;i<n;i++){
        for(int j=i;j>0&&a[j]<a[j-1];j--){
            swap(a[j],a[j-1]);
        }        
    }
}
void printArray(int *a,int n)
{
    for(int i=0;i<n;i++){
        printf("%d ",a[i]);
    }
}

 

2、左右指针法

#include<iostream>
using namespace std;
#include<assert.h>

int PartSort(int* array,int left,int right);
void QuickSort(int* array,int left,int right);
int GetMidIndex(int* a,int left,int right);
void InsertSort(int* a,int n);
void PrintArray(int* a,int n);
int main()//快速排序（填坑法） 
{
    int arr[]={1,4,2,7,8,5,3,9,0,6};
    int n=sizeof(arr)/sizeof(arr[0]);
    QuickSort(arr,0,n-1);
    PrintArray(arr,n);
    system("pause");
    return 0;
}

int PartSort(int* array,int left,int right)
{
    int mid=GetMidIndex(array,left,right);
    swap(array[mid],array[right]);
    int key=array[right];
    while(left<right){//除第一次外，left和right都是从坑开始移动 
        while(left<right&&array[left]<=key){
            ++left;
        }
        array[right]=array[left];
        while(left<right&&array[right]>=key){
            --right;
        }
        array[left]=array[right];
    }
    array[right]=key;
    return right;
}

void QuickSort(int* array,int left,int right)
{//快排核心思想（分治法 
    if(left>=right){
        return;
    }
    if(right-left<=5){
        //printf("insert!");
        InsertSort(array,right-left+1);
    }
    int div=PartSort(array,left,right);
    QuickSort(array,left,div-1);
    QuickSort(array,div+1,right);
} 

void InsertSort(int* a,int n)//当数组规模较小或者存在多个局部有序的子数组时，算法的执行速度会更快
{//插入排序 每次将一个元素插入以排好的序列 
    for(int i=1;i<n;i++){
        for(int j=i;j>0&&a[j]<a[j-1];j--){
            swap(a[j],a[j-1]);
        }        
    }
}

void PrintArray(int* a,int n)
{
    for(int i=0;i<n;i++){
        printf("%d ",a[i]);
    }
}

int GetMidIndex(int *a,int left,int right)
{//三数取中法（序列是正序或者逆序时，每次选到的枢轴都是没有起到划分的作用。快排的效率会极速退化。 
    assert(a);
    int max,maxAdress;
    int mid=left+(right-left)/2;
    if(a[left]<=a[right]){
        if(a[mid]<a[left]){
            return left;
        }
        else if(a[mid]>a[right]){
            return right;
        }
        else{
            return mid;
        }
    }
    else{
        if(a[mid]<a[right]){
            return right; 
        }
        else if(a[mid]>a[left]){
            return left;
        }
        else{
            return mid;
        }
    }
}

 

3、填坑法

#include<iostream>
using namespace std;
#include<assert.h>

int PartSort(int* array,int left,int right);
void QuickSort(int* array,int left,int right);
int GetMidIndex(int* a,int left,int right);
void PrintArray(int* a,int n);
int main()//快速排序（填坑法） 
{
    int arr[]={1,4,2,7,8,5,3,9,0,6};
    int n=sizeof(arr)/sizeof(arr[0]);
    QuickSort(arr,0,n-1);
    PrintArray(arr,n);
    system("pause");
    return 0;
}

int PartSort(int* array,int left,int right)
{
    int mid=GetMidIndex(array,left,right);
    swap(array[mid],array[right]);
    int key=array[right];
    while(left<right){//除第一次外，left和right都是从坑开始移动 
        while(left<right&&array[left]<=key){
            ++left;
        }
        array[right]=array[left];
        while(left<right&&array[right]>=key){
            --right;
        }
        array[left]=array[right];
    }
    array[right]=key;
    return right;
}

void QuickSort(int* array,int left,int right)
{
    if(left>=right){
        return;
    }
    int div=PartSort(array,left,right);
    QuickSort(array,left,div-1);
    QuickSort(array,div+1,right);
} 

void PrintArray(int* a,int n)
{
    for(int i=0;i<n;i++){
        printf("%d ",a[i]);
    }
}

int GetMidIndex(int *a,int left,int right)
{//三数取中法（序列是正序或者逆序时，每次选到的枢轴都是没有起到划分的作用。快排的效率会极速退化。 
    assert(a);
    int max,maxAdress;
    int mid=left+(right-left)/2;
    if(a[left]<=a[right]){
        if(a[mid]<a[left]){
            return left;
        }
        else if(a[mid]>a[right]){
            return right;
        }
        else{
            return mid;
        }
    }
    else{
        if(a[mid]<a[right]){
            return right; 
        }
        else if(a[mid]>a[left]){
            return left;
        }
        else{
            return mid;
        }
    }
}