【学习笔记】遗传算法求解单元函数最值问题
前言
在网上找了很久的关于遗传算法的讲解,但是大多都讲的不是很清楚,好不容易找到一篇讲得比较好的,然后算法的正确性又不高……蒟蒻今天根据自己的理解,整理了以下关于遗传算法的一些讲解。
算法讲解
aee092b9-d84e-4028-863d-9534d16e444d
一、定义
- ChatGPT给出的解释: 遗传算法是一种启发式优化算法,利用生物进化中的“选择、交叉和变异”操作,通过不断的迭代来寻找最优解。该算法由Holland在60年代发明,通过模拟自然选择的过程,将解搜索空间中的“个体”进行随机化、交叉和变异,以产生新的解,并筛选出适应度高的解作为“种群”,直至找到最优解为止。
- 百度百科: 遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
- 个人的理解: 通过对于种群(即我们需要求解的自变量)进行人为地筛选、交叉、变异,从而得到一个适应度最高(求得的函数值最优)的种群,进而得到问题的最优解。翻译成人话就是对于一堆数据不断地挑选最优地那一部分,然后改变这些数据中的一部分,然后重复多次,得到你想要的结果。
二、和生物学的一些联系
如图:

这是一个 DNA 分子的片段,那么我们把它拉直之后就可以得到这样一个结构:
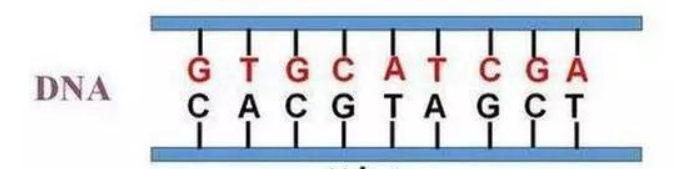
其中每个字母都记录了一些生命体的信息,那么我们如果考虑只有两种模式即

我们怎么用这个串来表示我们想要求得的数呢?显然,一个上面的
好了,这样我们就可以使用一个基因(
三、遗传算法的步骤
遗传算法基本上都可以分成如下几步:
- 随机生成大量的相同长度的基因;
- 为每个个体分配相同数量的基因,其中,每个个体分配到的基因的数量即为函数中自变量的个数,因为这里讲的是单元函数,那么每个个体中只含一条基因,这也是遗传算法最简单的形式;
- 将指定数目的个体放置在一起形成初始种群;
- 对初始种群进行筛选,我这里选择了轮盘赌法;
- 对于种群进行交叉,即两个个体之间出现基因片段的交换;
- 对于种群进行变异,即使某些个体的某个基因发生突变,可以简单理解为
- 不断重复以上步骤,知道得到误差范围内的最优解或迭代次数用尽,在这里,迭代一次包括了一次筛选、种群的交叉、种群的变异。
四、随机生成每个个体的基因
首先,我们需要确定基因的长度。用二进制来表示一个浮点数实在是太不方便了,那么有没有什么更简单一点的方法呢?假设我们的函数的定义域为
那么,我们的每个小区间的长度具体应该是多少呢?显然,对于每个函数求值问题,题目中都会给出精度要求,假设这里我们的精度为
好了,现在我们已经知道基因的长度和步长了,那么我们可以得到,我们实际的
inline void Rand(int *res){
for(register int i=0;i<GEN_LENGTH;++i){
int x=(rand()%2);
res[i]=(int)x;
}
} 那么,我们在计算
//根据二进制计算出实际所对应的数
inline double GetNumVal(int *Gen,double LR,double STEP){
long double x=0;
for(register int i=0;i<GEN_LENGTH;++i)
x=x*2.0+(double)Gen[i];
double Dis=x*STEP;
return LR+Dis;
}
这里也顺便放一下计算基因长度的代码和计算步长的代码。
计算基因长度的代码:
//计算基因长度
inline int GetGenLen(double LR,double RR){
double Delta=(RR-LR);
double Up=Delta/MaxExp;
double LEN=log(2.0,Up);
return (int) ceil(LEN);
}计算步长的代码:
//快速幂
template<typename T>
inline T Pow(T x,T n){
T res=1;
while(n){
if(n&1) res=res*x;
x=x*x;n=n>>1;
}return res;
}
//计算步长
inline double GetStep(double LR,double RR,int Len){
double Delta=(RR-LR);
double POW=Pow(2,Len);
POW=POW - (double)(1);
double STEP=Delta/POW;
return STEP;
}五、生成个体并生成第一代种群
因为这里每个个体只含有一条基因,那么我们直接按照上面所说的方法就行了。
构建初始种群的时候,我们需要首先确定种群的大小,通常这个值一般在
当我们选择好种群大小之后,我们可以定义一个数组,用来存储我们的个体,那么这个数组,也就是我们的种群了。
六、筛选种群
这里我一般选择的是轮盘赌算法,网上对于这个算法已经有很好的讲解了(博客),所以这里只简单介绍一下。
轮盘赌算法的核心在于,它让当前的较劣解也有概率被选中,而较优解也有概率被淘汰,不过概率很小,这就使得种群能够拥有较大的变化率,也更不容易陷入一个局部最优解中。
大体思路如下:
- 根据适应度函数计算每一个个体的适应度;
- 按照适应度的大小为每个个体分配被选择的概率;
- 计算概率的前缀和,得到一个概率区间;
- 得到一个
计算适应度函数的方法如下:
- 根据基因计算出
- 找到这个种群中
- 如果是求函数最大值的话,那么这个个体的适应度即为
计算每个个体被选中的概率的方式如下:
- 计算出这个种群中所有个体的适应度之和
- 每个个体被选中的概率即为
判断当前的小数值位于哪一个区间内:
这里有两种方法。第一种是比较常见且误差较小但是速度较慢的暴力枚举法,即从第一个区间开始,依次枚举判断是否位于这个区间内;第二种是使用二分,这个方法速度较快但是因为精度问题可能会存在误判的问题,目前我也没有找到什么比较好的解决方法,但是其实对于结果的影响并不大,因为只有较小的概率判断出错,而因为轮盘赌本身就是一个随机算法,所以可以忽略这个影响。
好了,现在我们已经学会轮盘赌算法了,那么我们就可以使用它来筛选种群了。注意,这里对种群的筛选只是提高较优解的比重同时降低较劣解的比重,并不会改变种群的大小,因此,我们需要选择和种群大小一样的次数,可以考虑使用一个数组来存储被选到的个体,最终把这个数组复制给我们的种群就可以了。
七、两个个体的交叉
这里,我们首先需要需要确定一个交叉概率
交叉的本质是发生了基因片段的交换,对于每一个个体大体步骤如下:
- 得到一个
- 随机选择一个与该个体发生交叉的个体;
- 进行基因的互换。
基因互换有两种方式,第一种是直接交换两个个体基因的后半段,第二种是基因从前往后每一位都有可能发生交换,但是概率从前往后依次降低。我们可以选择第一种或第二种或随机选择一种方法。因为我们的基因是存在一个数组里的,那么我们直接用 swap 来按位交换即可。
八、基因的变异
与个体的交叉一样,我们需要先确定一个变异概率
对于每个个体,都可能发生变异,步骤如下:
- 得到一个
- 随机选择这个个体的一位基因,并替换为相反数;
因为使用数组存储的基因,那么我们直接把当前这一位
九、多次迭代
同上,我们需要确定一个迭代次数
通常,迭代可能会因为两种情况结束:
- 已经得到了最优解;
- 迭代次数用尽;
如上所讲,在每次迭代的过程中,我们需要对于当前的种群进行筛选,并对于每个个体一定概率发生交叉,一定概率发生变异。
十、遗传算法的整体流程
如图:

十一、遗传算法的优缺点
优点:
- 能够在较短的时间内得到一个很优的近似解;
- 拓展性强,可以用于多种问题的求解;
- 能够在较大数据范围时保持较高精度
- 简单易懂。
缺点:
- 精确度不够高,答案波动大;
- 容易在变异和交叉的过程中失去最优解;
- 算法码量较大(也许是我自己的问题);
- 效率较低。
十二、遗传算法的优化
这里总结了两个比较常用的优化方法:
- 父辈优化:即对新产生的个体与父辈进行比较,如果没有父辈优,那么不适用它替换父辈;
- 保留精英策略:将父辈中优秀的基因直接复制给后代。
以下是一些我个人的一些优化方法(借用了一些模拟退火的思想):
- 每次迭代后记录这一代的最优解,可以保证最优解不会被淘汰;
- 建立多个种群,得到的最优解即为所有种群的最优解,可以避免某些种群陷入局部最优解中,虽然会一定程度上降低算法的效率,但是能够使得得到的解更加逼近最优解。
例题&讲解
题目描述
已知一个函数
不难发现,这是一个偶函数,借助一些数学工具,我们可以求出当
那么,按照遗传算法的步骤,我们就可以确定基因长度为 new int 动态分配内存。
为了方便对于个体的初始化、适应度的计算,我们可以将每个个体定义为一个结构体,这个结构体主要包含:一个指针,用来存储基因;一个浮点数 init(),初始化个体;GetFit(),计算个体适应度;GetPro(),计算个体被选择的概率。具体代码如下:
//构建种族个体
struct RACE{
//这里只有一条基因
int *gen;
//个体的适应度
double Fit;
//个体被选择的概率
double Probability;
//初始化
inline void init(){
gen=new int[GEN_LENGTH];
for(register int i=0;i<GEN_LENGTH;++i)
gen[i]=0;
}
//获取个体的适应度
inline void GetFit(){
double x=GetNumVal(gen,LRange,Step);
Fit = f(x); return;
}
inline void GetFit(double MinFit,double MaxFit){
double Delta1=Fit-MinFit;
double Delta2=MaxFit-MinFit;
Fit=Delta1/Delta2;
}
//获取个体被选择的概率
inline void GetPro(double SumFit){
Probability=Fit/SumFit;
}
};接下来是对于每个个体的基因的初始化,直接按照之前所讲的方法进行就可以了,代码如下:
inline void Rand(int *res){
for(register int i=0;i<GEN_LENGTH;++i){
int x=(rand()%2);
res[i]=(int)x;
}
}
//初始化得到第一代种群
inline void InitRace(){
//循环遍历得到每一个第一代个体
for(register int i=0;i<Population;++i){
//将每个个体被选择的概率初始化为0
a[i].Probability=0.0;
//将每个个体的基因赋为随机值
Rand(a[i].gen);
//获取每个个体的适应度
a[i].GetFit();
}
}然后我们就可以对初始种群进行筛选了。首先我们需要计算出每个个体的适应度和被选择的概率,同时预处理出概率的前缀和,这一部分上面已经讲过了,在此不过多阐述。代码如下:
//获取每个个体的适应度
for(register int i=0;i<Population;++i){
a[i].GetFit();
//记录当前的最优个体
if(a[i].Fit>ans){
ans=a[i].Fit;
ansx=GetNumVal(a[i].gen,LRange,Step);
}
}
//获取最大和最小适应度
double Mint=1e18,Maxt=1e-18;
for(register int i=0;i<Population;++i){
if(a[i].Fit<Mint) Mint=a[i].Fit;
if(a[i].Fit>Maxt) Maxt=a[i].Fit;
}
//根据最大和最小适应度来计算当前个体的适应度
//即,将每个个体的函数值适应度转化为相对适应度
if(Mint==Maxt)
for(register int i=0;i<Population;++i)
a[i].Fit=1.0/(double)Population;
else
for(register int i=0;i<Population;++i)
a[i].GetFit(Mint,Maxt);
//计算适应度之和
double SumFit=0;
for(register int i=0;i<Population;++i)
SumFit=SumFit+a[i].Fit;
//计算每个个体被选择的概率
for(register int i=0;i<Population;++i)
a[i].GetPro(SumFit);
//计算概率前缀和
for(register int i=0;i<Population;++i){
if(i==0) RangePro[i]=a[i].Probability;
else RangePro[i]=RangePro[i-1]+a[i].Probability;
}为了方便存储被选中的个体,我们创建了一个 vector 数组
inline int Lower(double x){
double now=0.0;int pos=0;
int res=0;
for(register int i=7;i>=0;--i){
if(pos+(1<<i)>=Population)
continue;
int nxt=pos+(1<<i);
if(now+RangePro[nxt]>=x)
res=nxt;
if(now+RangePro[nxt]<x)
now+=RangePro[nxt],pos=nxt;
}return res;
} 选择个体代码如下:
for(register int i=1;i<=Population;++i){
double Pro=RAND();
//第pos个个体被选择
//使用倍增加快查找速度
//可能会有一定的误差但是影响不大
int pos=Lower(Pro);
Choose.push_back(a[pos]);
}
//将新得到的种群替换原来的种群
for(register int i=0;i<Population;++i)
a[i]=Choose[i];轮盘赌算法选择个体完整代码如下:
//获取每个个体的适应度
for(register int i=0;i<Population;++i)
a[i].GetFit();
//获取最大和最小适应度
double Mint=1e18,Maxt=1e-18;
for(register int i=0;i<Population;++i){
if(a[i].Fit<Mint) Mint=a[i].Fit;
if(a[i].Fit>Maxt) Maxt=a[i].Fit;
}
//根据最大和最小适应度来计算当前个体的适应度
//即,将每个个体的函数值适应度转化为相对适应度
if(Mint==Maxt)
for(register int i=0;i<Population;++i)
a[i].Fit=1.0/(double)Population;
else
for(register int i=0;i<Population;++i)
a[i].GetFit(Mint,Maxt);
//计算适应度之和
double SumFit=0;
for(register int i=0;i<Population;++i)
SumFit=SumFit+a[i].Fit;
//计算每个个体被选择的概率
for(register int i=0;i<Population;++i)
a[i].GetPro(SumFit);
//计算概率前缀和
for(register int i=0;i<Population;++i){
if(i==0) RangePro[i]=a[i].Probability;
else RangePro[i]=RangePro[i-1]+a[i].Probability;
}
//用vector存储选择的个体
std::vector<RACE> Choose;
//轮盘赌算法选择个体
//使得种群的大小不变化
//但是更优个体的比重增加
for(register int i=1;i<=Population;++i){
double Pro=RAND();
//第pos个个体被选择
//使用倍增加快查找速度
//可能会有一定的误差但是影响不大
int pos=Lower(Pro);
Choose.push_back(a[pos]);
}
//将新得到的种群替换原来的种群
for(register int i=0;i<Population;++i)
a[i]=Choose[i];接下来需要考虑每个个体是否会与其他的个体发生交叉,交换基因片段,因为不是很清楚两种交换基因的方式哪个更好,于是选择了随机选择一种交换基因的方式,这一部分代码如下:
发生基因片段的交换
//每个个体都有可能发生
for(register int i=0;i<Population;++i){
double Pro=RAND();
//只有当当前的随机值小于交换概率时
//才会发生基因片段的交换
if(Pro>=CrossRate) continue;
//获取和当前个体发生基因交换的个体
int other=rand()%Population;
//有两种交换方法
int kinds=rand()%2;
if(!kinds){//按照从前往后概率依次降低交换
for(register int j=0;j<GEN_LENGTH;++j){
double Prob=1.0/(double)(j+1);
double NowPro=RAND();
if(NowPro>Prob) continue;
std::swap(a[i].gen[j],a[other].gen[j]);
}
}else{//后面一半完全交换
for(register int j=GEN_LENGTH/2;j<GEN_LENGTH;++j)
std::swap(a[i].gen[j],a[other].gen[j]);
}
}最后就是变异了,其实变异很简单,只需要判断是否会发生变异,然后随机修改某一位基因即可,代码:
//变异
for(register int i=0;i<Population;++i){
double NowPro=RAND();
if(NowPro>=MutationRate)
continue;
int pos=rand()%GEN_LENGTH;
a[i].gen[pos]=a[i].gen[pos]^1;
}当然了,我们每迭代一次还需要记录当前这一代的最优解,避免最优个体在某次迭代中被淘汰。
for(register int i=0;i<Population;++i){
//记录当前的最优个体
if(a[i].Fit>ans){
ans=a[i].Fit;
ansx=GetNumVal(a[i].gen,LRange,Step);
}
}运行一下可以发现,不同的种群得到的最优解是不一样的,有的时候甚至会有极大的误差。但是每个种群的演变方向是我们不能预测和控制的,那么我们能做的就是多生成几个种群,然后找到这些种群中最优个体最优的那一个。这里的 work() 也就是得到一个种群的最优解。
for(register int i=1;i<=200;++i)
work();最终,我们程序运行得到的
#include<math.h>
#include<time.h>
#include<stdio.h>
#include<algorithm>
#define ll long long
//最多迭代150代
const int MAX_GENOR=150;
//初始种群大小
const int Population=100;
//基因长度
int GEN_LENGTH;
//步长
//当前的基因转换为十进制后的值
//乘以步加上左端点等于
//实际的数值
double Step;
//交叉率
const double CrossRate=0.9;
//变异率
const double MutationRate=0.148;
//范围左端点
const double LRange=-1;
//范围右端点
const double RRange=2;
//要求的精度误差
const double MaxExp=1e-6;
//确定一个Π的值
const double Pi=3.1415926536;
//重写log函数
inline double log(double m,double n){
double Uppe=log(n);
double Down=log(m);
return Uppe/Down;
}
//快速幂
template<typename T>
inline T Pow(T x,T n){
T res=1;
while(n){
if(n&1) res=res*x;
x=x*x;n=n>>1;
}return res;
}
//计算基因长度
inline int GetGenLen(double LR,double RR){
double Delta=(RR-LR);
double Up=Delta/MaxExp;
double LEN=log(2.0,Up);
return (int) ceil(LEN);
}
//计算步长
inline double GetStep(double LR,double RR,int Len){
double Delta=(RR-LR);
double POW=Pow(2,Len);
POW=POW - (double)(1);
double STEP=Delta/POW;
return STEP;
}
//根据二进制计算出实际所对应的数
inline double GetNumVal(int *Gen,double LR,double STEP){
long double x=0;
for(register int i=0;i<GEN_LENGTH;++i)
x=x*2.0+(double)Gen[i];
double Dis=x*STEP;
return LR+Dis;
}
//根据给定函数计算当前x的函数值
inline double f(double x){
return x*sin(10*Pi*x)+1.0;
}
//构建种族个体
struct RACE{
//这里只有一条基因
int *gen;
//个体的适应度
double Fit;
//个体被选择的概率
double Probability;
//初始化
inline void init(){
gen=new int[GEN_LENGTH];
for(register int i=0;i<GEN_LENGTH;++i)
gen[i]=0;
}
//获取个体的适应度
inline void GetFit(){
double x=GetNumVal(gen,LRange,Step);
Fit = f(x); return;
}
inline void GetFit(double MinFit,double MaxFit){
double Delta1=Fit-MinFit;
double Delta2=MaxFit-MinFit;
Fit=Delta1/Delta2;
}
//获取个体被选择的概率
inline void GetPro(double SumFit){
Probability=Fit/SumFit;
}
};
//定义一个初始化种群
RACE a[Population];
//存储区间概率
double RangePro[Population];
//返回一个随机的指针
inline void Rand(int *res){
for(register int i=0;i<GEN_LENGTH;++i){
int x=(rand()%2);
res[i]=(int)x;
}
}
//初始化得到第一代种群
inline void InitRace(){
//循环遍历得到每一个第一代个体
for(register int i=0;i<Population;++i){
//将每个个体被选择的概率初始化为0
//方便之后的淘汰
a[i].Probability=0.0;
//将每个个体的基因赋为随机值
Rand(a[i].gen);
//获取每个个体的适应度
a[i].GetFit();
}
}
//产生一个0~1的随机数
inline double RAND(){
double fez=rand();
double fem=RAND_MAX;
return fez/fem;
}
double ans=-1e18,ansx;
inline int Lower(double x){
double now=0.0;int pos=0;
int res=0;
for(register int i=7;i>=0;--i){
if(pos+(1<<i)>=Population)
continue;
int nxt=pos+(1<<i);
if(now+RangePro[nxt]>=x)
res=nxt;
if(now+RangePro[nxt]<x)
now+=RangePro[nxt],pos=nxt;
}return res;
}
//对于每一代进行筛选和繁殖
inline void GA(){
//获取每个个体的适应度
for(register int i=0;i<Population;++i){
a[i].GetFit();
//记录当前的最优个体
if(a[i].Fit>ans){
ans=a[i].Fit;
ansx=GetNumVal(a[i].gen,LRange,Step);
}
}
//获取最大和最小适应度
double Mint=1e18,Maxt=1e-18;
for(register int i=0;i<Population;++i){
if(a[i].Fit<Mint) Mint=a[i].Fit;
if(a[i].Fit>Maxt) Maxt=a[i].Fit;
}
//根据最大和最小适应度来计算当前个体的适应度
//即,将每个个体的函数值适应度转化为相对适应度
if(Mint==Maxt)
for(register int i=0;i<Population;++i)
a[i].Fit=1.0/(double)Population;
else
for(register int i=0;i<Population;++i)
a[i].GetFit(Mint,Maxt);
//计算适应度之和
double SumFit=0;
for(register int i=0;i<Population;++i)
SumFit=SumFit+a[i].Fit;
//计算每个个体被选择的概率
for(register int i=0;i<Population;++i)
a[i].GetPro(SumFit);
//计算概率前缀和
for(register int i=0;i<Population;++i){
if(i==0) RangePro[i]=a[i].Probability;
else RangePro[i]=RangePro[i-1]+a[i].Probability;
}
//用vector存储选择的个体
std::vector<RACE> Choose;
//轮盘赌算法选择个体
//使得种群的大小不变化
//但是更优个体的比重增加
for(register int i=1;i<=Population;++i){
double Pro=RAND();
//第pos个个体被选择
//使用倍增加快查找速度
//可能会有一定的误差但是影响不大
int pos=Lower(Pro);
Choose.push_back(a[pos]);
}
//将新得到的种群替换原来的种群
for(register int i=0;i<Population;++i)
a[i]=Choose[i];
//发生基因片段的交换
//每个个体都有可能发生
for(register int i=0;i<Population;++i){
double Pro=RAND();
//只有当当前的随机值小于交换概率时
//才会发生基因片段的交换
if(Pro>=CrossRate) continue;
//获取和当前个体发生基因交换的个体
int other=rand()%Population;
//有两种交换方法
int kinds=rand()%2;
if(!kinds){//按照从前往后概率依次降低交换
for(register int j=0;j<GEN_LENGTH;++j){
double Prob=1.0/(double)(j+1);
double NowPro=RAND();
if(NowPro>Prob) continue;
std::swap(a[i].gen[j],a[other].gen[j]);
}
}else{//后面一半完全交换
for(register int j=GEN_LENGTH/2;j<GEN_LENGTH;++j)
std::swap(a[i].gen[j],a[other].gen[j]);
}
}
//变异
for(register int i=0;i<Population;++i){
double NowPro=RAND();
if(NowPro>=MutationRate)
continue;
int pos=rand()%GEN_LENGTH;
a[i].gen[pos]=a[i].gen[pos]^1;
}
}
inline void work(){
//初始化基因长度
GEN_LENGTH=GetGenLen(LRange,RRange);
//计算每步步长
Step=GetStep(LRange,RRange,GEN_LENGTH);
for(register int i=0;i<Population;++i)
a[i].init();
InitRace();//初始化种群
for(register int i=1;i<=MAX_GENOR;++i)
GA();
}signed main(){
srand(114514);srand(rand());srand(time(0));
for(register int i=1;i<=200;++i) work();
printf("When x=%.18lf,f(x) have the bigest num,",ansx);
printf("it's %.18lf",ans);
}好了,这道题你已经听懂了,那么,如果将问题修改为求
代码如下:
#include<math.h>
#include<time.h>
#include<stdio.h>
#include<algorithm>
#define ll long long
//最多迭代150代
const int MAX_GENOR=150;
//初始种群大小
const int Population=100;
//基因长度
int GEN_LENGTH;
//步长
//当前的基因转换为十进制后的值
//乘以步加上左端点等于
//实际的数值
double Step;
//交叉率
const double CrossRate=0.78;
//变异率
const double MutationRate=0.148;
//范围左端点
const double LRange=-1;
//范围右端点
const double RRange=2;
//要求的精度误差
const double MaxExp=1e-7;
//确定一个Π的值
const double Pi=3.1415926536;
//重写log函数
inline double log(double m,double n){
double Uppe=log(n);
double Down=log(m);
return Uppe/Down;
}
//快速幂
template<typename T>
inline T Pow(T x,T n){
T res=1;
while(n){
if(n&1) res=res*x;
x=x*x;n=n>>1;
}return res;
}
//计算基因长度
inline int GetGenLen(double LR,double RR){
double Delta=(RR-LR);
double Up=Delta/MaxExp;
double LEN=log(2.0,Up);
return (int) ceil(LEN);
}
//计算步长
inline double GetStep(double LR,double RR,int Len){
double Delta=(RR-LR);
double POW=Pow(2,Len);
POW=POW - (double)(1);
double STEP=Delta/POW;
return STEP;
}
//根据二进制计算出实际所对应的数
inline double GetNumVal(int *Gen,double LR,double STEP){
long double x=0;
for(register int i=0;i<GEN_LENGTH;++i)
x=x*2.0+(double)Gen[i];
double Dis=x*STEP;
return LR+Dis;
}
//根据给定函数计算当前x的函数值
inline double f(double x){
return x*sin(10*Pi*x)+1.0;
}
//构建种族个体
struct RACE{
//这里只有一条基因
int *gen;
//个体的适应度
double Fit;
//个体被选择的概率
double Probability;
//初始化
inline void init(){
gen=new int[GEN_LENGTH];
for(register int i=0;i<GEN_LENGTH;++i)
gen[i]=0;
}
//获取个体的适应度
inline void GetFit(){
double x=GetNumVal(gen,LRange,Step);
Fit = f(x); return;
}
inline void GetFit(double MinFit,double MaxFit){
double Delta1=MaxFit-Fit;
double Delta2=MaxFit-MinFit;
Fit=Delta1/Delta2;
}
//获取个体被选择的概率
inline void GetPro(double SumFit){
Probability=Fit/SumFit;
}
};
//定义一个初始化种群
RACE a[Population];
//存储区间概率
double RangePro[Population];
//返回一个随机的指针
inline void Rand(int *res){
for(register int i=0;i<GEN_LENGTH;++i){
int x=(rand()%2);
res[i]=(int)x;
}
}
//初始化得到第一代种群
inline void InitRace(){
//循环遍历得到每一个第一代个体
for(register int i=0;i<Population;++i){
//将每个个体被选择的概率初始化为0
//方便之后的淘汰
a[i].Probability=0.0;
//将每个个体的基因赋为随机值
Rand(a[i].gen);
//获取每个个体的适应度
a[i].GetFit();
}
}
//产生一个0~1的随机数
inline double RAND(){
double fez=rand();
double fem=RAND_MAX;
return fez/fem;
}
double ans=1e18,ansx;
inline int Lower(double x){
double now=0.0;int pos=0;
int res=0;
for(register int i=7;i>=0;--i){
if(pos+(1<<i)>=Population)
continue;
int nxt=pos+(1<<i);
if(now+RangePro[nxt]>=x)
res=nxt;
if(now+RangePro[nxt]<x)
now+=RangePro[nxt],pos=nxt;
}return res;
}
//对于每一代进行筛选和繁殖
inline void GA(int PPP){
//获取每个个体的适应度
for(register int i=0;i<Population;++i){
a[i].GetFit();
//记录当前的最优个体
if(a[i].Fit<ans){
ans=a[i].Fit;
ansx=GetNumVal(a[i].gen,LRange,Step);
}
}
//获取最大和最小适应度
double Mint=1e18,Maxt=1e-18;
for(register int i=0;i<Population;++i){
if(a[i].Fit<Mint) Mint=a[i].Fit;
if(a[i].Fit>Maxt) Maxt=a[i].Fit;
}
//根据最大和最小适应度来计算当前个体的适应度
//即,将每个个体的函数值适应度转化为相对适应度
if(Mint==Maxt)
for(register int i=0;i<Population;++i)
a[i].Fit=1.0/(double)Population;
else
for(register int i=0;i<Population;++i)
a[i].GetFit(Mint,Maxt);
//计算适应度之和
double SumFit=0;
for(register int i=0;i<Population;++i)
SumFit=SumFit+a[i].Fit;
//计算每个个体被选择的概率
for(register int i=0;i<Population;++i)
a[i].GetPro(SumFit);
//计算概率前缀和
for(register int i=0;i<Population;++i){
if(i==0) RangePro[i]=a[i].Probability;
else RangePro[i]=RangePro[i-1]+a[i].Probability;
}
//轮盘赌算法选择个体
//使得种群的大小不变化
//但是更优个体的比重增加
//用vector存储选择的个体
std::vector<RACE> Choose;
for(register int i=1;i<=Population;++i){
double Pro=RAND();
//第pos个个体被选择
//使用二分加快查找速度
//可能会有一定的误差但是影响不大
int pos=Lower(Pro);
Choose.push_back(a[pos]);
}
//将新得到的种群替换原来的种群
for(register int i=0;i<Population;++i)
a[i]=Choose[i];
//发生基因片段的交换
//每个个体都有可能发生
for(register int i=0;i<Population;++i){
double Pro=RAND();
//只有当当前的随机值小于交换概率时
//才会发生基因片段的交换
if(Pro>=CrossRate) continue;
//获取和当前个体发生基因交换的个体
int other=rand()%Population;
//有两种交换方法
int kinds=rand()%3;
if(!kinds){//按照从前往后概率依次降低交换
for(register int j=0;j<GEN_LENGTH;++j){
double Prob=1.0/(double)(j+1);
double NowPro=RAND();
if(NowPro>Prob) continue;
std::swap(a[i].gen[j],a[other].gen[j]);
}
}else{//后面一半完全交换
for(register int j=GEN_LENGTH/2;j<GEN_LENGTH;++j)
std::swap(a[i].gen[j],a[other].gen[j]);
}
}
//变异
for(register int i=0;i<Population;++i){
double NowPro=RAND();
if(NowPro>=MutationRate)
continue;
int pos=rand()%GEN_LENGTH;
a[i].gen[pos]=a[i].gen[pos]^1;
}
}
inline void work(int PPP){
//初始化基因长度
GEN_LENGTH=GetGenLen(LRange,RRange);
//计算每步步长
Step=GetStep(LRange,RRange,GEN_LENGTH);
for(register int i=0;i<Population;++i)
a[i].init();
InitRace();//初始化种群
printf("%d\n",PPP);
for(register int i=1;i<=MAX_GENOR;++i)
GA(i);
printf("%d\n",PPP);
}signed main(){
srand(114514);
srand(rand());
srand(time(0));
for(register int i=1;i<=200;++i)
work(i);
printf("When x=%.18lf,f(x) have the bigest num,",ansx);
printf("it's %.18lf",ans);
}鸣谢&声明
本文对于文章一文看懂遗传算法【c/c++实现】多有借鉴(指图片和文章格式),并选取了同样的例题来进行讲解。
因为这篇博文的作者的代码在稳定性和精确度上还有待提高,最终计算出的答案和正确答案有较大误差(虽然我也只精确到了小数点后第九位),所以蒟蒻选择再讲一次这道题,也算是对于该文章的补充。
内容也均为我自己对于这个算法的理解,如有部分相似,望作者见谅。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【.NET】调用本地 Deepseek 模型
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· DeepSeek “源神”启动!「GitHub 热点速览」
· 我与微信审核的“相爱相杀”看个人小程序副业
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库