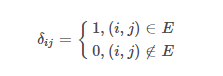浅浅记录学习情况叭

Basic Concepts

1. 对于一个给定的网络G=(V,E),其中V为网络的节点集,E为网络的边集.
2. Trace(迹): 将G划分为q个社区,我们用一个qxq的对称矩阵e来表示该划分,e中的每个元素表示连接社区i与社区j的边在G的全部边中所占的比例显然有∑_i,je_ij=1。矩阵e的迹Tr(e)表示连接社区内部节点的边的占比，一个好的社区划分应该有一个数值很高的迹。
3. k_in,k_out分别代表社区总的的内部度与外部度。社区的内部度等于社区内部链接数的两倍，外部度是社区的每个成员与图的其余部分的链接数。

Algorithm_cluster detection

1.不重叠聚类算法

层次聚类

1. GN algorithm(从上到下)
   (1)基本思想:不断的删除网络中边介数最大的边，直到网络中每个节点都是一个社团为止
   
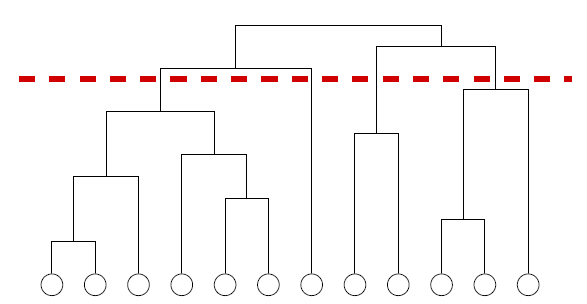
   (2)Drawback: at least O(𝑚𝑛) complexity(缺点:至少O(mn)复杂度)
2. FN algorithm(从下到上)
   (1)基本思想:不断的合并网络中距离最小的两个节点，直到网络中每个节点都是一个社团为止

Random Walk

1. 基本思想:在图中每个节点放一个walk，以概率1-α游走到该节点的邻居节点，以概率α随机跳跃到图中的任何一个节点，我们称α为跳转发生概率。用上一次游走的概率分布作为下一次游走的输入并反复迭代，这个概率分布会趋于收敛。即可得到一个稳定的概率分布。
   
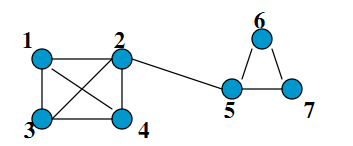
   在第一次游走的过程中, 一个游走者在节点1有33%的概率移动到节点2,3,4，而只有0%的概率选择5,6,7

2.重叠聚类算法

基于密集子图渗流(具体干了啥还没搞明白)

1. 最开始文章中认为community是由多个相互连通的k-clique构成,而并不是严格意义的clique的联系密集的区域(weak clique)也可以有相似作用;

基于动态标签传播

1. 标签传播算法思想——LPA
   
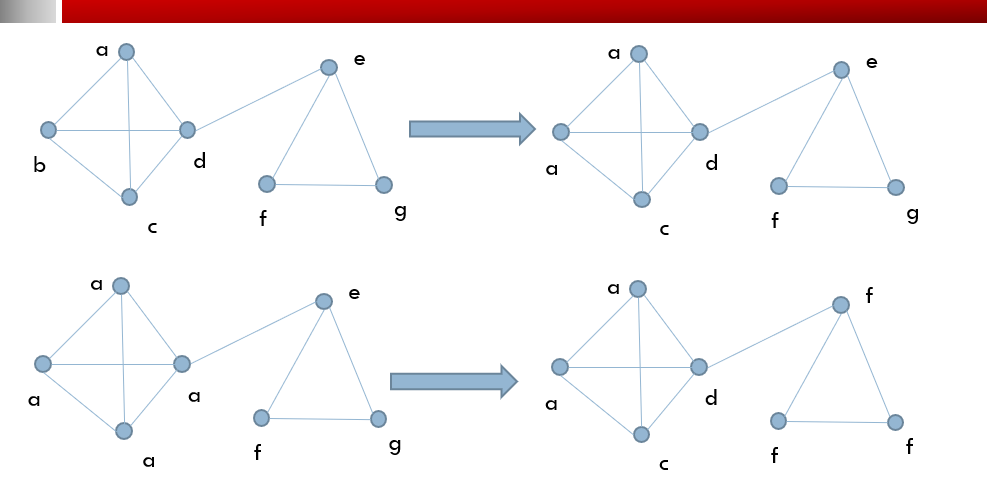
2. 检测重叠社团的标签传播——COPAR
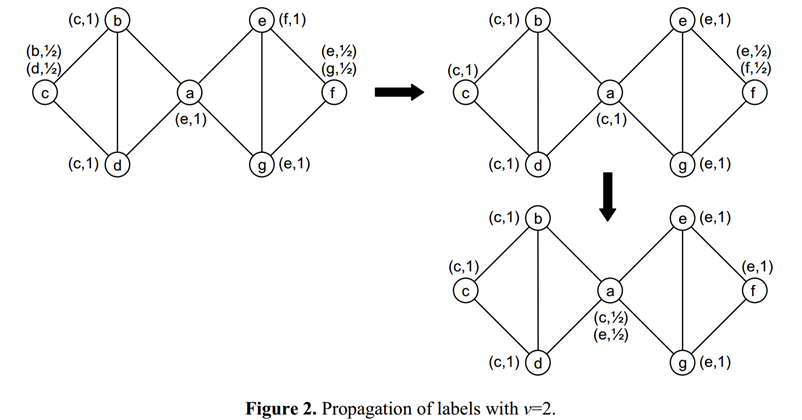
   啊啊啊,看不懂啊,赋两个图叭
   
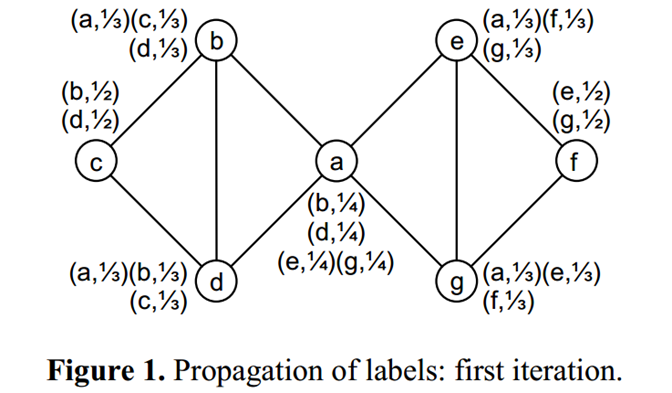
3. 检测重叠社团的标签传播——COPRA
   

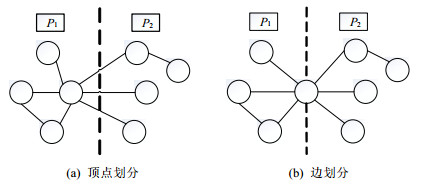
边划分

图划分定义: 给定一个图G=(V, E), V是图的顶点集合, E是图的边集合, 对于任意子集Es⊆E, V[Es]表示在Es中所有顶点的集合. 同样地, 对于任意子集Vs⊆V, E[Vs]表示两个端点都在Vs中的边的集合. 用N(v)表示顶点v的邻居顶点的集合. 图G被划分成k个分区, 其中, k是一个远小于|V|和|E|的正整数.

......没看懂边划分的公式

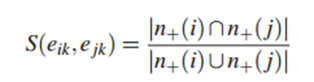
局部扩充思想——LFM、FOCS

1. 一篇挺详细的文章: https://blog.csdn.net/qq_16543881/article/details/122988044
2. LFM 算法是基于局部扩展优化类方法中的典型算法。该方法基于适应度函数局部最优化的思想对网络进行社区重叠划分。LFM 从一个任意种子节点开始扩展形成一个社区，当社区适应度值不再增加时停止扩展，然后再随机的从另一个未被划分的节点开始扩展以构建新的社区结构，当所有节点都被划分后算法终止。该算法可以通过调整参数 a 的大小发现社区层次性结构。
3. 分析公式:
   (1)适用度公式:
   
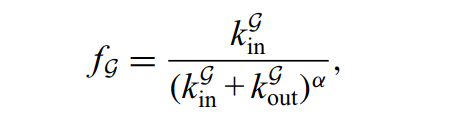
   其中k_in,k_out分别代表社区总的的内部度与外部度。社区的内部度等于社区内部链接数的两倍，外部度是社区的每个成员与图的其余部分的链接数。
   α是一个正实值参数，控制着社区的大小，决定了该方法的分辨率。调整α决定了观察社区的尺度。大的α值产生非常小的社区，小的α值反而提供大的社区。如果α足够小，所有的节点最终都在同一个集群中，即网络本身。我们发现，在大多数情况下，对于α < 0.5,只有一个群落;对于α > 2,恢复到最小的社区。自然的选择是α = 1,因为它是内部度与社区总度的比值。
   (2)节点对于社区的适应度:
   
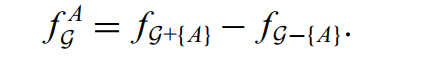
   定义为社区G的适应度在有节点a和无节点a时的变化量.

3.基于目标函数优化(没大看明白....)

Algorithm_community detection

Modularity(模块度)

1. 一篇超详细的文章: https://qinyuenlp.com/article/fba09bc9bda7/
2. 原始定义:
   
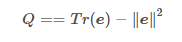
   其中迹(Tr(e)): 对于一个给定的网络G=(V,E),其中V为网络的节点集,E为网络的边集。将G划分为q个社区,我们用一个qxq的对称矩阵e来表示该划分,e中的每个元素表示连接社区i与社区j的边在G的全部边中所占的比例显然有∑_i,je_ij=1。矩阵e的迹Tr(e)表示连接社区内部节点的边的占比，一个好的社区划分应该有一个数值很高的迹。
3. 考虑节点度的模块度
   
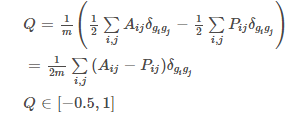
   m表示网络的总边数.
   12∑_i,jA_ijδ_gigj表示网络的社团内部边的数量.
   12∑_i,jP_ijδ_gigj表示社区内部边数的期望值.
   其中δ_ij是一个克罗内克函数(Kronecker delta):
   

Resolution limit in community detection