MCSDK 扇区判断解析
前言
本文为学习st的电机库MCSDK笔记，记录判断扇区的逻辑，并结合其他文章进行对比。
关键词：SVPWM，MCSDK,FOC
扇区判断
参考文章：《彻底吃透SVPWM如此简单》
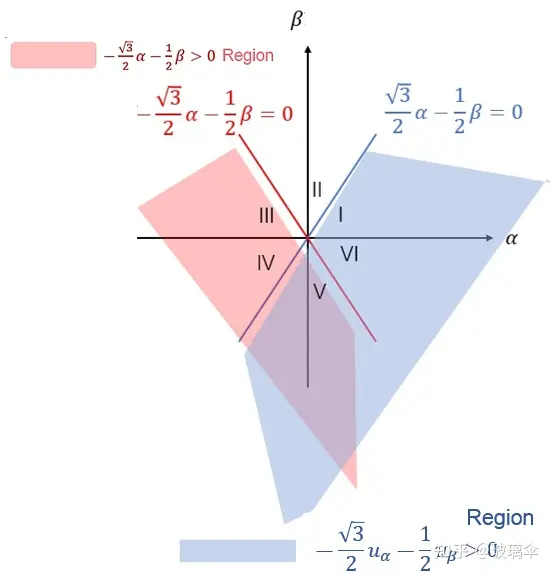
参考图1，为了便于判断扇区，将αβ坐标系用三条直线分割，分别是：
通过判断向量在每条直线的上下即可判断扇区。
因此记
对XYZ的大小进行判断，即可得知当前所在扇区
(注：这里除2的原因目前不太清楚；st的αβ坐标系以向下为正)。
| 扇区 | X | Y | Z |
|---|---|---|---|
| 1 | \(>0\) | \(>0\) | \(<0\) |
| 2 | \(>0\) | \(>0\) | \(>0\) |
| 3 | \(>0\) | \(<0\) | \(>0\) |
| 4 | \(<0\) | \(<0\) | \(>0\) |
| 5 | \(<0\) | \(<0\) | \(<0\) |
| 6 | \(<0\) | \(>0\) | \(<0\) |
对比ST代码：
wUAlpha = Valfa_beta.alpha * (int32_t)pHandle->hT_Sqrt3;
wUBeta = -(Valfa_beta.beta * ((int32_t)pHandle->PWMperiod)) * 2;
wX = wUBeta;
wY = (wUBeta + wUAlpha) / 2;
wZ = (wUBeta - wUAlpha) / 2;
/* Sector calculation from wX, wY, wZ */
if (wY < 0){
if (wZ < 0){}
else /* wZ >= 0 */
if (wX <= 0){}
else /* wX > 0 */
{}
}
else /* wY > 0 */
{
if (wZ >= 0)
{}
else /* wZ < 0 */
if ( wX <= 0 ){}
else /* wX > 0 */
{}
}
首先，根据传入的αβ值生成中间值wUAlpha,wUBeta。有
计算得
根据\(wX,wY,wZ\)目前可以确定扇区，但是还无法确定各向量的作用时间。
时间计算
先分析st的计算流程：
if (wY < 0){
if (wZ < 0)
{
pHandle->Sector = SECTOR_5;
wTimePhA = (((int32_t)pHandle->PWMperiod) / 4) + ((wY - wZ) / (int32_t)262144);
wTimePhB = wTimePhA + (wZ / 131072);
wTimePhC = wTimePhA - (wY / 131072) ;
}
}
wY<0时，wZ<0时，扇区为5。
然后看\(T_a,T_b,T_c\)的计算，和\(wY,wZ\)有关，且随扇区变化。
看结果看不出来，需要正向推导下。
参考图2：
记总导通时间为\(T_s\)有
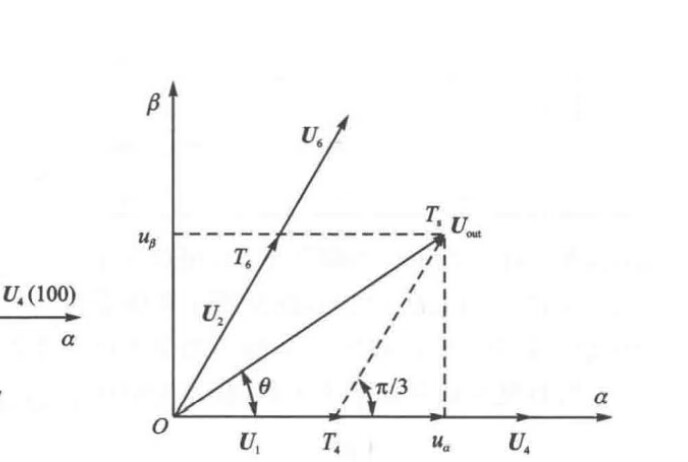
将\(U_{out}\)分解，记\(T_4\)为基本矢量\(V_4\)的作用时间，\(T_6\)为基本矢量\(V_6\)的作用时间，有
将\(U_{out}\)在αβ轴的投影记为\(U_{\alpha},-U_{\beta}\)，有
联立\((1)\)~\((6)\)可得：
解得
在一般情况下，\(|U_4| = |U_6| = \frac{2U_{dc}}{3}\),其中\(|U_{dc}|\)为最大输出相电压，但是\(|U_{out}|\)无法完全维持在\(U_{dc}\),如图3所示：
为了避免输出电压失真，将\(|U_{max}|\)限制在\(|\frac{\sqrt{3}U_x}{2}|\)
则有:
在ST的库中，\(\frac{U_{\alpha}}{|Umax|} = V_{\alpha},\frac{U_{\beta}}{|Umax|} = V_{\beta}\),因此
在第一扇区，矢量分布如图4：
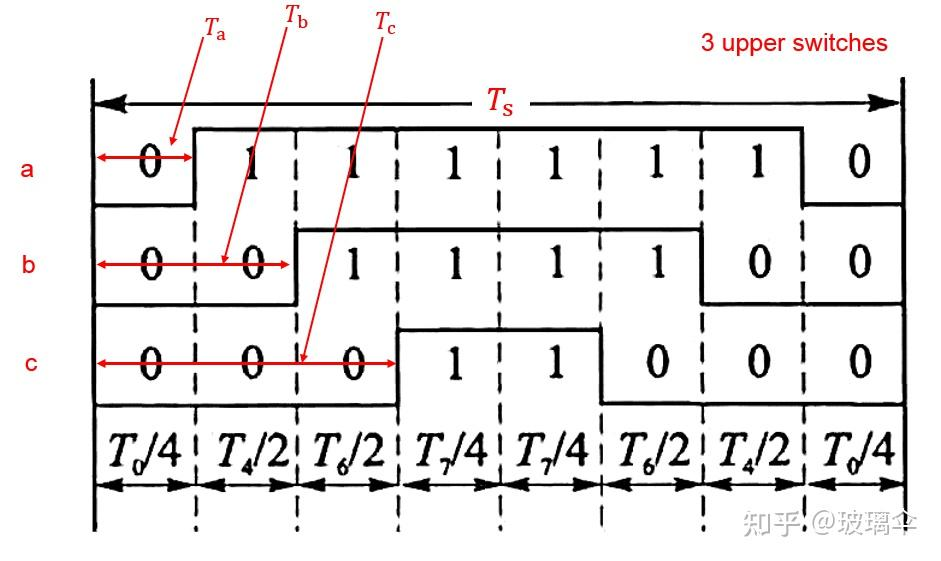
由于采用中心对称计数模式，计算单侧时间即可。
可得
代码解读
这时候对比st的代码
pHandle->Sector = SECTOR_1;
wTimePhA = (((int32_t)pHandle->PWMperiod) / 4)+ ((wX - wZ) / (int32_t)262144);
wTimePhB = wTimePhA + (wZ / 131072);
wTimePhC = wTimePhB - (wX / 131072);
显然
观察\(wX\):
其中\(V_β\)为int16_t，即q15格式。在前面有
显然\(V_β\in [-1,1]\),为浮点型。因此这里除以\(32768\)实际上是将q15转换为float。
因此st计算公式可表示为
可以看到，和我们推算出的公式符号不一致。
参考st的定时器配置，发现st采用的向下中心计数模式，前面参考的图为向上计数，因此重新推算公式如下：
和代码中吻合。
其他扇区按照相同方法推算，得出每个扇区对应的计算公式，实际使用时，根据扇区选择对应的计算公式即可。
过调制
前面为了矢量不失真，将\(|U_{max}|\)限制了在\(|\frac{\sqrt{3}}{2}U_x|\)即\(|\frac{\sqrt{3}}{3}U_{dc}|\)
将\([0,\frac{\sqrt{3}U_{dc}}{3}]\)称之为线性区，在线性区内，\(U_{out}和U_{\alpha}U_{\beta}\)线性相关；
将\((\frac{\sqrt{3}}{3}U_{dc},\frac{2}{3}U_{dc}]\)称之为过调制区，在过调制区内，需要对\(U_{\alpha}U_{\beta}\)进行缩放，以保证合成矢量\(U_{out}\)不超出最大幅值。过调制方法这里不再探讨，可以参考相关文章：
《STM32 MC SDK Overmodulation (new in V5.Y) - stm32mcu (stmicroelectronics.cn)》
