数据竞赛总结
1.数据竞赛流程

数据分析主要目的是分析数据原有的分布和内容;
特征工程目的是从数据中抽取出有效的特征;
模型训练与验证部分包括数据划分的方法以及数据训练的方法;
模型融合参考我的另一篇介绍模型融合的博客。
1.1.数据分析
在拿到数据之后,首先要做的就是要数据分析(Exploratory Data Analysis,EDA)。数据分析是数 据挖掘中重要的步骤,同时也在其他阶段反复进行。可以说数据分析是数据挖掘中至关重要的一步,它给之后的步骤提供了改进的方向,也是直接可以理解数据的方式。拿到数据之后,我们必须要明确以下几件事情:
(1)数据是如何产生的,数据又是如何存储的;
(2)数据是原始数据,还是经过人工处理(二次加工的);
(3)数据由那些业务背景组成的,数据字段又有什么含义;
(4)数据字段是什么类型的,每个字段的分布是怎样的;
(5)训练集和测试集的数据分布是否有差异;
(6)在分析数据的过程中,还必须要弄清楚的以下数据相关的问题:
(7)数据量是否充分,是否有外部数据可以进行补充;
(8)数据本身是否有噪音,是否需要进行数据清洗和降维操作;
(9)赛题的评价函数是什么,和数据字段有什么关系;
(10)数据字段与赛题标签的关系;
1.2数据预处理
数据预处理的主要步骤分为:(1)数据清理;(2)数据集成;(3)数据规约;(4)数据变换。
(1)数据清理(data cleaning) 的主要思想是通过填补缺失值、光滑噪声数据,平滑或删除离群点,并解决数据的不一致性来“清理“数据。
(1.1)缺失值的处理
由于现实世界中,获取信息和数据的过程中,会存在各类的原因导致数据丢失和空缺。针对这些缺失值的处理方法,主要是基于变量的分布特性和变量的重要性(信息量和预测能力)采用不同的方法。主要分为以下几种:
-
删除变量:若变量的缺失率较高(大于80%),覆盖率较低,且重要性较低,可以直接将变量删除。
-
定值填充:工程中常见用-9999进行替代
-
统计量填充:若缺失率较低(小于95%)且重要性较低,则根据数据分布的情况进行填充。对于数据符合均匀分布,用该变量的均值填补缺失,对于数据存在倾斜分布的情况,采用中位数进行填补。
-
插值法填充:包括随机插值,多重差补法,热平台插补,拉格朗日插值,牛顿插值等
-
模型填充:使用回归、贝叶斯、随机森林、决策树等模型对缺失数据进行预测。
-
哑变量填充:若变量是离散型,且不同值较少,可转换成哑变量,例如性别SEX变量,存在male,fameal,NA三个不同的值,可将该列转换成 IS_SEX_MALE, IS_SEX_FEMALE, IS_SEX_NA。若某个变量存在十几个不同的值,可根据每个值的频数,将频数较小的值归为一类'other',降低维度。此做法可最大化保留变量的信息。
总结来看,楼主常用的做法是:先用pandas.isnull.sum()检测出变量的缺失比例,考虑删除或者填充,若需要填充的变量是连续型,一般采用均值法和随机差值进行填充,若变量是离散型,通常采用中位数或哑变量进行填充。
注意:若对变量进行分箱离散化,一般会将缺失值单独作为一个箱子(离散变量的一个值)
(1.2)离群点处理
异常值是数据分布的常态,处于特定分布区域或范围之外的数据通常被定义为异常或噪声。异常分为两种:“伪异常”,由于特定的业务运营动作产生,是正常反应业务的状态,而不是数据本身的异常;“真异常”,不是由于特定的业务运营动作产生,而是数据本身分布异常,即离群点。主要有以下检测离群点的方法:
-
简单统计分析:根据箱线图、各分位点判断是否存在异常,例如pandas的describe函数可以快速发现异常值。
-
3∂原则:若数据存在正态分布,偏离均值的3∂之外. 通常定义P(|x-u| > 3∂) <= 0.003范围内的点为离群点。
-
基于绝对离差中位数(MAD):这是一种稳健对抗离群数据的距离值方法,采用计算各观测值与平均值的距离总和的方法。放大了离群值的影响。
-
基于距离:通过定义对象之间的临近性度量,根据距离判断异常对象是否远离其他对象,缺点是计算复杂度较高,不适用于大数据集和存在不同密度区域的数据集
-
基于密度:离群点的局部密度显著低于大部分近邻点,适用于非均匀的数据集
-
基于聚类:利用聚类算法,丢弃远离其他簇的小簇。
总结来看,在数据处理阶段将离群点作为影响数据质量的异常点考虑,而不是作为通常所说的异常检测目标点,因而楼主一般采用较为简单直观的方法,结合箱线图和MAD的统计方法判断变量的离群点。
具体的处理手段:
-
根据异常点的数量和影响,考虑是否将该条记录删除,信息损失多
-
若对数据做了log-scale 对数变换后消除了异常值,则此方法生效,且不损失信息
-
平均值或中位数替代异常点,简单高效,信息的损失较少
-
在训练树模型时,树模型对离群点的鲁棒性较高,无信息损失,不影响模型训练效果
(1.3)噪声处理
噪声是变量的随机误差和方差,是观测点和真实点之间的误差。通常的处理办法:对数据进行分箱操作,等频或等宽分箱,然后用每个箱的平均数,中位数或者边界值(不同数据分布,处理方法不同)代替箱中所有的数,起到平滑数据的作用。另外一种做法是,建立该变量和预测变量的回归模型,根据回归系数和预测变量,反解出自变量的近似值。
(2)数据集成:将多个数据源中的数据结合成、存放在一个一致的数据存储,如数据仓库中。这些源可能包括多个数据库、数据方或一般文件。
(2.1)实体识别问题:例如,数据分析者或计算机如何才能确信一个数 据库中的 customer_id 和另一个数据库中的 cust_number 指的是同一实体?通常,数据库和数据仓库 有元数据——关于数据的数据。这种元数据可以帮助避免模式集成中的错误。
(2.2)冗余问题。一个属性是冗余的,如果它能由另一个表“导出”;如年薪。属性或 维命名的不一致也可能导致数据集中的冗余。用相关性检测冗余:数值型变量可计算相关系数矩阵,标称型变量可计算卡方检验。
(2.3)数据值的冲突和处理:不同数据源,在统一合并时,保持规范化,去重。
(3)数据规约:用来得到数据集的归约表示,它小得多,但仍接近地保持原数据的完整性。这样,在归约后的数据集上挖掘将更有效,并产生相同(或几乎相同)的分析结果。一般有如下策略:
(3.1)维度规约
用于数据分析的数据可能包含数以百计的属性,其中大部分属性与挖掘任务不相关,是冗余的。维度归约通过删除不相关的属性,来减少数据量,并保证信息的损失最小。
(3.2)属性子集选择:目标是找出最小属性集,使得数据类的概率分布尽可能地接近使用所有属性的原分布。在压缩 的属性集上挖掘还有其它的优点。它减少了出现在发现模式上的属性的数目,使得模式更易于理解。
-
逐步向前选择:该过程由空属性集开始,选择原属性集中最好的属性,并将它添加到该集合
中。在其后的每一次迭代,将原属性集剩下的属性中的最好的属性添加到该集合中。 -
逐步向后删除:该过程由整个属性集开始。在每一步,删除掉尚在属性集中的最坏属性。
-
向前选择和向后删除的结合:向前选择和向后删除方法可以结合在一起,每一步选择一个最 好的属性,并在剩余属性中删除一个最坏的属性。
python scikit-learn 中的递归特征消除算法Recursive feature elimination (RFE),就是利用这样的思想进行特征子集筛选的,一般考虑建立SVM或回归模型。
单变量重要性:分析单变量和目标变量的相关性,删除预测能力较低的变量。这种方法不同于属性子集选择,通常从统计学和信息的角度去分析。
-
pearson相关系数和卡方检验,分析目标变量和单变量的相关性。
-
回归系数:训练线性回归或逻辑回归,提取每个变量的表决系数,进行重要性排序。
-
树模型的Gini指数:训练决策树模型,提取每个变量的重要度,即Gini指数进行排序。
-
Lasso正则化:训练回归模型时,加入L1正则化参数,将特征向量稀疏化。
-
IV指标:风控模型中,通常求解每个变量的IV值,来定义变量的重要度,一般将阀值设定在0.02以上。
以上提到的方法,没有讲解具体的理论知识和实现方法,需要同学们自己去熟悉掌握。楼主通常的做法是根据业务需求来定,如果基于业务的用户或商品特征,需要较多的解释性,考虑采用统计上的一些方法,如变量的分布曲线,直方图等,再计算相关性指标,最后去考虑一些模型方法。如果建模需要,则通常采用模型方法去筛选特征,如果用一些更为复杂的GBDT,DNN等模型,建议不做特征选择,而做特征交叉。
(3.2)维度变换
维度变换是将现有数据降低到更小的维度,尽量保证数据信息的完整性。楼主将介绍常用的几种有损失的维度变换方法,将大大地提高实践中建模的效率
-
主成分分析(PCA)和因子分析(FA):PCA通过空间映射的方式,将当前维度映射到更低的维度,使得每个变量在新空间的方差最大。FA则是找到当前特征向量的公因子(维度更小),用公因子的线性组合来描述当前的特征向量。
-
奇异值分解(SVD):SVD的降维可解释性较低,且计算量比PCA大,一般用在稀疏矩阵上降维,例如图片压缩,推荐系统。
-
聚类:将某一类具有相似性的特征聚到单个变量,从而大大降低维度。
-
线性组合:将多个变量做线性回归,根据每个变量的表决系数,赋予变量权重,可将该类变量根据权重组合成一个变量。
(4)数据变换:包括对数据进行规范化,离散化,稀疏化处理,达到适用于挖掘的目的。
(4.1)规范化处理
数据中不同特征的量纲可能不一致,数值间的差别可能很大,不进行处理可能会影响到数据分析的结果(会导致目标函数变“扁”。这样在进行梯度下降的时候,梯度的方向就会偏离最小值的方向,走很多弯路,即训练时间过长),因此,需要对数据按照一定比例进行缩放,使之落在一个特定的区域,便于进行综合分析。特别是基于距离的挖掘方法,聚类,KNN,SVM一定要做规范化处理。
-
(a)最大最小标准化(Min-Max Normalization):比较适用在数值比较集中的情况;
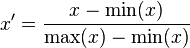
(b)Z-score标准化方法:要求原始数据的分布可以近似为高斯分布,否则归一化的效果会变得很糟糕。数据处理后符合标准正态分布,即均值为0,标准差为1
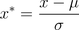
(c)非线性归一化:经常用在数据分化比较大的场景,有些数值很大,有些很小。该方法包括 log,正切等,需要根据数据分布的情况,决定非线性函数的曲线
(4.2)离散化处理
数据离散化是指将连续的数据进行分段,使其变为一段段离散化的区间。分段的原则有基于等距离、等频率或优化的方法。数据离散化的原因主要有以下几点:
-
模型需要:比如决策树、朴素贝叶斯等算法,都是基于离散型的数据展开的。如果要使用该类算法,必须将离散型的数据进行。有效的离散化能减小算法的时间和空间开销,提高系统对样本的分类聚类能力和抗噪声能力。
-
离散化的特征相对于连续型特征更易理解。
-
可以有效的克服数据中隐藏的缺陷,使模型结果更加稳定。
等频法:使得每个箱中的样本数量相等,例如总样本n=100,分成k=5个箱,则分箱原则是保证落入每个箱的样本量=20。
等宽法:使得属性的箱宽度相等,例如年龄变量(0-100之间),可分成 [0,20],[20,40],[40,60],[60,80],[80,100]五个等宽的箱。
聚类法:根据聚类出来的簇,每个簇中的数据为一个箱,簇的数量模型给定。
(4.3)稀疏化处理
针对离散型且标称变量,无法进行有序的LabelEncoder时,通常考虑将变量做0,1哑变量的稀疏化处理,例如动物类型变量中含有猫,狗,猪,羊四个不同值,将该变量转换成is_猪,is_猫,is_狗,is_羊四个哑变量。若是变量的不同值较多,则根据频数,将出现次数较少的值统一归为一类'rare'。稀疏化处理既有利于模型快速收敛,又能提升模型的抗噪能力。
1.2特征工程
特征工程本质做的工作是,将数据字段转换成适合模型学习的形式,降低模型的学习难度。可以从一下几个角度构建新的特征:
(1)数据中每个字段的含义、分布、缺失情况;
(2)数据中每个字段的与赛题标签的关系;
(3)数据字段两两之间,或者三者之间的关系;
2. 其他问题
2.1 样本不均衡问题
- 数据角度:欠采样/过采样/SMOTE算法等
- 模型角度:调整lr的阈值/采用树模型等
- 评估角度:采用F1值/ROC曲线等
2.2 无标签样本问题
- 半监督学习方法/聚类思考等
2.3 欠拟合/过拟合问题
- 欠拟合
- 特征扩充/非线性模型等
- 过拟合
- 扩充数据集/正则化/early stoppping/交叉验证
- Dropout/batch normalization
参考链接:
https://blog.csdn.net/Datawhale/article/details/100981726
https://blog.csdn.net/w47478/article/details/104874580/
https://www.cnblogs.com/zhengzhicong/p/12728491.html#_label0_2




