力扣杯--2020春季全国编程大赛
1. 拿硬币
桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。
示例 1:
输入:
[4,2,1]输出:
4解释:第一堆力扣币最少需要拿 2 次,第二堆最少需要拿 1 次,第三堆最少需要拿 1 次,总共 4 次即可拿完。
示例 2:
输入:
[2,3,10]输出:
8
限制:
1 <= n <= 41 <= coins[i] <= 10
class Solution:
def minCount(self, coins: List[int]) -> int:
return sum(ceil(c / 2) for c in coins)
2. 传递信息
小朋友 A 在和 ta 的小伙伴们玩传信息游戏,游戏规则如下:
- 有 n 名玩家,所有玩家编号分别为 0 ~ n-1,其中小朋友 A 的编号为 0
- 每个玩家都有固定的若干个可传信息的其他玩家(也可能没有)。传信息的关系是单向的(比如 A 可以向 B 传信息,但 B 不能向 A 传信息)。
- 每轮信息必须需要传递给另一个人,且信息可重复经过同一个人
给定总玩家数 n,以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数;若不能到达,返回 0。
示例 1:
输入:
n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3输出:
3解释:信息从小 A 编号 0 处开始,经 3 轮传递,到达编号 4。共有 3 种方案,分别是 0->2->0->4, 0->2->1->4, 0->2->3->4。
示例 2:
输入:
n = 3, relation = [[0,2],[2,1]], k = 2输出:
0解释:信息不能从小 A 处经过 2 轮传递到编号 2
限制:
2 <= n <= 101 <= k <= 51 <= relation.length <= 90, 且 relation[i].length == 20 <= relation[i][0],relation[i][1] < n 且 relation[i][0] != relation[i][1]
class Solution:
def numWays(self, n: int, relation: List[List[int]], k: int) -> int:
L = [[] for _ in range(n + 1)]
for a, b in relation:
L[a].append(b)
D = defaultdict(int)
D[0] = 1
for _ in range(k):
nD = defaultdict(int)
for d in D:
for c in L[d]:
nD[c] += D[d]
D = nD
return D[n - 1]
#递归解决
from collections import defaultdict
class Solution:
def numWays(self, n: int, relation: List[List[int]], k: int) -> int:
dct = defaultdict(list)
for i,j in relation:
dct[i].append(j)
res = 0
def dfs(cur, level):
nonlocal res
if level == k:
if cur == n-1:
res += 1
return
for next_val in dct[cur]:
dfs(next_val, level+1)
dfs(0, 0)
return res
3. 剧情触发时间
在战略游戏中,玩家往往需要发展自己的势力来触发各种新的剧情。一个势力的主要属性有三种,分别是文明等级(C),资源储备(R)以及人口数量(H)。在游戏开始时(第 0 天),三种属性的值均为 0。随着游戏进程的进行,每一天玩家的三种属性都会对应增加,我们用一个二维数组 increase 来表示每天的增加情况。这个二维数组的每个元素是一个长度为 3 的一维数组,例如 [[1,2,1],[3,4,2]] 表示第一天三种属性分别增加 1,2,1 而第二天分别增加 3,4,2。所有剧情的触发条件也用一个二维数组 requirements 表示。这个二维数组的每个元素是一个长度为 3 的一维数组,对于某个剧情的触发条件 c[i], r[i], h[i],如果当前 C >= c[i] 且 R >= r[i] 且 H >= h[i] ,则剧情会被触发。
根据所给信息,请计算每个剧情的触发时间,并以一个数组返回。如果某个剧情不会被触发,则该剧情对应的触发时间为 -1 。
示例 1:
输入:
increase = [[2,8,4],[2,5,0],[10,9,8]]requirements = [[2,11,3],[15,10,7],[9,17,12],[8,1,14]]输出:
[2,-1,3,-1]解释:
初始时,C = 0,R = 0,H = 0
第 1 天,C = 2,R = 8,H = 4
第 2 天,C = 4,R = 13,H = 4,此时触发剧情 0
第 3 天,C = 14,R = 22,H = 12,此时触发剧情 2
剧情 1 和 3 无法触发。
示例 2:
输入:
increase = [[0,4,5],[4,8,8],[8,6,1],[10,10,0]]requirements = [[12,11,16],[20,2,6],[9,2,6],[10,18,3],[8,14,9]]输出:
[-1,4,3,3,3]
示例 3:
输入:
increase = [[1,1,1]]requirements = [[0,0,0]]输出:
[0]
限制:
1 <= increase.length <= 100001 <= requirements.length <= 1000000 <= increase[i] <= 100 <= requirements[i] <= 100000
class Solution:
def getTriggerTime(self, increase: List[List[int]], requirements: List[List[int]]) -> List[int]:
C, R, H = [0], [0], [0]
for c, r, h in increase:
C.append(C[-1] + c)
R.append(R[-1] + r)
H.append(H[-1] + h)
n = len(increase)
D = []
for c, r, h in requirements:
c = bisect_left(C, c)
r = bisect_left(R, r)
h = bisect_left(H, h)
m = max(c, r, h)
D.append(-1 if m == n + 1 else m)
return D
小知识:python的bisect模块一般用在二分查找中,,几个函数说明如下:
(1)bisect_left(L,x): 在L中查找x,x存在时返回x左侧的位置,x不存在返回应该插入的位置;
(2)bisect_right(L,x):在L中查找x,x存在时返回x右侧的位置,x不存在返回应该插入的位置;
(3)insort_left(L,x) : 将x插入到列表L中,x存在时插入在x左侧;
(3)insort_right(L,x) : 将x插入到列表L中,x存在时插入在x右侧;
4. 最小跳跃次数
为了给刷题的同学一些奖励,力扣团队引入了一个弹簧游戏机。游戏机由 N 个特殊弹簧排成一排,编号为 0 到 N-1。初始有一个小球在编号 0 的弹簧处。若小球在编号为 i 的弹簧处,通过按动弹簧,可以选择把小球向右弹射 jump[i] 的距离,或者向左弹射到任意左侧弹簧的位置。也就是说,在编号为 i 弹簧处按动弹簧,小球可以弹向 0 到 i-1 中任意弹簧或者 i+jump[i] 的弹簧(若 i+jump[i]>=N ,则表示小球弹出了机器)。小球位于编号 0 处的弹簧时不能再向左弹。
为了获得奖励,你需要将小球弹出机器。请求出最少需要按动多少次弹簧,可以将小球从编号 0 弹簧弹出整个机器,即向右越过编号 N-1 的弹簧。
示例 1:
输入:
jump = [2, 5, 1, 1, 1, 1]输出:
3解释:小 Z 最少需要按动 3 次弹簧,小球依次到达的顺序为 0 -> 2 -> 1 -> 6,最终小球弹出了机器。
限制:
1 <= jump.length <= 10^61 <= jump[i] <= 10000
class Solution:
def minJump(self, jump: List[int]) -> int:
size = len(jump)
visited = set([0])
res = 0
def bfs(roots,depth):
nonlocal res, visited
tmp = set()
for root in roots:
max_dist = root + jump[root]
if max_dist >= size:
res = depth
return
tmp.add(max_dist)
fur = max(list(roots))
for e in (set(range(fur))-visited): tmp.add(e)
# visited ^= tmp
for e in tmp: visited.add(e)
bfs(tmp,depth+1)
bfs([0],1)
return res
5. 二叉树任务调度
任务调度优化是计算机性能优化的关键任务之一。在任务众多时,不同的调度策略可能会得到不同的总体执行时间,因此寻求一个最优的调度方案是非常有必要的。
通常任务之间是存在依赖关系的,即对于某个任务,你需要先完成他的前导任务(如果非空),才能开始执行该任务。我们保证任务的依赖关系是一棵二叉树,其中 root 为根任务,root.left 和 root.right 为他的两个前导任务(可能为空),root.val 为其自身的执行时间。
在一个 CPU 核执行某个任务时,我们可以在任何时刻暂停当前任务的执行,并保留当前执行进度。在下次继续执行该任务时,会从之前停留的进度开始继续执行。暂停的时间可以不是整数。
现在,系统有两个 CPU 核,即我们可以同时执行两个任务,但是同一个任务不能同时在两个核上执行。给定这颗任务树,请求出所有任务执行完毕的最小时间。
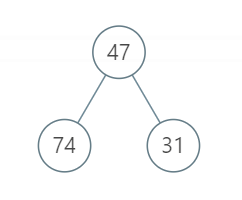
示例 1:
输入:root = [47, 74, 31]
输出:121
解释:根节点的左右节点可以并行执行31分钟,剩下的43+47分钟只能串行执行,因此总体执行时间是121分钟。
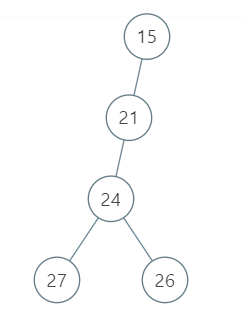
示例 2:
输入:root = [15, 21, null, 24, null, 27, 26]
输出:87
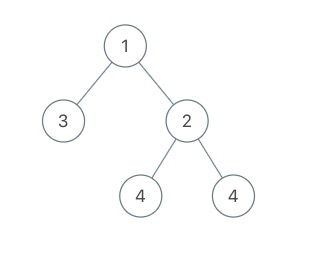
示例 3:
输入:root = [1,3,2,null,null,4,4]
输出:7.5
限制:
1 <= 节点数量 <= 10001 <= 单节点执行时间 <= 1000
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def minimalExecTime(self, root: TreeNode) -> float:
def L(r):
if not r:
return (0, 0)
ls, ld = L(r.left)
rs, rd = L(r.right)
if ls > rs:
ls, ld, rs, rd = rs, rd, ls, ld
s, d = r.val, ld + rd + ls * 2
c = max(0, rs - ls - ld)
s += c
d += rs - ls - c
return (s, d)
s, d = L(root)
return s + d / 2