LSTM改善RNN梯度弥散和梯度爆炸问题

我们给定一个三个时间的RNN单元，如下：

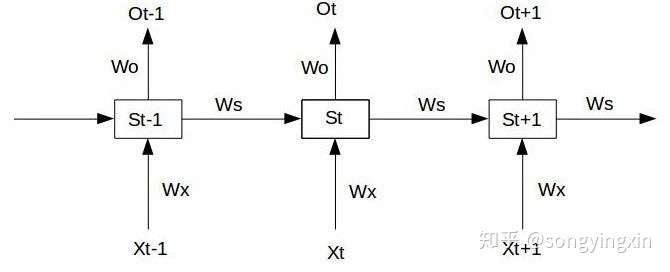
我们假设最左端的输入 S_0 为给定值， 且神经元中没有激活函数（便于分析）， 则前向过程如下：

S_1 = W_xX_1 + W_sS_0 + b_1 \qquad \qquad \qquad O_1 = W_oS_1 + b_2 \\ S_2 = W_xX_2 + W_sS_1 + b_1 \qquad \qquad \qquad O_2 = W_oS_2 + b_2 \\ S_3 = W_xX_3 + W_sS_2 + b_1 \qquad \qquad \qquad O_3 = W_oS_3 + b_2 \\

在 t=3 时刻， 损失函数为 L_3 = \frac{1}{2}(Y_3 - O_3)^2 ，那么如果我们要训练RNN时， 实际上就是是对 W_x, W_s, W_o,b_1,b_2 求偏导， 并不断调整它们以使得 L_3 尽可能达到最小（参见反向传播算法与梯度下降算法)。

那么我们得到以下公式：

\frac{\delta L_3}{\delta W_0} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta W_0} \\ \frac{\delta L_3}{\delta W_x} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta W_x} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta W_x} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta S_1}\frac{\delta S_1}{\delta W_x} \\ \frac{\delta L_3}{\delta W_s} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta W_s} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta W_s} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta S_1}\frac{\delta S_1}{\delta W_s} \\

将上述偏导公式与第三节中的公式比较，我们发现， 随着神经网络层数的加深对 W_0 而言并没有什么影响， 而对 W_x, W_s 会随着时间序列的拉长而产生梯度消失和梯度爆炸问题。

根据上述分析整理一下公式可得， 对于任意时刻t对 W_x, W_s 求偏导的公式为：

\frac{\delta L_t}{\delta W_x } = \sum_{k=0}^t \frac{\delta L_t}{\delta O_t} \frac{\delta O_t}{\delta S_t}( \prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}} ) \frac{ \delta S_k }{\delta W_x} \\ \frac{\delta L_t}{\delta W_s } = \sum_{k=0}^t \frac{\delta L_t}{\delta O_t} \frac{\delta O_t}{\delta S_t}( \prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}} ) \frac{ \delta S_k }{\delta W_s}

由 以上可知，RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

参考：

https://www.cnblogs.com/bonelee/p/10475453.html

 

https://www.zhihu.com/question/34878706

posted @ 2019-07-09 19:13  USTC丶ZCC  阅读(1205)  评论(2)  编辑  收藏  举报