主席树
1 引入
主席树,全称可持久化权值线段树(有时也会用来代指可持久化线段树,毕竟二者差别不大)。所谓可持久化,就是可以保留每一个历史版本,并且支持操作的不可变特性。对于线段树而言,可持久化意味着它可以保留多个历史版本的线段树,并且支持对历史版本的访问与修改。
那么下面来看主席树的基本思想。
2 基本思想
保存每一个历史版本的线段树本身是简单的,直接开一堆线段树就行,但是显然这样做空间会爆炸。
我们考虑当我们进行一次单点修改的时候,实际上只有原树上的一条链被修改了权值。换句话说,当我们新建一个版本的时候,只需要新建一条链的信息,剩下的采用原版本信息即可。这样我们每次新增的节点就达到了 \(O(\log n)\) 个,可以接受。
例如下图即为修改 \(1\) 时新建节点情况:
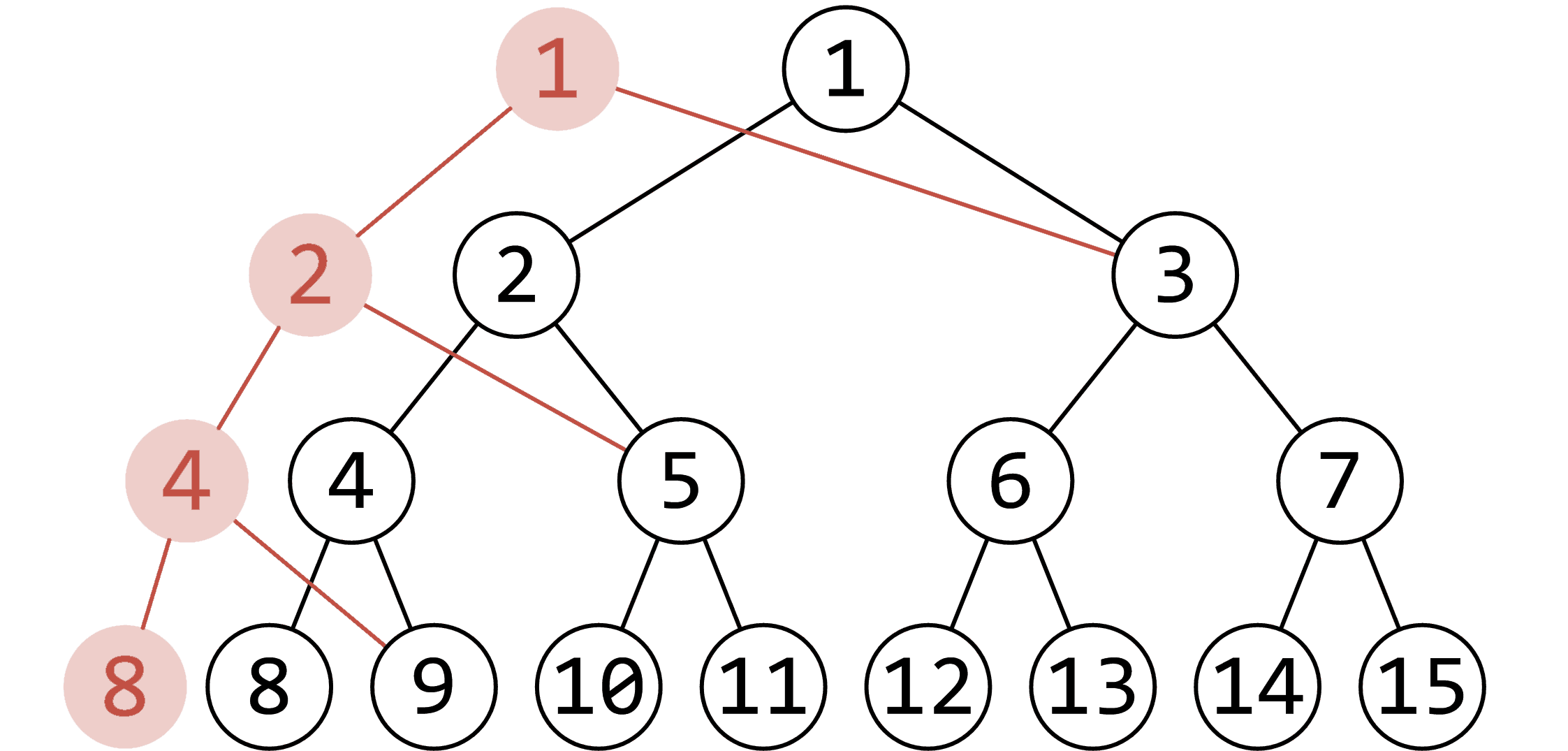
自然,由于每一次会复用原来的节点,所以左右儿子不能用朴素的 \(2\times p,2\times p+1\) 来存储,需要采用类似动态开点的方式存储。
上面我们讲的是单点修改的主席树,那么区间修改应该如何做呢?
考虑普通线段树怎样进行区间修改,不难想到就是下放标记、上传合并。但是由于主席树上有复用的节点,所以无法下放懒标记,也无法上传合并信息。这个时候我们想到了标记永久化,通过标记永久化我们就可以不用下放和上传操作,并且仍然只需要修改 \(O(\log n)\) 个节点的信息。如此便可在正确的时空复杂度内完成主席树的区间修改。
以上就是主席树的基本思想,下面来看几道例题。
3 例题
例 1: 【模板】可持久化线段树 2
题意: 求静态区间第 \(k\) 小。
先考虑对于全局求第 \(k\) 小怎么做,这个用权值线段树是显然的。先对原数组离散化,然后建一颗权值线段树。我们在线段树上遍历,如果左子树的数字总个数小于 \(k\),则说明目标在右子树内,遍历右子树即可;否则去遍历左子树。
现在如果要求区间 \([l,r]\) 的第 \(k\) 小值,实际上只需要知道 \([l,r]\) 这段区间内所有数字构成的权值线段树上的信息即可。考虑运用前缀和的思想,我们单次插入数组中的一个元素,建立一颗主席树,则主席树上每一个节点存储的就是 \([1,r]\) 内所有数字的信息。如果要求 \([l,r]\) 内的信息,用 \([1,r]\) 内的信息减去 \([1,l-1]\) 内的信息即可。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int Maxn = 2e5 + 5;
const int Inf = 2e9;
int n, m, a[Maxn], t[Maxn], tot;
int rt[Maxn];
namespace Sgt {
struct node {
int l, r, sum;
}t[Maxn << 5];
#define lp t[p].l
#define rp t[p].r
int tot = 0;
void build(int &p, int l, int r) {
p = ++tot;
t[p].sum = 0;
if(l == r) return ;
int mid = (l + r) >> 1;
build(lp, l, mid), build(rp, mid + 1, r);
}
int mdf(int p, int l, int r, int x) {//p 为上一版本树上节点
int rt = ++tot;//建新节点
t[rt] = t[p];
t[rt].sum++;
if(l == r) return rt;
int mid = (l + r) >> 1;
if(x <= mid) t[rt].l = mdf(lp, l, mid, x);
else t[rt].r = mdf(rp, mid + 1, r, x);
return rt;
}
int query(int p, int q, int l, int r, int k) {
if(l == r) return l;
int mid = (l + r) >> 1, res = t[t[q].l].sum - t[t[p].l].sum;//前缀和相减
if(res < k) return query(t[p].r, t[q].r, mid + 1, r, k - res);
else return query(t[p].l, t[q].l, l, mid, k);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> a[i];
t[++tot] = a[i];
}
sort(t + 1, t + tot + 1);
tot = unique(t + 1, t + tot + 1) - t - 1;
for(int i = 1; i <= n; i++) {
a[i] = lower_bound(t + 1, t + tot + 1, a[i]) - t;
}
Sgt::build(rt[0], 1, tot);
for(int i = 1; i <= n; i++) {
rt[i] = Sgt::mdf(rt[i - 1], 1, tot, a[i]);
}
while(m--) {
int l, r, k;
cin >> l >> r >> k;
int pos = Sgt::query(rt[l - 1], rt[r], 1, tot, k);
cout << t[pos] << '\n';
}
return 0;
}
例 2: [SDOI2013] 森林
题意: 维护一个森林,支持合并两个连通块、求两点间权值第 \(k\) 小。
看到维护第 \(k\) 小不难想到主席树,但是这是一个树上问题,那么自然的将序列前缀和转化为树上前缀和即可。因此在主席树上跑的时候,当前权值区间的信息应该是用 \(u\) 处的信息加上 \(v\) 处的信息,减去 \(\text{lca}\) 和 \(\text{lca}\) 的父亲处的信息。
现在的问题就是怎样合并连通块,由于强制在线,除了暴力合并我们似乎没有什么更好的方式。那么就考虑启发式合并,每一次将节点数量小的合并到大的上面,然后暴力重构小的连通块中每一个点在主席树上的信息即可。这样做的复杂度是 \(O(n\log ^2 n)\) 的,完全可以通过。
当然由于我们还需要在合并后求 \(\text{lca}\),所以树剖肯定不可行,只能使用倍增,在暴力重构的时候一起更新倍增数组即可。
例 3: [AH2017/HNOI2017] 影魔
首先考虑这个贡献的含义:假设区间 \((l,r)\) 的最大值是 \(c\),当 \(c<k_l\) 且 \(c<k_r\) 时产生 \(p_1\) 贡献;否则当 \(c<k_l\) 或 \(c<k_r\) 时产生 \(p_2\) 贡献。
那么这就说明要产生贡献肯定有一个端点是最大值,那么考虑枚举 \(c\) 所在位置 \(i\),并预处理出 \(i\) 左侧和右侧第一个大于 \(c\) 的数的位置,记作 \(L_i,R_i\)。此时根据上面所述的贡献,会发现贡献分为如下类型:
- 当 \(L_i\) 在 \([a,b]\) 中时,所有 \(x\in(i,\min(R_i,b + 1))\) 的 \(x\) 可以与 \(L_i\) 一起产生 \(p_2\) 贡献。
- 当 \(R_i\) 在 \([a,b]\) 中时,所有 \(x\in(\max(a-1,L_i),i)\) 的 \(x\) 可以与 \(R_i\) 一起产生 \(p_2\) 贡献。
- 当 \(L_i,R_i\) 均在 \([a,b]\) 中时,\(L_i,R_i\) 可以一起产生 \(p_1\) 贡献。
- 对于任意 \((i,i+1)\) 点对,它们可以一起产生 \(p_1\) 贡献。
我们以第一个举例说明如何维护。当我们遇到一个 \(L_i\) 时,将 \((i,R_i)\) 这个区间中的数全部 \(+p_2\) 的贡献,然后对于一组询问 \([a,b]\),我们直接查询 \([a,b]\) 中所有数的和即可满足 \(x\in(i,\min(R_i,b + 1))\) 这个要求。但是此时还没有满足 \(L_i\in[a,b]\) 这个要求,不难发现运用一次前缀和之后用在 \(b\) 处求得的答案减去在 \(a-1\) 处求得的答案即可满足该条件,所以利用主席树维护上述信息即可。剩余三个操作是同理的。
代码如下:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int Maxn = 2e5 + 5;
const int Maxm = 1.6e7 + 5;
const int Inf = 2e9;
int n, m, p1, p2;
int a[Maxn];
int pre[Maxn], nxt[Maxn], s[Maxn], top;
int rt[Maxn];
namespace Sgt {
struct node {
int l, r;
ll sum, tag;
}t[Maxm];
#define lp t[p].l
#define rp t[p].r
int tot = 0;
void build(int &p, int l, int r) {
p = ++tot;
if(l == r) return ;
int mid = (l + r) >> 1;
build(lp, l, mid), build(rp, mid + 1, r);
}
int mdf(int p, int l, int r, int pl, int pr, int v) {//区间修改
int rt = ++tot;
t[rt] = t[p];
t[rt].sum += 1ll * (min(pr, r) - max(pl, l) + 1) * v;//直接修改区间和
if(pl <= l && r <= pr) {
t[rt].tag += v;//打标记
return rt;
}
int mid = (l + r) >> 1;
if(pl <= mid) t[rt].l = mdf(lp, l, mid, pl, pr, v);
if(pr > mid) t[rt].r = mdf(rp, mid + 1, r, pl, pr, v);
return rt;
}
ll query(int p, int l, int r, int pl, int pr, ll tag/*当前增加的标记*/) {//区间查询
if(pl <= l && r <= pr) {
return t[p].sum + 1ll * (r - l + 1) * tag;//加上一路上走过来的标记
}
int mid = (l + r) >> 1;
ll res = 0;
if(pl <= mid) res += query(lp, l, mid, pl, pr, tag + t[p].tag);
if(pr > mid) res += query(rp, mid + 1, r, pl, pr, tag + t[p].tag);
return res;
}
}
struct node {
int l, r, v;
};
vector <node> V[Maxn];
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> p1 >> p2;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= n; i++) {
while(top && a[s[top]] <= a[i]) top--;
if(top) pre[i] = s[top];
else pre[i] = 0;
s[++top] = i;
}
top = 0;
for(int i = n; i >= 1; i--) {
while(top && a[s[top]] <= a[i]) top--;
if(top) nxt[i] = s[top];
else nxt[i] = n + 1;
s[++top] = i;
}
for(int i = 1; i <= n; i++) {
V[pre[i]].push_back((node){i + 1, nxt[i] - 1, p2});
V[nxt[i]].push_back((node){pre[i] + 1, i - 1, p2});
V[pre[i]].push_back((node){nxt[i], nxt[i], p1});
V[i].push_back((node){i + 1, i + 1, p1});
}
Sgt::build(rt[0], 0, n + 1);
for(int i = 1; i <= n; i++) {
bool flg = 0;
for(auto p : V[i]) {
if(!flg) {
rt[i] = Sgt::mdf(rt[i - 1], 0, n + 1, p.l, p.r, p.v);
flg = 1;
}
else {
rt[i] = Sgt::mdf(rt[i], 0, n + 1, p.l, p.r, p.v);
}
}
}
while(m--) {
int l, r;
cin >> l >> r;
cout << Sgt::query(rt[r], 0, n + 1, l, r, 0) - Sgt::query(rt[l - 1], 0, n + 1, l, r, 0) << '\n';
}
return 0;
}
例 4: [国家集训队] middle
题意: 求出 \(l\in [a,b],r\in [c,d]\) 的所有区间 \([l,r]\) 的中位数的最大值。强制在线。
考虑区间中位数的求法,在此题中最合适且最常见的套路就是二分答案。我们二分中位数 \(mid\),然后看怎样判断其与答案的大小关系。不难想到的是,此时如果 \(\ge mid\) 的数的数量不比 \(<mid\) 的数的数量少,那么 \(mid\) 应该是小于等于最后答案的,否则应该大于最后答案。
将上述条件转化如下:将当前数列中所有 \(\ge mid\) 的数改为 \(-1\),\(< mid\) 的数改为 \(1\),若当前区间的和 \(\le 0\),则说明 \(mid\) 小于等于最终答案。
回到原题,我们二分出 \(mid\) 之后,自然是希望 \(mid\) 比最终答案小,也就是说我们要尽可能找到一个合法区间 \([l,r]\),使它的权值和 \(\le 0\),也就是要让它的和尽可能小。考虑到最后选出的 \([l,r]\) 实际上是从区间 \([a,d]\) 中,删去一个 \([a,b]\) 的前缀与 \([c,d]\) 的后缀得到的,由于 \([a,d]\) 的权值和一定,所以只需要让 \([a,b]\) 的前缀、\([c,d]\) 的后缀分别最大即可。这个显然可以直接用线段树维护出来。
最后的问题就是怎样构建出每个数对应的 \(1,-1\) 序列,如果每一次都暴力建线段树肯定不行。考虑从大到小建树,这样每一次由 \(1\) 改为 \(-1\) 的位置总数只有 \(n\),所以每一次修改用主席树维护即可。
例 5: [FJOI2016] 神秘数
题意: 令一个可重数字集合 \(S\) 的神秘数为最小的不能被 \(S\) 的子集和表示的正整数。给定一个序列,求集合 \(\{a_i\mid i\in[l,r]\}\) 的神秘数。
首先需要发现一个性质。如果当前可重集可以表示出 \([1,lim]\) 的所有正整数,那么如果下一个加入的数字 \(a \le lim+1\),则可重集可表示的数字会扩展到 \([1,lim+a]\);否则该可重集的神秘数就是 \(lim+1\)。
证明如下:
当前可重集可以表示 \([1,lim]\) 的所有正整数,那么加入 \(a\) 后可以表示的正整数就应该是 \([1,lim]\cup [a,lim+a]\)。如果 \(a\le lim+1\),则上面的集合就是 \([1,lim+a]\);否则中间就会存在无法被表示的正整数,而这其中最小的就是 \(lim+1\)。
对于每一个询问,考虑暴力扩展当前的可重集。设当前可重集中包含了值域在 \([1,res]\) 中的所有数,它们可以表示所有在 \([1,lim]\) 中的正整数,那么下一次可以加入的数的范围应该是 \([res+1,lim+1]\)。设值域在这个区间中的所有数的和为 \(sum\),若 \(sum=0\),答案就是 \(lim+1\);否则当前可重集的值域范围会扩展至 \([1,lim+1]\),而它能表示的正整数范围则会扩大至 \([1,lim+sum]\)。
不难发现上面的过程中需要求解区间 \([l,r]\) 中值域在 \([res+1,lim+1]\) 的数的总和,这个就可以用主席树来实现了。最后的问题就是暴力扩展的时间复杂度,我们考虑 \(lim\) 的最大值是题目中给出的 \(10^9\),而每一次加上的 $sum $ 的最小值是 \(res+1\)。根据手玩可以发现,最后 \(sum\) 前的系数是一个类似斐波那契数列的东西,而斐波那契数列的数量级是 \(2^n\) 的,所以暴力扩展的复杂度是 \(O(\log \sum A_i)\),总复杂度 \(O(m\log n\log \sum A_i)\),可以通过。
例 6: Dynamic Rankings
题意: 求动态区间第 \(k\) 小。
在例 1 中我们讲过求解静态区间第 \(k\) 小的方式,那么对于动态区间第 \(k\) 小,首先想到的一个暴力做法就是,对于修改 \(a_x\leftarrow y\),直接暴力将 \([x,n]\) 的所有主席树上的信息修改一遍,然后查询的时候按照同样方式查询即可。不过这样的复杂度显然太劣。
考虑到上面问题中,我们复杂度较高的地方在于修改。这时我们会想到,主席树本质上维护的是前缀和信息,在上面的算法中我们相当于是暴力修改前缀和数组,然后利用前缀和数组求出一段区间的信息。所以问题的本质其实就是单点修改、区间查询。
此时就不难想到维护这个东西可以利用树状数组优化,具体的,我们将树状数组上每一个节点看作一颗权值线段树,修改的时候遍历树状数组并修改每个节点对应的线段树上的信息。查询的时候仍然在线段树上二分,但是这个时候作差的不再是两个节点,而是被拆成树状数组上的 \(O(\log n)\) 个节点一起作差,剩下的与普通查询无异。
此时修改操作的复杂度是遍历树状数组的 \(O(\log n)\) 与线段树上修改的 \(O(\log n)\),查询的复杂度是线段树二分的 \(O(\log n)\) 与跳节点到左儿子或右儿子的 \(O(\log n)\),总复杂度即为 \(O((n+m)\log^2 n)\),可以通过。
上述过程就是树套树的另一种形式:树状数组套权值线段树。事实上用线段树套平衡树也可以通过此题,但是复杂度是三个 \(\log\),并没有这个做法优秀。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int Maxn = 2e5 + 5;
const int Inf = 2e9;
int n, m, a[Maxn];
int rt[Maxn];
namespace Sgt {
struct node {
int l, r, sum;
}t[Maxn << 8];
#define lp t[p].l
#define rp t[p].r
int tot = 0;
void pushup(int p) {
t[p].sum = t[lp].sum + t[rp].sum;
}
void mdf(int &p, int l, int r, int x, int val) {
if(!p) p = ++tot;
if(l == r) {
t[p].sum += val;
return ;
}
int mid = (l + r) >> 1;
if(x <= mid) mdf(lp, l, mid, x, val);
else mdf(rp, mid + 1, r, x, val);
pushup(p);
}
int query(int p[], int q[], int n1, int n2, int l, int r, int k) {
if(l == r) return l;
int mid = (l + r) >> 1, res = 0;
for(int i = 1; i <= n2; i++) res += t[t[q[i]].l].sum;
for(int i = 1; i <= n1; i++) res -= t[t[p[i]].l].sum;
if(res < k) {
for(int i = 1; i <= n1; i++) p[i] = t[p[i]].r;
for(int i = 1; i <= n2; i++) q[i] = t[q[i]].r;
return query(p, q, n1, n2, mid + 1, r, k - res);
}
else {
for(int i = 1; i <= n1; i++) p[i] = t[p[i]].l;
for(int i = 1; i <= n2; i++) q[i] = t[q[i]].l;
return query(p, q, n1, n2, l, mid, k);
}
}
}
namespace BIT {
int lowbit(int x) {
return x & (-x);
}
void mdf(int x, int val) {
for(int i = x; i <= n; i += lowbit(i)) {
Sgt::mdf(rt[i], 0, 1e9, a[x], val);
}
}
int p[Maxn], q[Maxn], n1, n2;
int query(int l, int r, int k) {
n1 = n2 = 0;
for(int i = r; i; i -= lowbit(i)) {
q[++n2] = rt[i];
}
for(int i = l - 1; i; i -= lowbit(i)) {
p[++n1] = rt[i];
}
return Sgt::query(p, q, n1, n2, 0, 1e9, k);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> a[i], BIT::mdf(i, 1);
while(m--) {
char opt;
int x, y, k;
cin >> opt >> x;
switch(opt) {
case 'C': {
cin >> k;
BIT::mdf(x, -1);
a[x] = k;
BIT::mdf(x, 1);
break;
}
case 'Q': {
cin >> y >> k;
cout << BIT::query(x, y, k) << '\n';
break;
}
}
}
return 0;
}


