分块和莫队
1 分块
1.1 概念简述
分块被称为 “优雅的暴力”。
对于一个区间 \([1,n]\)，我们将其分成若干个块。在处理整块时直接维护整块信息，达到降低时间复杂度的目的。
对于常规分块，设块长为 \(m\)，则一般情况下 \(m\) 取 \(\sqrt{n}\) 时复杂度最优。
下面举几例来说明分块如何降低时间复杂度。
1.2 分块实例
1.2.1 「例 1」
Problem：
维护区间加法，单点查询。
Solution：
巨佬可以直接用树状数组、线段树，我们来考虑一下分块。
对于每一个块维护一个加法标记 \(add_i\)，对于整块直接修改 \(add_i\)。
对于区间两端的零碎块，我们直接暴力修改 \(a_i\) 的值。
复杂度 \(O(n\sqrt n)\)。
Code：
#include <bits/stdc++.h>
#define MAXN 100010
using namespace std;
typedef long long LL;
const int INF = 2e9;
int n, a[MAXN], sq, bel[MAXN], mark[MAXN], st[MAXN], en[MAXN];
int main() {
ios::sync_with_stdio(0);
cin >> n;
sq = sqrt(n);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= sq; i++) {
st[i] = n / sq * (i - 1) + 1;
en[i] = n / sq * i;
}
en[sq] = n;
for (int i = 1; i <= sq; i++) {
for (int j = st[i]; j <= en[i]; j++) {
bel[j] = i;
}
}
while (n--) {
int op, l, r, c;
cin >> op >> l >> r >> c;
if (op == 0) {
if (bel[l] == bel[r]) {
for (int i = l; i <= r; i++) {
a[i] += c;
}
} else {
for (int i = l; i <= en[bel[l]]; i++) {
a[i] += c;
}
for (int i = st[bel[r]]; i <= r; i++) {
a[i] += c;
}
for (int i = bel[l] + 1; i < bel[r]; i++) {
mark[i] += c;
}
}
} else {
cout << a[r] + mark[bel[r]] << endl;
}
}
return 0;
}
1.2.2 「例 2」
Problem：
维护区间开方，区间查询。
Solution：
开根号操作无法维护总和，但我们发现值域是 \([0,2^{31}-1]\)，类比 P4145，开根号操作总计不会超过十次，对于已经是 \(1\) 的数字，再开根号没有意义。
所以在处理整块的时候，如果这一块内所有数都为 \(1\)，则无需修改，直接跳过即可；剩下的零碎块直接暴力修改即可，这样保证了修改操作不超时。
Code：
#include <bits/stdc++.h>
#define MAXN 100010
using namespace std;
typedef long long LL;
const int INF = 2e9;
void read(int &p) {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - 48;
ch = getchar();
}
p = x * f;
}
void write(int p) {
if (p < 0) {
putchar('-');
p *= -1;
}
if (p > 9)
write(p / 10);
putchar(p % 10 + '0');
return ;
}
int n, a[MAXN], sq, st[MAXN], ed[MAXN], sum[MAXN], mark[MAXN], bel[MAXN];
struct block {
void build() {
sq = sqrt(n);
for (int i = 1; i <= sq; i++) {
st[i] = n / sq * (i - 1) + 1;
ed[i] = n / sq * i;
}
ed[sq] = n;
for (int i = 1; i <= sq; i++) {
for (int j = st[i]; j <= ed[i]; j++) {
bel[j] = i;
sum[i] += a[j];
}
}
}
void change(int l, int r) {
int L = bel[l], R = bel[r];
if (L == R) {
for (int i = l; i <= r; i++) {
sum[L] -= a[i];
a[i] = sqrt(a[i]);
sum[L] += a[i];
}
} else {
for (int i = l; i <= ed[L]; i++) {
sum[L] -= a[i];
a[i] = sqrt(a[i]);
sum[L] += a[i];
}
for (int i = st[R]; i <= r; i++) {
sum[R] -= a[i];
a[i] = sqrt(a[i]);
sum[R] += a[i];
}
for (int i = L + 1; i < R; i++) {
if (mark[i] == 1)
continue;
sum[i] = 0;
mark[i] = 1;
for (int j = st[i]; j <= ed[i]; j++) {
a[j] = sqrt(a[j]);
sum[i] += a[j];
if (a[j] > 1)
mark[i] = 0;
}
}
}
}
int query(int l, int r) {
int L = bel[l], R = bel[r], ans = 0;
if (L == R) {
for (int i = l; i <= r; i++)
ans += a[i];
} else {
for (int i = l; i <= ed[L]; i++)
ans += a[i];
for (int i = st[R]; i <= r; i++)
ans += a[i];
for (int i = L + 1; i < R; i++)
ans += sum[i];
}
return ans;
}
};
block B;
int main() {
ios::sync_with_stdio(0);
read(n);
for (int i = 1; i <= n; i++)
read(a[i]);
B.build();
while (n--) {
int op, l, r, c;
read(op), read(l), read(r), read(c);
if (op == 0)
B.change(l, r);
else
cout << B.query(l, r) << endl;
}
return 0;
}
2 莫队
2.1 普通莫队
2.1.1 基础思想
莫队是一种离线算法，用于处理区间询问问题。
对于莫队的使用要求是：可以在 \(O(1)\) 的时间复杂度内移动左端点或右端点一次。
而莫队的基本思想是：将所有询问区间按照顺序排序，接着暴力移动区间端点。利用分块思想，将左端点 \(l\) 分块；以 \(l\) 所属的块的编号为第一关键字，以 \(r\) 为第二关键字排序。实际中还有奇偶性优化的排序。块长仍然取 \(\sqrt n\) 即可。
2.1.2 代码
以 小 Z 的袜子 为例题，给出代码：
#include <bits/stdc++.h>
#define MAXN 50010
using namespace std;
typedef long long LL;
const int INF = 2e9;
LL n, a[MAXN], m, bel[MAXN], sq;
struct node{
LL l, r, id;
}q[MAXN];
struct node1{
LL x, y;
}ans[MAXN];
bool cmp(node x, node y)
{
if(bel[x.l] != bel[y.l]) return bel[x.l] < bel[y.l];
if(bel[x.l] & 1) return x.r < y.r;
return x.r > y.r;
}
LL cnt, tot[MAXN];
void add(int p)
{
int x = a[p];
tot[x]++;
if(tot[x] > 1) cnt += (tot[x] - 1);
}
void del(int p)
{
int x = a[p];
tot[x]--;
if(tot[x] >= 1) cnt -= tot[x];
}
int main(){
ios::sync_with_stdio(0);
cin >> n >> m;
sq = sqrt(n);
for(int i = 1; i <= n; i++)
{
cin >> a[i];
bel[i] = i / sq + 1;
}
for(int i = 1; i <= m; i++)
{
cin >> q[i].l >> q[i].r;
q[i].id = i;
}
sort(q + 1, q + m + 1, cmp);
int l = 1, r = 0;
for(int i = 1; i <= m; i++)
{
while(l < q[i].l) del(l++);
while(r > q[i].r) del(r--);
while(l > q[i].l) add(--l);
while(r < q[i].r) add(++r);
ans[q[i].id].x = cnt;
ans[q[i].id].y = (q[i].r - q[i].l + 1) * (q[i].r - q[i].l) / 2;
}
for(int i = 1; i <= m; i++)
{
if(ans[i].x == 0 || ans[i].y == 0)
{
cout << "0/1" << endl;
continue;
}
int xx = ans[i].x / __gcd(ans[i].x, ans[i].y);
int yy = ans[i].y / __gcd(ans[i].x, ans[i].y);
cout << xx << '/' << yy << endl;
}
return 0;
}
2.2 带修莫队
2.2.1 基础思想
普通莫队是不能修改的。
我们给他强行加上一位时间维，同时记录每个时间所进行的操作。
这样在莫队转移的时候，我们只需要同时修改时间维即可。注意这个操作也要 \(O(1)\) 完成。
但是带修莫队有非常特殊的一点：为了达到最优时间复杂度，我们的块长要取到 \(n^{\frac 23}\)，复杂度为 \(O(n^{\frac 53})\)。
2.2.2 代码
以 数颜色 / 维护队列 为例，给出代码：
#include <bits/stdc++.h>
#define MAXN 1000010
using namespace std;
typedef long long LL;
const int INF = 2e9;
int n, m, bl, cnt1, cnt2, a[MAXN], bel[MAXN], ans[MAXN];
struct node{
int l, r, id, t;
}q[MAXN];
struct node2{
int p, col;
}q2[MAXN];
int cnt, tot[MAXN];
bool cmp(node x, node y)
{
if(bel[x.l] != bel[y.l]) return bel[x.l] < bel[y.l];
if(bel[x.r] != bel[y.r]) return bel[x.r] < bel[y.r];
return x.t < y.t;
}
void add(int x)
{
int p = a[x];
if(tot[p] == 0) cnt++;
tot[p]++;
}
void del(int x)
{
int p = a[x];
tot[p]--;
if(tot[p] == 0) cnt--;
}
void change(int i, int x)
{
if(q2[x].p >= q[i].l && q2[x].p <= q[i].r)
{
del(q2[x].p);
if(tot[q2[x].col] == 0) cnt++;
tot[q2[x].col]++;
}
swap(a[q2[x].p], q2[x].col);
}
int main(){
ios::sync_with_stdio(false);
cin >> n >> m;
bl = pow(n, 2.0 / 3.0);
for(int i = 1; i <= n; i++)
{
cin >> a[i];
bel[i] = i / bl + 1;
}
for(int i = 1; i <= m; i++)
{
string op;
int x, y;
cin >> op >> x >> y;
if(op[0] == 'Q')
{
q[++cnt1].l = x;
q[cnt1].r = y;
q[cnt1].id = cnt1;
q[cnt1].t = cnt2;
}
else
{
q2[++cnt2].p = x;
q2[cnt2].col = y;
}
}
sort(q + 1, q + cnt1 + 1, cmp);
int l = 1, r = 0, t = 0;
for(int i = 1; i <= cnt1; i++)
{
while(l < q[i].l) del(l++);
while(r > q[i].r) del(r--);
while(l > q[i].l) add(--l);
while(r < q[i].r) add(++r);
while(t < q[i].t) change(i, ++t);
while(t > q[i].t) change(i, t--);
ans[q[i].id] = cnt;
}
for(int i = 1; i <= cnt1; i++)
{
cout << ans[i] << endl;
}
return 0;
}
2.3 树上莫队
2.3.1 基础思想
对于一个在树上的问题，我们可以将他转化为序列上的问题。
考虑使用欧拉序，例如对于下面这棵树：
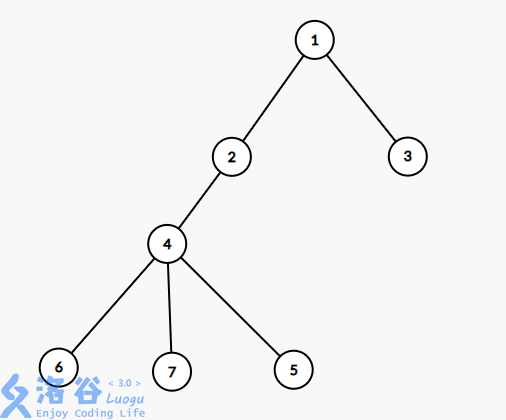
其欧拉序为：\(1,2,4,5,5,6,6,7,7,4,2,3,3,1\)。
这样我们可以将树上的问题转化为序列上的问题。
下面直接看一道例题。
2.3.2 树上莫队实例
以 COT2 - Count on a tree II 为例。
Problem：
求出树上两点间不同颜色的数量。
Solution：
我们还是以 2.3.1 中的树为例。
我们先假设 \(st[u]<st[v]\)。
- 当查询的 \(u,v\) 满足 \(lca(u,v)=u\) ，例如 \(u=2,v=6\)，我们在欧拉序中取出 \([st_2,st_6]\) 区间为 \((2,4,5,5,6)\) 。在这个区间中，\(5\) 出现了两次，因此它并不属于这条链；其余的所有数字就是这条链上的数字 \((2,4,6)\)。
- 当查询的 \(u,v\) 不满足 \(lca(u,v)=u\) 时，例如 \(u=5,v=3\)，我们在欧拉序中取出 \([ed_5,st_3]\) 区间为 \((5,6,6,7,7,4,2,3)\)，将出现两次的数仍然去掉，可以得到 \((5,4,2,3)\)。然而我们也发现，此时 \(lca(u,v)\) 不一定被统计上，因此在这时要特判 \(lca(u,v)\)。
至于如何维护，直接拿树剖就行了，方便快捷。
Code：
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int Maxn = 2e5 + 5;
int n, m;
int a[Maxn], t[Maxn];
int head[Maxn], edgenum;
struct node{
int nxt, to;
}edge[Maxn];
void add_edge(int from, int to) {
edge[++edgenum].nxt = head[from];
edge[edgenum].to = to;
head[from] = edgenum;
}
int dep[Maxn], fa[Maxn], st[Maxn], ed[Maxn], siz[Maxn], son[Maxn], top[Maxn], cnt, rnk[Maxn];
void dfs1(int u) {
son[u] = -1;
siz[u] = 1;
st[u] = ++cnt;
rnk[cnt] = u;
for(int i = head[u]; i; i = edge[i].nxt) {
int to = edge[i].to;
if(to == fa[u]) continue;
dep[to] = dep[u] + 1;
fa[to] = u;
dfs1(to);
siz[u] += siz[to];
if(son[u] == -1 || siz[to] > siz[son[u]]) {
son[u] = to;
}
}
ed[u] = ++cnt;
rnk[cnt] = u;
}
void dfs2(int u, int v) {
top[u] = v;
if(son[u] == -1) return ;
dfs2(son[u], v);
for(int i = head[u]; i; i = edge[i].nxt) {
int to = edge[i].to;
if(to != fa[u] && to != son[u]) {
dfs2(to, to);
}
}
}
int Lca(int u, int v) {
while(top[u] != top[v]) {
if(dep[top[u]] > dep[top[v]]) swap(u, v);
v = fa[top[v]];
}
return dep[u] > dep[v] ? v : u;
}
int sq, bel[Maxn];
struct node1 {
int l, r, id, lca;
bool operator < (const node1 &b) const {
if(bel[l] != bel[b.l]) return bel[l] < bel[b.l];
if(bel[l] & 1) return r < b.r;
return r > b.r;
}
}q[Maxn];
bool vis[Maxn];
int tot, num[Maxn];
void add(int p) {
int x = a[p];
if(vis[p]) {
num[x]--;
if(num[x] == 0) tot--;
}
else {
num[x]++;
if(num[x] == 1) tot++;
}
vis[p] ^= 1;
}
int ans[Maxn];
int main() {
// freopen("1.in", "r", stdin);
// freopen("1.txt", "w", stdout);
ios::sync_with_stdio(0);
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> a[i];
t[i] = a[i];
}
sort(t + 1, t + n + 1);
int p = unique(t + 1, t + n + 1) - t - 1;
for(int i = 1; i <= n; i++) {
a[i] = lower_bound(t + 1, t + p + 1, a[i]) - t;
// cout << a[i] << '\n';
}
for(int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
add_edge(u, v);
add_edge(v, u);
}
dep[1] = 1;
dfs1(1);
dfs2(1, 1);
for(int i = 1; i <= m; i++) {
int u, v, lca;
cin >> u >> v;
if(st[u] > st[v]) swap(u, v);
lca = Lca(u, v);
q[i].lca = lca;
if(lca == u) {
q[i].l = st[u];
q[i].r = st[v];
q[i].lca = 0;
}
else {
q[i].l = ed[u];
q[i].r = st[v];
}
q[i].id = i;
}
sq = sqrt(2 * n);
for(int i = 1; i <= 2 * n; i++) {
bel[i] = i / sq + 1;
}
sort(q + 1, q + m + 1);
int l = 1, r = 0;
for(int i = 1; i <= m; i++) {
while(l > q[i].l) add(rnk[--l]);
while(r < q[i].r) add(rnk[++r]);
while(l < q[i].l) add(rnk[l++]);
while(r > q[i].r) add(rnk[r--]);
if(q[i].lca) {
add(q[i].lca);
}
ans[q[i].id] = tot;
if(q[i].lca) {
add(q[i].lca);
}
}
for(int i = 1; i <= m; i++) {
cout << ans[i] << '\n';
}
return 0;
}
2.3.3 树上带修莫队
树上莫队自然也可以带修，思路与普通莫队的带修一致。这里不再赘述。
可以做一下 [WC2013] 糖果公园。
2.4 回滚莫队
2.4.1 基础思想
在一些问题中，我们会发现，add 和 del 操作通常只有一个可以简单用 \(O(1)\) 维护，另一个则不行。
这种时候，我们就可以使用回滚莫队。其具体思想是：利用回滚处理另一个不好完成的操作，这样只需要完成好完成的操作即可。
这里需要给出回滚莫队的基本步骤：
- 首先按普通莫队排序。
- 如果当前询问的左端点块发生变化，设其为 \(B\)。则将当前左端点设为 \(B\) 块右端点加一，右端点设为 \(B\) 块右端点。
- 如果询问左右端点在同一个块内，暴力求出答案。
- 否则，不断扩展右端点和左端点直到达到询问区间，回答询问。
- 回滚左指针，撤销左指针移动带来的改动。
2.4.2 代码
不想写了，给一个 oi-wiki 上的板子（格式化了）：
//AT_joisc2014_c 歴史の研究
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int n, q;
int x[N], t[N], m;
struct Query {
int l, r, id;
} Q[N];
int pos[N], L[N], R[N], sz, tot;
int cnt[N], __cnt[N];
ll ans[N];
bool cmp(const Query &A, const Query &B) {
if (pos[A.l] == pos[B.l])
return A.r < B.r;
return pos[A.l] < pos[B.l];
}
void build() {
sz = sqrt(n);
tot = n / sz;
for (int i = 1; i <= tot; i++) {
L[i] = (i - 1) * sz + 1;
R[i] = i * sz;
}
if (R[tot] < n) {
++tot;
L[tot] = R[tot - 1] + 1;
R[tot] = n;
}
}
void Add(int v, ll &Ans) {
++cnt[v];
Ans = max(Ans, 1LL * cnt[v] * t[v]);
}
void Del(int v) {
--cnt[v];
}
int main() {
scanf("%d %d", &n, &q);
for (int i = 1; i <= n; i++)
scanf("%d", &x[i]), t[++m] = x[i];
for (int i = 1; i <= q; i++)
scanf("%d %d", &Q[i].l, &Q[i].r), Q[i].id = i;
build();
// 对询问进行排序
for (int i = 1; i <= tot; i++)
for (int j = L[i]; j <= R[i]; j++)
pos[j] = i;
sort(Q + 1, Q + 1 + q, cmp);
// 离散化
sort(t + 1, t + 1 + m);
m = unique(t + 1, t + 1 + m) - (t + 1);
for (int i = 1; i <= n; i++)
x[i] = lower_bound(t + 1, t + 1 + m, x[i]) - t;
int l = 1, r = 0, last_block = 0, __l;
ll Ans = 0, tmp;
for (int i = 1; i <= q; i++) {
// 询问的左右端点同属于一个块则暴力扫描回答
if (pos[Q[i].l] == pos[Q[i].r]) {
for (int j = Q[i].l; j <= Q[i].r; j++)
++__cnt[x[j]];
for (int j = Q[i].l; j <= Q[i].r; j++)
ans[Q[i].id] = max(ans[Q[i].id], 1LL * t[x[j]] * __cnt[x[j]]);
for (int j = Q[i].l; j <= Q[i].r; j++)
--__cnt[x[j]];
continue;
}
// 访问到了新的块则重新初始化莫队区间
if (pos[Q[i].l] != last_block) {
while (r > R[pos[Q[i].l]])
Del(x[r]), --r;
while (l < R[pos[Q[i].l]] + 1)
Del(x[l]), ++l;
Ans = 0;
last_block = pos[Q[i].l];
}
// 扩展右端点
while (r < Q[i].r)
++r, Add(x[r], Ans);
__l = l;
tmp = Ans;
// 扩展左端点
while (__l > Q[i].l)
--__l, Add(x[__l], tmp);
ans[Q[i].id] = tmp;
// 回滚
while (__l < l)
Del(x[__l]), ++__l;
}
for (int i = 1; i <= q; i++)
printf("%lld\n", ans[i]);
return 0;
}
