基础字符串算法

合集 - 学习笔记(52)

1.随机化算法2024-02-27 2.组合数学2024-02-27 3.概率和期望2024-02-27 4.树链剖分2024-02-27 5.矩阵乘法与矩阵快速幂2024-02-27 6.最短路2024-02-27 7.卡特兰数、Prüfer 序列、BSGS2024-02-27 8.分块和莫队2024-02-27 9.AC 自动机2024-02-27 10.平衡树2024-02-27

11.基础字符串算法2024-02-27

12.基础数论2024-02-27 13.Miller-Rabin 与 Pollard-Rho2024-08-23 14.广义后缀自动机2024-06-25 15.后缀自动机 SAM2024-06-22 16.回文自动机 PAM2024-06-18 17.Manacher2024-06-16 18.后缀数组2024-06-08 19.01 分数规划2024-06-02 20.网络流2024-05-05 21.整体二分2024-05-05 22.cdq 分治2024-05-04 23.点分治2024-04-21 24.虚树2024-04-14 25.扫描线2024-04-11 26.笛卡尔树2024-04-06 27.基环树2024-04-02 28.树哈希2024-03-09 29.莫比乌斯反演2024-11-28 30.二分图2024-11-07 31.朱刘算法2024-10-29 32.最大团2024-10-29 33.杂项2024-08-24 34.杜教筛2024-12-01 35.拉格朗日插值2024-12-10 36.线段树综合2024-12-17 37.可持久化数据结构2024-12-24 38.K-D Tree2024-12-25 39.Burnside 引理与 Polya 定理2024-12-27 40.线性基2024-12-30 41.替罪羊树01-09 42.LCT01-18 43.插头 dp01-20 44.原根01-20 45.多项式乘法01-22 46.斯特林数01-23 47.二项式反演与斯特林反演01-23 48.Min-Max 容斥01-24 49.辛普森积分法01-25 50.Min_25 筛02-03 51.凸包02-16 52.2-SAT03-03

1 哈希

1.1 概念

哈希就是构造一个数字使之唯一的代表一个字符串。

我们来考虑一下二进制数的转化：

$(1001)_{2} = 1 \times 2^{3} + 0 \times 2^{2} + 0 \times 2^{1} + 1 = (9)_{10}$

现在，我们令 $^{'} a^{'} = 1,^{'} b^{'} = 2,^{'} c^{'} = 3 \dots,^{'} z^{'} = 26$ 。然后将进制 $p$ 设为 $131$ 。就能得到：

$(a b c)_{p} = 1 \times p^{2} + 2 \times p + 3 = (2248356)_{10}$

这个过程就叫做字符串哈希。

在实际应用中，哈希常常用来判断字符串是否相等。然而，在有些情况下，难免会有两个不同字符串哈希值相等，我们的程序就会爆掉。因此，在正常情况下，通常取 $p = 131, 13331$ 等素数，而且还需要取模，模数一般取 $2^{64} - 1$ 。

1.2 实现

1.2.1 单哈希

我们设 hash[i] 为字符串前 $i$ 位的哈希值。则有递推公式：

hash[i] = hash[i - 1] * p + s[i] - 47

由于模数取 $2^{64} - 1$ ，因此可以用 unsigned long long 类型的自然溢出来达到取模的效果。

代码：

string s;
ull h[Maxn];//注意 c++14 中 "hash" 是关键字
const ull p = 131;

void Hash() {
	for(int i = 1; i <= s.size(); i++) {
		h[i] = h[i - 1] * p + (s[i] - 'a' + 1);
	}
}

1.2.2 双哈希

由于一个哈希仍仍可能被毒瘤出题人卡掉，我们可以对一个字符串用两个 $q$ 计算，只有两个哈希都相等时才满足。这被称之为双哈希，几乎不可能再有错误概率。

如下：

string s;
ll h1[Maxn], h2[Maxn];
const ll p = 131;
const ll q1 = 998244353;
const ll q2 = 1000000007;

void Hash() {
	for(int i = 1; i <= s.size(); i++) {
		h1[i] = (h1[i - 1] * p % q1 + (s[i] - 'a' + 1) % q1) % q1;
		h2[i] = (h2[i - 1] * p % q2 + (s[i] - 'a' + 1) % q2) % q2;
	}
}

1.3 基本应用

1.3.1 获取字串哈希

我们举一个浅显的例子：

设一个字符串为 $s_{1} s_{2} s_{3} s_{4}$ 。

则哈希值分别如下：

$h a s h [1] = s_{1}$

$h a s h [2] = s_{1} \times p + s_{2}$

$h a s h [3] = s_{1} \times p^{2} + s_{2} \times p + s_{3}$

$h a s h [4] = s 1 \times p^{3} + s_{2} \times p^{2} + s_{3} \times p + s_{4}$

假如我们要知道 $s_{3} s_{4}$ 的哈希值，也就是 $s_{3} \times p + s_{4}$ ，应该怎么算呢？

很明显，用 $h a s h [4]$ 和 $h a s h [2]$ 得到，但 $h a s h [2]$ 差了一个 $p^{2}$ ，我们就给他乘上，所以结果为：

$h a s h [4] - h a s h [2] \times p^{2}$

这启示我们一个重要的公式：

一个字符串 $| S |$ ，其字串 $s_{l} \dots s_{r}$ 的哈希值的为：

$h a s h [r] - h a s h [l - 1] \times p^{r - l + 1}$

注意实际应用中的取模。

1.3.2 一些应用

首先，有一句不知道谁说的话：

哈希可以当半个 KMP、Manacher 等其他字符串算法使用。

1.3.2.1 字符串匹配

这个其实很好做了，求出文本串中每个与模式串长度相等的串的哈希，比较即可。

1.3.2.2 允许至多 $k$ 次失配的字符串匹配

这道题无法使用 KMP 解决，但是可以通过哈希 + 二分来解决。

枚举所有可能匹配的子串，假设现在枚举的子串为 $s^{'}$ ，通过哈希 + 二分可以快速找到 $s^{'}$ 与 $p$ 第一个不同的位置。之后将 $s^{'}$ 与 $p$ 在这个失配位置及之前的部分删除掉，继续查找下一个失配位置。这样的过程最多发生 $k$ 次。

总的时间复杂度为 $O (m + k b \log_{2} m)$ 。

1.3.2.3 最长回文子串

这就体现出半个 Manacher 的好处了。

二分答案，判断可行时枚举回文中心（对称轴），哈希来判断来两侧是否相等。需要正着和倒着都处理一遍哈希，复杂度 $O (n \log n)$ 。

（其实哈希就可以当 Manacher 使用，有一种 $O (n)$ 的哈希回文，具体看 OI Wiki）

2 KMP

2.1 问题概述

这个算法是一种在文本串 $s$ 中查找模式串 $p$ 的算法。

我们先想一下暴力算法会怎么做：

int i = 0, j = 0;
while (i < s.size())
{
    if (s[i] == p[j])
        ++i, ++j;
    else
        i = i - j + 1, j = 0;
    if (j == p.length())  // 匹配成功
    {
        cout << i - j << endl;
        i = i - j + 1;
        j = 0;
    }
}

在暴力匹配中，我们定义了两个指针 $i$ 和 $j$ ，分别在 $s$ 和 $p$ 上。每次 $i$ 与 $j$ 失配时， $i, j$ 都要回溯至起始点重新匹配。复杂度 $O (n m)$ 。

由于每次失配时， $i, j$ 都要回溯至起始点重新匹配，这样大大浪费了时间。我们考虑将 $i$ 定住，不让 $i$ 回溯。现在的问题是： $j$ 如何转移？

2.2 KMP 算法

2.2.1 PMT 表

$j$ 如何转移，至于模式串 $p$ 有关。每个模式串都有一个 PMT。我们定义 pmt[i] 表示前 $i$ 位中公共真前后缀的长度。通俗来讲就是从 $p_{0}$ 往后， $p_{i}$ 往前数，保证相同的情况下最多能数多少位。

例如：

下标	0	1	2	3	4	5	6	7	8
`p[i]`	a	b	a	b	c	a	b	a	a
`pmt[i]`	0	0	1	2	0	1	2	3	1

接下来，我们先不管 pmt[i] 如何求，我们先来考虑一下 PMT 对于 $j$ 转移的作用。

我们来看下面两个字符串：

a	b	a	b	a	b	c	a	b
a	b	a	b	c

我们来看第 $5$ 格，此时失配，我们保持 $i$ 不变。由于 abab 已经匹配成功，同时有公共前后缀 ab，我们把它利用起来，变成这样：

a	b	a	b	a	b	c	a	b
		a	b	a	b	c

我们就充分利用到了之前的结果。这里实际上就是进行 j=pmt[j-1] 操作。

当然，如果一直不匹配，我们要一直让 $j$ 等于 pmt[j-1]，pmt[pmt[j-1]-1]……直到等于 $0$ 。

代码如下：

void KMP(string s, string p) {
	for(int i = 0, j = 0; i < s.size(); i++) {
		while(j && s[i] != p[j]) j = pmt[j - 1];
		if(s[i] == p[j]) j++;
		if(j == p.size()) {
			//do something...
			j = pmt[j - 1];
		}
	}
}

2.2.2 求 PMT

上面已经讲述了如何求解 KMP，但有一个很小的大问题：

如何求出 PMT？

有一个相当精妙的方法：将 $p$ 错开一位后，自己去匹配自己。这其实相当于用前缀来匹配一个公共的后缀。

先令 pmt[0]=0。然后如下：

a	b	a	b	c	a	b	a	a
	a	b	a	b	c	a	b	a	a

第一位匹配失败，pmt[1]=0， $i$ 后移。

a	b	a	b	c	a	b	a	a
		a	b	a	b	c	a	b	a	a

匹配成功，则 $j$ 指针右移，于是 pmt[2]=1，两个指针均右移。

而后不断重复。其实这段代码与 KMP 过程相当相似：

void PMT(string p) {
	for(int i = 1, j = 0; i < p.size(); i++) {
		while(j && p[i] != p[j]) j = pmt[j - 1];
		if(p[i] == p[j]) j++;
		pmt[i] = j;
	}
}

然后就得到了完整的 KMP 代码。

2.3 完整代码

以 POJ3461 乌力波为例：

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
const int Maxn = 1e6 + 5;

string s, p;
int pmt[Maxn], cnt;

void PMT(string p) {
	for(int i = 1, j = 0; i < p.size(); i++) {
		while(j && p[i] != p[j]) j = pmt[j - 1];
		if(p[i] == p[j]) j++;
		pmt[i] = j;
	}
}

void KMP(string s, string p) {
	for(int i = 0, j = 0; i < s.size(); i++) {
		while(j && s[i] != p[j]) j = pmt[j - 1];
		if(s[i] == p[j]) j++;
		if(j == p.size()) {
			cnt++;
			j = pmt[j - 1];
		}
	}
}

int T;

int main() {
	ios::sync_with_stdio(0);
	cin >> T;
	while(T--) {
		cin >> p >> s;
		cnt = 0;
		PMT(p);
		KMP(s, p);
		cout << cnt << '\n';
	}
	return 0;
}

2.3.1 补充

大多数文章和教材会使用 next[i] 数组，其实就是将 pmt 整体右移一位（令 next[0]=-1）

而上面的算法也只能叫 MP 算法，因为我们还缺少一个由 Knuth 提出的常数优化。但时间复杂度永远是 $O (n + m)$ 。具体可以看这个。

3 Trie

3.1 概念

Trie（字典树）是一个比较好理解的数据结构，用来存储和查询字符串。

如下图，就是一颗由 water，wish，win，tie，tired 组成的字典树。

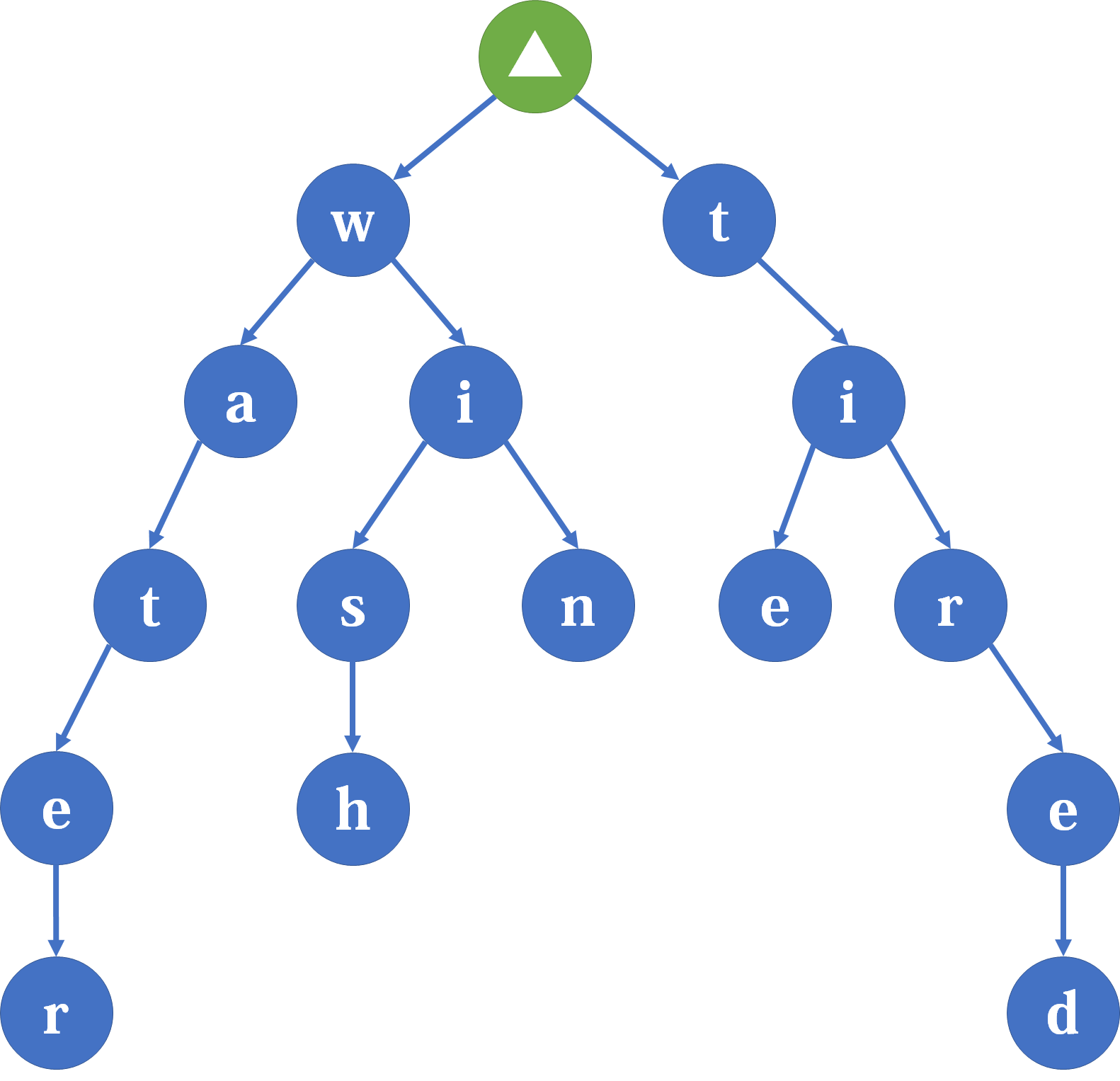
树上的一个节点就是一个字符，树上的一条链就是一个字符串。相同前缀的字符串共用一部分节点。

这样，我们牺牲了一部分空间，实现了 $O (n)$ 的查询。

3.2 实现

3.2.1 建树

考虑建树。用 nxt[i][j] 表示 $i$ 号点的儿子中，存储字符映射值为 $c$ 的节点编号。注意 $1$ 号点一般不放字符，代码如下：

int nxt[Maxn][27], cnt = 1;

void insert(string s) {
	int u = 1;
	for(int i = 0; i < s.size(); i++) {
		int c = s[i] - 'a' + 1;
		if(!nxt[u][c]) {//尽可能重复使用前缀，否则建立新节点
			nxt[u][c] = ++cnt;
		}
		u = nxt[u][c];
	}
}

3.2.2 查询

3.2.2.1 查询前缀

我们可以用字典树简单的查询到一个前缀是否存在。与建树代码比较相似：

bool find(string s) {
	int u = 1;
	for(int i = 0; i < s.size(); i++) {
		int c = s[i] - 'a' + 1;
		if(!nxt[u][c]) {
			return 0;
		}
		u = nxt[u][c];
	}
	return 1;
}

3.2.2.2 查询字符串

如果要查询某个字符串是否出现，就不能够直接判断，因为可能出现一个字符串是另一个的前缀。

我们用一个 vis 数组。在插入操作完成时，把当前叶子结点的 vis 设为 $1$ 。查询完成后判断 vis 是否存在即可。

这是一个常见的套路，在 Trie 中用叶子结点代表整个字符串，来保存信息已完成要求。

3.2.3 模板

以 P8306 【模板】字典树 - 洛谷为例。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int Maxn = 4e6 + 5;

int nxt[Maxn][65], cnt = 1, vis[Maxn];

void insert(string s) {
	int u = 1;
	for(int i = 0; i < s.size(); i++) {
		int c;
		if(s[i] >= '0' && s[i] <= '9') c = s[i] - '0' + 1;
		if(s[i] >= 'A' && s[i] <= 'Z') c = s[i] - 'A' + 11;
		if(s[i] >= 'a' && s[i] <= 'z') c = s[i] - 'a' + 38;
		if(!nxt[u][c]) {
			nxt[u][c] = ++cnt;
		}
		u = nxt[u][c];
		vis[u] ++;
	}
}

int find(string s) {
	int u = 1;
	for(int i = 0; i < s.size(); i++) {
		int c;
		if(s[i] >= '0' && s[i] <= '9') c = s[i] - '0' + 1;
		if(s[i] >= 'A' && s[i] <= 'Z') c = s[i] - 'A' + 11;
		if(s[i] >= 'a' && s[i] <= 'z') c = s[i] - 'a' + 38;
		if(!nxt[u][c]) {
			return 0;
		}
		u = nxt[u][c];
	}
	return vis[u];
} 

int T;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> T;
	while(T--){
		int n, q;
		cin >> n >> q;
		for(int i = 1; i <= cnt; i++) {//卡 memset 了 
			memset(nxt[i], 0, sizeof(nxt[i]));
			vis[i] = 0;
		}
		cnt = 1;
		for(int i = 1; i <= n; i++) {
			string s;
			cin >> s;
			insert(s);
		}
		for(int i = 1; i <= q; i++) {
			string t;
			cin >> t;
			cout << find(t) << '\n';
		}
	}
	return 0;
}

3.3 0-1 Trie

3.3.1 概念

01-Trie，是一种用 Trie 来存储数字二进制的数据结构，常常被用来求解数字异或问题。

我们将原本 Trie 的字符集缩减为只有 ${0, 1}$ ，将原先字符串变为一个个二进制数，以此来建树。这样我们得到的 Trie 树就叫做 01-Trie。

3.3.2 建树

建树与普通 Trie 没有什么区别，到位了做题方便，一般还用 num 来记录当前叶子结点所对应的数字（又是上面的小技巧）。

int nxt[Maxn][2], cnt = 1, num[Maxn];

void insert(int x) {
    int u = 1;
	for(int i = 30; i >= 0; i--) {//枚举可能的位数 
		int c = x >> i & 1;//取出 x 的第 i 位
		if(!nxt[u][c]) {
			nxt[u][c] = ++ cnt;
		} 
		u = nxt[u][c];
	}
	num[u] = x;
}

3.3.3 具体应用及代码

3.3.3.1 最大异或对

以 The XOR Largest Pair 为例。

题目大意：在 $n$ 个数中选出两个数，使他们的异或和最大。

我们先建立 01-Trie，然后使用贪心求解。枚举当前的数 $a_{i}$ ，在树上走一条路径。由于要求异或和最大，所以要尽可能让当前位上的数与 $a_{i}$ 当前位上的数不一样，否则就只能走相同的了。

同时，依次为模板题，给出 01-Trie 代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int Maxn = 2e5 + 5;

int nxt[Maxn][2], cnt = 1, num[Maxn];

void insert(int x) {
	int u = 1;
	for(int i = 30; i >= 0; i--) {//枚举可能的位数 
		int c = x >> i & 1;//取出 x 的第 i 位
		if(!nxt[u][c]) {
			nxt[u][c] = ++ cnt;
		} 
		u = nxt[u][c];
	}
	num[u] = x;
} 

int find(int x) {
	int u = 1;
	for(int i = 30; i >= 0; i--) {
		int c = x >> i & 1;
		if(nxt[u][c ^ 1]) {//尽量不同 
			u = nxt[u][c ^ 1];
		}
		else {
			u = nxt[u][c];
		}
	}
	return x ^ num[u];//返回异或值 
} 

int n, a[Maxn], ans;

int main() {
	ios::sync_with_stdio(0);
	cin >> n;
	for(int i = 1; i <= n; i++) {
		cin >> a[i];
		insert(a[i]);
	}
	for(int i = 1; i <= n; i++) {
		ans = max(ans, find(a[i]));//枚举取最大 
	}
	cout << ans;
	return 0;
}

3.3.3.2 最大异或路径

以 The XOR-longest Path 为例。

题目大意：给定一棵 $n$ 个点的带权树，求树上最长的异或和路径。

由于异或具有一个特点： $a xor a = 0$ ，所以，设 $t_{i}$ 为从根节点到点 $i$ 的异或和，那么对于树上两点 $A, B$ ，他们的路径异或和就是 $t_{A} xor t_{B}$ ，因为 $t_{L C A}$ 部分被算了两次，抵消了。

而此时我们再看，在 $n$ 个结点的 $t_{i}$ 中，选出两个数的最大异或和。这非常熟悉，实际上就是 3.3.3.1 的情况。

代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int Maxn = 2e6 + 5;

int n;
int head[Maxn], edgenum;
struct node{
	int nxt, to, w;
}edge[Maxn];

void add_edge(int from, int to, int w) {
	edge[++edgenum].nxt = head[from];
	edge[edgenum].to = to;
	edge[edgenum].w = w;
	head[from] = edgenum;
}

int t[Maxn];
void dfs(int x, int fa, int val) {
	t[x] = t[fa] ^ val;
	for(int i = head[x]; i; i = edge[i].nxt) {
		int to = edge[i].to;
		if(to == fa) continue;
		dfs(to, x, edge[i].w); 
	}
}

int nxt[Maxn][2], cnt = 1, num[Maxn];

void insert(int x) {
	int u = 1;
	for(int i = 30; i >= 0; i--) {
		int c = x >> i & 1;
		if(!nxt[u][c]) {
			nxt[u][c] = ++cnt;
		}
		u = nxt[u][c];
	}
	num[u] = x;
}

int find(int x) {
	int u = 1; 
	for(int i = 30; i >= 0; i--) {
		int c = x >> i & 1;
		if(nxt[u][c ^ 1]) {
			u = nxt[u][c ^ 1];
		}
		else {
			u = nxt[u][c];
		}
	}
	return x ^ num[u];
}

int ans = 0;

int main() {
	ios::sync_with_stdio(0);
	cin >> n;
	for(int i = 1; i < n; i++) {
		int u, v, w;
		cin >> u >> v >> w;
		add_edge(u, v, w);
		add_edge(v, u, w);
	}
	dfs(1, 0, 0);
	for(int i = 1; i <= n; i++) {
		insert(t[i]);
	}
	for(int i = 1; i <= n; i++) {
		ans = max(ans, find(t[i]));
	}
	cout << ans;
	return 0;
}

posted @ 2024-02-27 17:53 UKE_Automation 阅读(26) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· AC 自动机

· 提高组字符串专题做题记录

· 「学习笔记」字符串基础：Hash，KMP与Trie

· 笔记——字符串

· 字符串算法学习笔记

阅读排行：
· 震惊！C++程序真的从main开始吗？99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码？零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾（3.3-3.9）
· winform 绘制太阳，地球，月球运作规律

公告

昵称： UKE_Automation
园龄： 1年1个月
粉丝： 17
关注： 7

+加关注

2025年3月

日

一

二

三

四

五

六

UKE_Automation