矩阵乘法与矩阵快速幂
1 矩阵乘法
1.1 定义
对于两个矩阵 \(A,B\)，其中 \(A\) 大小为 \(n\times m\) ，\(B\) 大小为 \(m\times p\)，则这两个矩阵可以做乘法，得到的矩阵 \(C\) 的大小为 \(n\times p\)。
例如：
\( A=\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{bmatrix}\)
\( B=\begin{bmatrix} b_{11} & b_{12}\\ b_{21} & b_{22}\\ b_{31} & b_{32} \end{bmatrix} \)
则有：
1.2 注意点
- 只有当矩阵 \(A,B\) 满足 \(A\) 的列数等于 \(B\) 的行数时，才能进行矩阵乘法。
- 矩阵乘法不满足交换律（这点很重要）
1.3 代码
提供一个封装模板。
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef long long LL;
const int Maxn = 205;
int n, m, p;
struct matrix {
int n, m, p[Maxn][Maxn];
matrix operator * (const matrix &b) const {
matrix a = *this, c;
c.n = a.n, c.m = b.m;
for(int i = 1; i <= a.n; i++) {
for(int j = 1; j <= a.m; j++) {
for(int k = 1; k <= b.m; k++) {
c.p[i][k] += a.p[i][j] * b.p[j][k];
}
}
}
return c;
}
void print() {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cout << p[i][j] << " ";
}
cout << '\n';
}
}
}A, B, C;
signed main() {
ios::sync_with_stdio(0);
cin >> n >> m;
A.n = n, A.m = m;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cin >> A.p[i][j];
}
}
cin >> p;
B.n = m, B.m = p;
for(int i = 1; i <= m; i++) {
for(int j = 1; j <= p; j++) {
cin >> B.p[i][j];
}
}
C = A * B;
C.print();
return 0;
}
2 矩阵快速幂
2.1 定义
仿照着数字的快速幂，我们也能快速求出矩阵的幂。
定义矩阵的幂为：\(A^n=A\cdot A\cdot A\cdot A\cdots\)
这很明显需要满足原矩阵为正方形。
2.2 用途
矩阵快速幂的经典应用就是加速递推。
直接举几个例子。
2.2.1 「例 1」Fibonacci 第 n 项
Problem
求斐波那契数列第 \(n\) 项后四位（\(n\le10^9\)）
Solution
第一眼：这不是递推板题吗！
然而 \(n\le10^9\)，\(O(n)\) 暴力绝对爆炸。
我们运用矩阵快速幂加速递推。
接下来我们来求一下递推式（注意掌握方法）：
\(①\) 我们先来写出 \(F_n\) 的部分：
\(②\) 接下来我们关注右边的第二个矩阵，发现他们的下标相差 \(1\)，因此左边的矩阵应该是 \(\begin{bmatrix} F_n \\ F_{n-1} \end{bmatrix}\) 。
\(③\) 最后补全整个式子：
因此我们对于矩阵 \(\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}\) 不断做快速幂，然后乘上 \(\begin{bmatrix} F_{1} \\ F_{0} \end{bmatrix}\) 即可。
Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef long long LL;
const int Maxn = 205;
int n, mod;
struct matrix {
int n, m, p[Maxn][Maxn];
void init() {
n = 0, m = 0, memset(p, 0, sizeof p);
}
matrix operator * (const matrix &b) const {
matrix a = *this, c;
c.init();
c.n = a.n, c.m = b.m;
for(int i = 1; i <= a.n; i++) {
for(int j = 1; j <= a.m; j++) {
for(int k = 1; k <= b.m; k++) {
c.p[i][k] = (c.p[i][k] + a.p[i][j] * b.p[j][k] % mod) % mod;
}
}
}
return c;
}
matrix operator ^ (const int &o) const {
matrix res, a = *this; int b = o;
res.init();
res.n = res.m = 2;
res.p[1][1] = res.p[2][2] = 1;
while(b) {
if(b & 1) {
res = res * a;
}
a = a * a;
b >>= 1;
}
return res;
}
void print() {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cout << p[i][j] << " ";
}
cout << '\n';
}
}
}A;
signed main() {
ios::sync_with_stdio(0);
cin >> n >> mod;
A.p[1][1] = A.p[1][2] = A.p[2][1] = 1;
A.n = A.m = 2;
A = A ^ (n - 1);
cout << A.p[1][1];
return 0;
}
2.2.2 「例 2」P207 迷路
Solution
我们发现如果边权为 \(1\) ，那么直接将矩阵 \(T\) 次方即可。
但是此时边权不为 \(1\)，所以不能这样做。
但是我们又会发现这个边权居然最高才 \(9\)，因此我们考虑一下分层图的思路。
将一个点拆成 \(9\) 个点并顺次相连，这样能将边权转化为 \(1\)。举个例子：
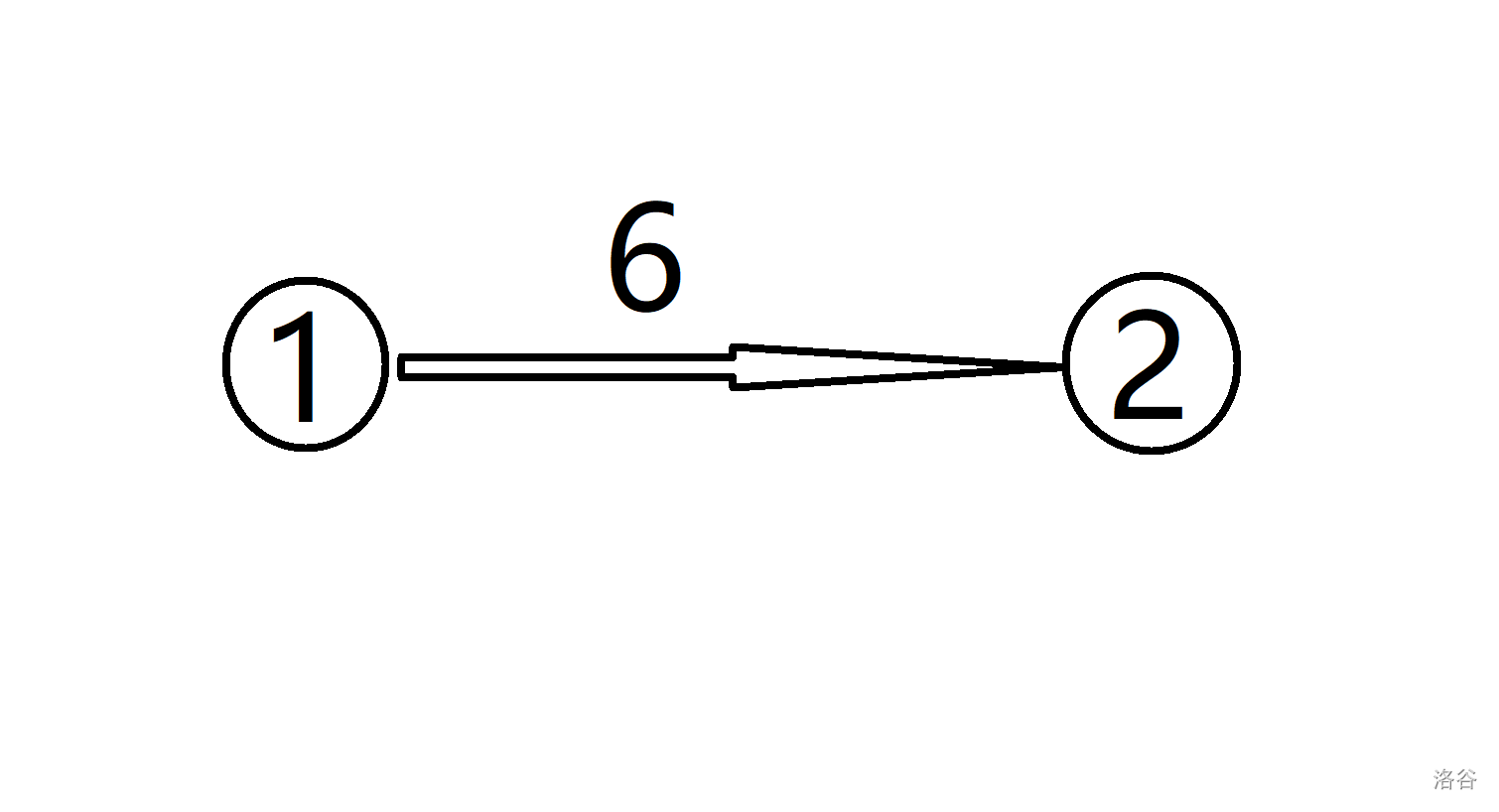
对于这样一条边，我们将 \(1\) 和 \(2\) 两个点拆开，然后将他们按照原先边权连起来，如下图：
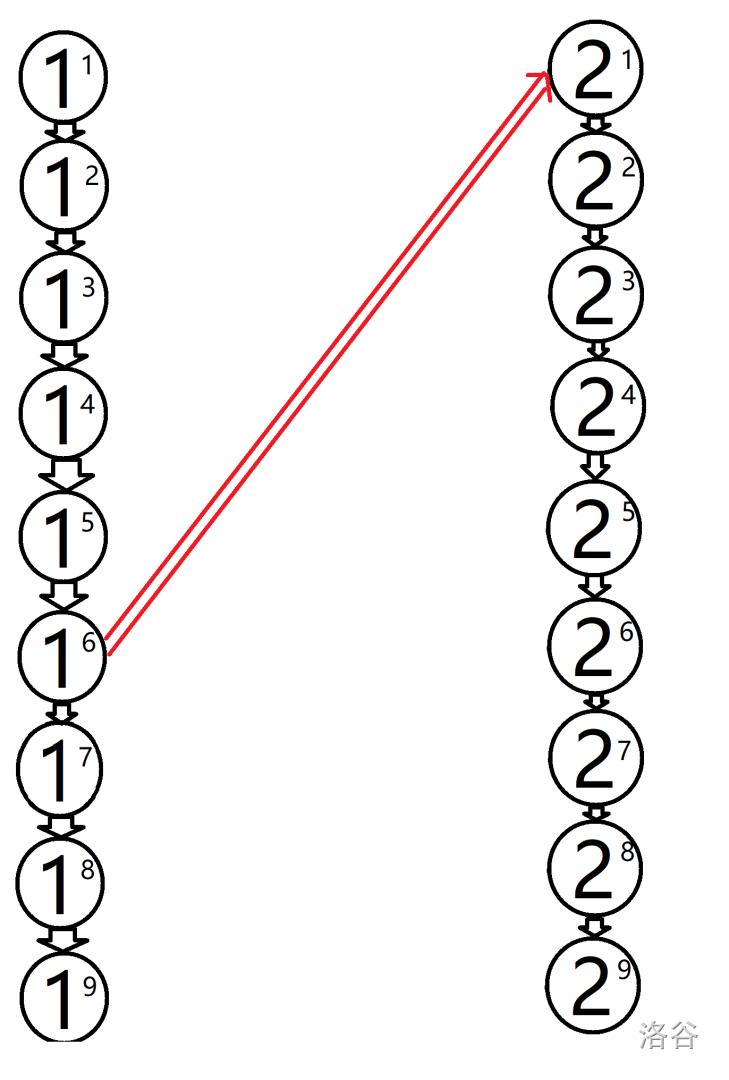
这样从 \(1_1\) 走到 \(2_1\)，经过的边权仍然是 \(6\)，但我们就转化成了边权为 \(1\) 的图。
注意最后统计答案时统计的是点 \(n_1\) 的值而非 \(n\) 的所有值的和。
接下来注意细节即可。
Code
#include <bits/stdc++.h>
/*
我们发现如果边权为 1，那就是一道求 t 次方的大板子题
然而这题有边权，所以不能这么干
我们考虑分层图的思想，既然边权才 9，那我们直接将一个点暴力拆成九个点，然后边权就能转化为 1
这下就是大板子题了，在求 t 次方即可
*/
using namespace std;
typedef long long LL;
const int Maxn = 205;
const int Mod = 2009;
int n, t, m;
struct matrix {
int n, m, p[Maxn][Maxn];
void init() {
n = 0, m = 0, memset(p, 0, sizeof p);
}
matrix operator * (const matrix &b) const {
matrix a = *this, c;
c.init();
c.n = a.n, c.m = b.m;
for(int i = 1; i <= a.n; i++) {
for(int j = 1; j <= a.m; j++) {
for(int k = 1; k <= b.m; k++) {
c.p[i][k] = (c.p[i][k] + a.p[i][j] * b.p[j][k] % Mod) % Mod;
}
}
}
return c;
}
matrix operator ^ (const int &o) const {
matrix res, a = *this; int b = o;
res.init();
res.n = res.m = a.n;
for(int i = 1; i <= n; i++) {
res.p[i][i] = 1;
}
while(b) {
if(b & 1) {
res = res * a;
}
a = a * a;
b >>= 1;
}
return res;
}
void print() {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cout << p[i][j] << " ";
}
cout << '\n';
}
}
}A;
signed main() {
ios::sync_with_stdio(0);
cin >> n >> t;
m = n * 9;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= 8; j++) {
A.p[9 * (i - 1) + j][9 * (i - 1) + j + 1] = 1;
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
char ch;
cin >> ch;
if(ch > '0') {
A.p[9 * (i - 1) + ch - '0'][9 * (j - 1) + 1] = 1;
}
}
}
A.n = A.m = m;
A = A ^ t;
cout << A.p[1][9 * (n - 1) + 1];
return 0;
}
2.2.3 「例 3」佳佳的 Fibonacci
Problem
求 \((F_1+2F_2+3F_3+\cdots+nF_n)\bmod{m}\) 的值。
Solution
我们还是运用矩阵快速幂。
但是我们发现这个形式似曾相识，还记得求区间修改区间查询的 BIT 时候的式子吗？他和这个形式是一样的。
我们还是再来推一遍：
先设 \(S_i=F_1+F_2+\cdots+F_i\)
然后有：
然后我们再令 $P_n=\sum_{i=1}^{n-1}S_i $，则此时原式就可以化为：
接下来我们递推 \(S_n,P_n\) 来得到原式。
还是分步讨论：
\(①\) 写出关于 \(P_n\) 的部分。注意到 \(P_n=P_{n-1}+S_{n-1}\)：
\(\begin{bmatrix} P_n \\ \ \\ \ \\ \ \end{bmatrix}=\begin{bmatrix} 1 & 1 & 0 & 0\\ \ & \ & \ &\ \\ \ & \ & \ &\ \\ \ & \ & \ &\ \end{bmatrix}\begin{bmatrix} P_{n-1} \\ S_{n-1} \\ \ \\ \ \end{bmatrix}\)
\(②\) 注意到右边第二个矩阵要满足 \(S\) 与 \(P\) 下标相等，所以左边还要满足。又注意到 \(S_{n}=S_{n-1}+F_n\)，所以再补全一部分：
\(\begin{bmatrix} P_n \\ S_n \\ \ \\ \ \end{bmatrix}=\begin{bmatrix} 1 & 1 & \ &\ \\ 0 & 1 & 1 &\ \\ \ &\ & \ & \ \\ \ & \ & \ &\ \end{bmatrix}\begin{bmatrix} P_{n-1} \\ S_{n-1} \\ F_n \\ \ \end{bmatrix}\)
\(③\) 又注意到右边 \(F\) 的下标比 \(S\) 的下标多 \(1\)，因此左边应该是 \(F_{n+1}\)。又注意到 \(F_{n+1}=F_n+F_{n-1}\)，所以补全为：
\(\begin{bmatrix} P_n \\ S_n \\ F_{n+1} \\ F_n \end{bmatrix}=\begin{bmatrix} 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1\\ 0 & 0 & 1 & 0 \end{bmatrix}\begin{bmatrix} P_{n-1} \\ S_{n-1} \\ F_n \\ F_{n-1} \end{bmatrix}\)
然后实现即可。
Code
十年 OI 一场空，不开 long long 见祖宗。
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef long long LL;
const int Maxn = 205;
int n, mod;
struct matrix {
int n, m, p[Maxn][Maxn];
void init() {
n = m = 0;
memset(p, 0, sizeof p);
}
void print() {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cout << p[i][j] << " ";
}
cout << '\n';
}
}
matrix operator * (const matrix &b) const {
matrix a = *this, c;
c.init();
c.n = a.n, c.m = b.m;
for(int i = 1; i <= a.n; i++) {
for(int j = 1; j <= a.m; j++) {
for(int k = 1; k <= b.m; k++) {
c.p[i][k] = (c.p[i][k] + a.p[i][j] * b.p[j][k] % mod) % mod;
}
}
}
return c;
}
matrix operator ^ (const int &b) const {
int p = b;
matrix a = *this, res;
res.init();
res.n = res.m = a.n;
for(int i = 1; i <= a.n; i++) {
res.p[i][i] = 1;
}
while(p) {
if(p & 1) {
res = res * a;
}
a = a * a;
p >>= 1;
}
return res;
}
}A, F;
signed main() {
ios::sync_with_stdio(0);
cin >> n >> mod;
A.init(), F.init();
A.n = A.m = 4;
A.p[1][1] = A.p[1][2] = A.p[2][2] = A.p[2][3] = A.p[3][3] = A.p[3][4] = A.p[4][3] = 1;
F.n = 4, F.m = 1;
F.p[3][1] = 1;
A = A ^ n;
A = A * F;
cout << (n * A.p[2][1] % mod - A.p[1][1] + mod) % mod;
return 0;
}
