线段树是一种优化方法,一般来说,所有的树状数组都可以用线段树来做,但线段树的题目不一定能用树状数组来做。
线段树可以这么理解:
- 其实就是把一组数据用一棵树分割成若干个节点保存。
- 然后,在树中查找所需要的数据即可。
- 即[L,R]区间范围内有n个点分成若干个子区间。
- 通过对这些少量子区间的修改或者统计,来实现快速对[L,R]的修改或者统计
线段树的主要的代码有三种
- 建树(单点,区间)
- 查找(单点,区间)
- 修改
- 标记下传
其实都和树状数组很像,具体的一棵线段树是这样纸的:
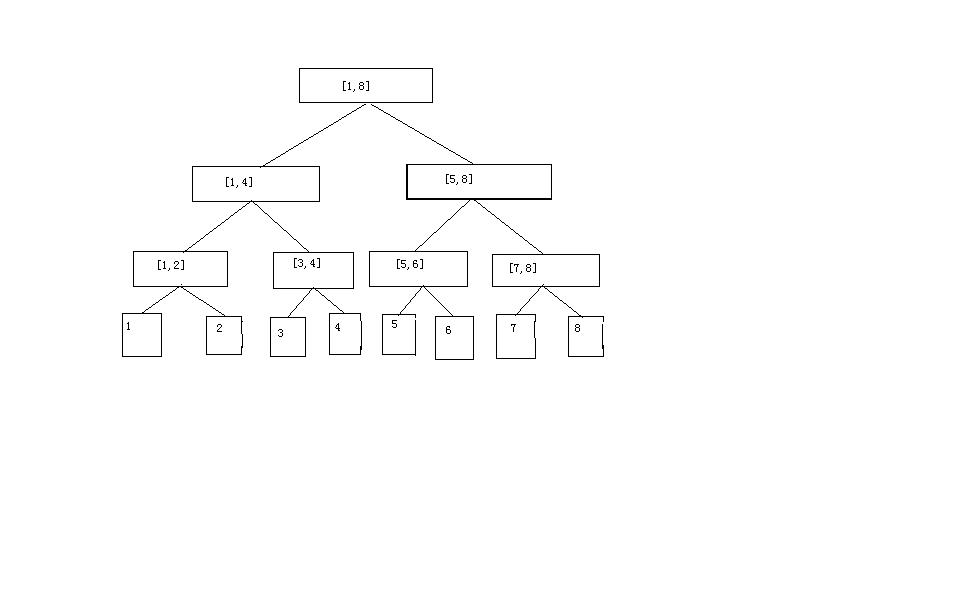
建立线段树的代码是这个样纸的:
void build(int Lchild,int Rchild,int k,int v){ //L,Rchild是指左右儿子;v是指要修改的值 int mid=(Lchild+Rchild)/2;//二分建树 if(Lchild==Rchild){ mi[k]=v;//当然这里也可以这样理解 //scanf("%d",mi[k]);这样应该会更好理解 return ; } build(Lchild,mid,k*2);//建立左子树; build(mid+1,Rchild,k*2+1);//建立右子树; mi[k]=min(mi[k*2],mi[k*2+1]);//mi维护区间最小值 }
然后就是查找:
int query(int l,int r,int k,int x,int y){//查找 if(x>r||y<l)//区间[x,y]没有被[l,r]包含 return 2147483647//则返回一个极大值 if(x<=l&&y>=l)//询问区间在当前区间的值 return mi[k];//返回并维护区间最小值 if(x>=1&&y<=r) return min(query(k*2,mid),query(k*2+1,mid+1,r)); //否则分别处理左右子区间 }
接着是进行修改:
int change(int l,int r,int k,int x,int v){//修改 if(x>r||x<l) return; if(l==r&&l==x){//l==x相当于r==x; mi[k]=v; return; } change(l,mid,k*2,x,v); change(mid+1,k*2+1,x,v);//修改左右子树 mi[k]=min(mi[k*2],mi[k*2+1]);//继续维护区间最小值 }
and 标记下移:
void add(int k,int l,int r,int v){//给区间[l,r]所有的数加上v mi[k]+=v;//打标记 sum[k]+=(r-l+1)*v;//维护对应的区间和 return; } void down(int k){//标记下传 //判断 if(mi[k]==0)//若无标记则不考虑此步操作 return ;//无需返回任何值 add(k*2,l,mid,mi[k]);// 下传到左子树 add(k*2+1,mid+1,r,mi[k]);//下传到右子树 mi[k]=0;//标记清零 }
last 区间修改:
void modify(int k,int l,int r,int x,int y,int v){//给定区间[x,y]所有数加上v; if(x<=l&&y>=r) return add(k,l,r,v); int mid=(l+r>>1); down(k,l,r,mid);//没达到一个节点都需要下传一次标记 if(x<=mid) modify(k*2,l,mid,x,y,v); //修改左子树 if(mid<y) modify(k*2+1,mid+1,r,x,y,v);// 修改右子树 sum[k]=sum[k*2]+sum[k*2+1];//下传后更新sum的值 }
唔,先到这里吧!

