最近在复习小根堆,看了好多博客,一些思想记录一下。
早上自己团队在比赛的时候,第一道题爆零,老师讲是用小根堆解决,所以好好复习了一下小根堆;
首先,小根堆其实就是二叉树。当然,最出名的是一个叫做堆排序的东东,它的时间复杂度为O(nlogn)。足够的小吧,此外它还有一个别名叫做二叉树排序。
赠送团队第一题的链接:
剑与魔法
唔,博主写这题的时候的直接想法是DFS,当然这样是解决不了的,虽然博主不知道为什么解决不了,但是还是将思路留在这里:
我是这么想的,首先输出“-1”的条件是,事件中所有战役事件加起来并没有达到穿越回去事件的RP值,那么老师不仅拿不到金币还回不到过去,这个时候就应该输出“-1”,
然后,就是成立的条件一个“else”,那么老师可以拿到的金币就是各个战役的RP++,首先,因为题面要求老师必须在最后一个返回事件返回,所以无论前面有多少个事件都不能触发,
然而根据题意,穿越回去事件的触发是被动的,只有参与的战役数达到RP时才能穿越,所以搜索所有的战役事件,并且所进行的战役不能超过前面所有的“EOF”事件的RP值,
这就导致了我们要将所有的尝试值存储下来,然后进行对比“Max(dfs(1),dfs(2))”,这样就可以求得每个“EOF”事件之前所获得的金币最大值。
(当然博主不知道为啥一直调试不出来,希望能有位大佬帮助一下蒟蒻(逃)
其次,使用优先队列做法(这个是我们团队的大佬写的,不敢copy过来,但是可以偷偷看一下他的代码,恕我吐槽一句他的代码风真的很小清新)
运用优先队列存储“RP”值与金币数,运用sum进行判断,优先队列的头顶元素存为最大值,这样子“ans”所得的结果就是最大值。
最后,是运用小根堆来解题,当然我并不是很清楚思路,似乎是使用堆排序,把最大值放到树的前端,然后调用来着(弱弱的我,打算溜走)
给上题目里的标程,希望对大家的理解有帮助:
#include<cstdio> #include<algorithm> using namespace std; const int N = 201013; int c[N],d[N],h[N]; int tt,n,cnt; char op[N]; bool cmph(const int i, const int j) { return c[i] > c[j]; } int main() { //freopen("dragons.in","r",stdin); //freopen("dragons.out","w",stdout); scanf("%d", &n); for (int i = 1; i <= n; ++i) scanf("%s%d", op + i, c + i); tt = 0; for (int i = 1; i < n; ++i) if (op[i] == 'e') { while (tt && c[d[tt]] >= c[i]) --tt; d[++tt] = i; } d[tt + 1] = n; tt = 0; for (int i = 1, j = 1; i < n; ++i) if (op[i] == 'c') { h[++tt] = i; push_heap(h + 1, h + tt + 1, cmph); } else if (i == d[j]) { while (tt >= c[i]) pop_heap(h + 1, h + tt-- + 1, cmph); ++j; } if (tt >= c[n]) { int ret = 0; for (int i = 1; i <= tt; ++i) ret += c[h[i]]; printf("%d\n", ret); } else puts("-1"); return 0; }
好啦,我还是总结个人的理解吧;
我的理解学习来自这几个博客主:ganggexiongqi,山代王,kiu000
堆的定义:
n个关键字序列L[1…n]称为堆,当且仅当该序列满足:
1. L(i)<=L(2i)且L(i)<=L(2i+1)
2. L(i)>=L(2i)且L(i)>=L(2i+1)
满足第一个条件的成为小根堆(即每个结点值小于它的左右孩子结点值),满足第二个添加的成为大根堆(即每个结点值大于它的左右孩子结点值)。
关于小根堆的创建:
唔,应该是类似于创建树。
1. 复制堆数组
2. 找到最初的调整位置,即找到最后一个分支结点
3.1自底向上逐步扩大形成堆
3.2 向前交换一个分支结点
小根堆的插入:
1. 将待插入元素插入已建成堆的最后面
2. 沿着出入位置所在的分支逐步向上调整
小根堆的删除:
1. 将堆顶元素删除
2. 将数组中最后一个元素放到堆顶
堆的操作:
heapify(heap,i):若节点heap[i]左子树和右子树都满足最小堆的性质,而heap[i]节点不满足最小堆性质,
即heap[i]>heap[i*2]或者heap[i]>heap[2*i+1],则操作heapify(heap,i)调整heap[i]的位置来保持堆的性质。这是堆的基本操作。
heapinsert(heap,val):往堆里面插入值val,新增节点heap[n+1]=val,并比较新增节点和其父节点大小,不断调整新增节点的位置,保持最小堆的性质。
heappop(heap):弹出堆顶元素,并令heap[0]=heap[n],堆大小减一,之后执行heapify(heap,0)来维持堆的性质。
ganggexiongqi那里有一幅图有助于理解:
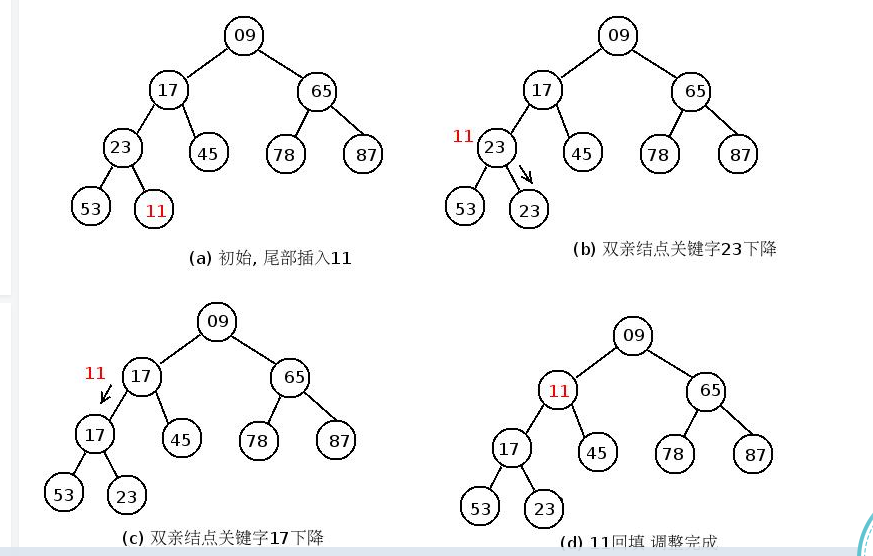
大佬代码:
public static int[] heapSort(int[] A, int n, int k) { if(A == null || A.length == 0 || n < k){ return null; } int[] heap = new int[k]; for(int i = 0; i < k; i++){ heap[i] = A[i]; } buildMinHeap(heap,k);//先建立一个小堆 for(int i = k; i < n; i++){ A[i-k] = heap[0];//难处堆顶最小元素 heap[0] = A[i]; adjust(heap,0,k); } for(int i = n-k;i < n; i++){ A[i] = heap[0]; heap[0] = heap[k-1]; adjust(heap,0,--k);//缩小调整的范围 } return A; } //建立一个小根堆 private static void buildMinHeap(int[] a, int len) { for(int i = (len-1) / 2; i >= 0; i--){ adjust(a,i,len); } } //往下调整,使得重新复合小根堆的性质 private static void adjust(int[] a, int k, int len) { int temp = a[k]; for(int i = 2 * k + 1; i < len; i = i * 2 + 1){ if(i < len - 1 && a[i+1] < a[i])//如果有右孩子结点,并且右孩子结点值小于左海子结点值 i++;//取K较小的子节点的下标 if(temp <= a[i]) break;//筛选结束,不用往下调整了 else{//需要往下调整 a[k] = a[i]; k = i;//k指向需要调整的新的结点 } } a[k] = temp;//本趟需要调整的值最终放到最后一个需要调整的结点处 }
堆排序和优先队列:
由上述堆的基本操作基本可以实现堆排序和优先队列。
堆排序:1,在线算法,不断heapinsert接受所有的数据后,heappop输出所有数据
2,离线算法,利用heapify操作创建最小堆,heappop输出所有数据
优先队列:heapinsert插入优先队列,heappop弹出优先队列

