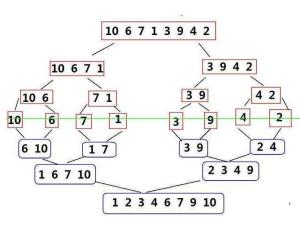
求逆序对需要用到归并排序and树状数组,这对于逆序对的查找有巨大作用。
例题:
NO.1 洛谷P1908 传送门
NO.2 洛谷P2448 乾坤大挪移
第二题更难(对,没错)
归并排序运用了二分查找思想(分治法)
具体思想如下:
如 设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11,;
逆序数为14;
如同字面意思一样,分而治之,即拆开来搜索,找到逆序对
这里,分是指二分,取一个中间数,当l=r时,二分停止,这个时候,数组内的样子就是一个一个碎片数。
这个时候,“分”,就完成了,而归并自然是要合并的
合并就是把这些碎片两两合并,且合并的过程中,比对两数的大小,进行排序
1->2->4->...
对于合并后总数为二的后方,由前面的向后比对,若最小就排序到最前方或最后方,直到最后排序完毕。
NO.1代码示例:
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int p[40005],ans=0; void merge(int a[],int l,int r) { if(l==r) return; int half=(l+r)/2; merge(a,l,half); merge(a,half+1,r); int i=l,j=half+1,q=l; while(i<=half&&j<=r) { if(a[i]>a[j]) { p[q++]=a[j++]; ans+=half-i+1; } else p[q++]=a[i++]; } while(i<=half) p[q++]=a[i++]; while(j<=r) p[q++]=a[j++]; for(i=l;i<=r;i++) a[i]=p[i]; } int main() { int n,a[40005]; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); merge(a,1,n); printf("%d",ans); return 0; }
归并排序示例代码:
1 void merge(int a[],int l,int r) 2 { 3 if(l==r) 4 return; 5 int half=(l+r)/2;//中间数 6 merge(a,l,half);//向左 7 merge(a,half+1,r);//向右 8 int i=l,j=half+1,q=l; 9 while(i<=half&&j<=r)//搜索 10 { 11 if(a[i]>a[j]) 12 { 13 p[q++]=a[j++]; 14 ans+=half-i+1; 15 } 16 else 17 p[q++]=a[i++]; 18 } 19 while(i<=half)//合并 20 p[q++]=a[i++]; 21 while(j<=r) 22 p[q++]=a[j++]; 23 for(i=l;i<=r;i++) 24 a[i]=p[i]; 25 }
然后讲讲树状数组,这里求逆序对时,树状数组需要用到离散化,离散化可以加快树状数组的运行速度
其实离散化是把数值范围变小,优化数据结构,让树状数组的运行加快(runing faster!!!)
对于离散后的序列进行一次遍历,遍历过程中就向树状数组C进行插入操作(每次插入的值为1),
这里树状数组表示的是在该元素前面但是比该元素大的元素个数,进行插入操作以后就查询。
例题中的NO.2就需要用到树状数组加离散化(当然,也可以用线段树)
在这道例题中,树状数组和线段树这些东西,其实是用来优化程序的,因为数量极大,所以需要有东西来存储
树状数组;容易扩展到高纬度的数据;
这就为大数据的题目有了明确的解决方法(好吧其实没有)
70‘ 裸的树状数组加归并排序(当然也可以使用线段树)
AC:依题意:未被操作过的数不必一一统计,因为总有一个连续区间的数跟他具有相同的性质。
于是,我们先将被操作过的点存下来离散化,然后对这些点进行交换操作。
之后几乎就是普通的逆序对,树状数组存比I小的数的个数。分别计算hash后两个值之间一段产生的逆序对和端点产生的逆序对,加到答案中。
题解代码:
#include<iostream> #include<cstdio> #include<cstring> #include<string> #include<cstdlib> #include<algorithm> #include<cmath> #include<map> #define int long long using namespace std; const int Maxn=500010; map <int,int>m; struct T //建立一个结构体 { int len; int v; int order; }a[Maxn]; int cnt; long long c[Maxn]; T aa[Maxn]; long long sum[Maxn]; long long n; int lowbit(int x) //树状数组的主要部分 { return x&(-x); } void update(int t,int value) //对数组进行更新 { int i; for(i=t;i<=cnt;i+=lowbit(i)) { c[i]+=value; } } long long getsum(int x) //必须long long否则会炸 { int i; long long temp=0; for(i=x;i>=1;i-=lowbit(i)) { temp+=c[i]; } return temp; } bool cmp(T x,T y) //交换逆序对位置 { return x.v<y.v; } main() { int k; scanf("%lld",&k); for (int i=1;i<=k;i++) { int t1,t2; scanf("%lld%lld",&t1,&t2); int t3=t2,t4=t1; if (m[t1]==0) m[t1]=t1; if (m[t2]==0) m[t2]=t2; int x1=m[t3]; int x2=m[t4]; m[t1]=x1; m[t2]=x2; n=max(n,(long long)t1); n=max(n,(long long)t2); } map<int,int>::iterator it; int last=-1; for(it=m.begin();it!=m.end();++it) { if (last!=-1 && it->first!=last+1) { cnt++; a[cnt].v=last+1; a[cnt].len=it->first-last-1; a[cnt].order=cnt; last=it->first; } cnt++; a[cnt].v=it->second; a[cnt].len=1; a[cnt].order=cnt; last=it->first; } sort(a+1,a+cnt+1,cmp); for(int i=1;i<=cnt;i++) { aa[a[i].order].v=i; aa[a[i].order].len=a[i].len; } for (int i=1;i<=cnt;i++) { sum[i]=sum[i-1]+aa[i].len; } memset(c,0,sizeof(c)); long long ans=0; for(int i=1;i<=cnt;i++) { update(aa[i].v,aa[i].len); ans+=(sum[i]-getsum(aa[i].v))*a[i].len; } printf("%lld\n",ans); }
希望各位大佬,巨佬来修改,笑