对交叉熵的理解

交叉熵损失函数（Cross Entropy）

　　一般来说，Cross Entropy损失函数常用于分类问题中，十分有效。

　　说到分类问题，与之相关的还有回归问题，简述两者区别：

　　回归问题，目标是找到最优拟合，用于预测连续值，一般以区间的形式输出，如预测价格在哪个范围、比赛可能胜利的场数等。其中，y_hat表示预测值，y表示真实值，二者差值表示损失。常见的算法是线性回归（LR）。

　　分类问题，目标是找到决策边界，用于预测离散值，分类通常是建立在回归之上，如预测根据物品的颜色、轮廓判断它是哪一种物品、某个软件是否为恶意软件等，其中的损失即通过Cross Entropy损失函数来表示，常见的分类问题有softmax等。

　　从简单的例子（图像分类任务）理解Cross Entropy损失函数：

　　1、比如有三张图片，分别是苹果、香蕉、橘子。假设现有两个模型，通过softmax方式得到对于每个预测结果的概率值：

　　模型1：

预测值	真实值	是否正确
0.3 0.3 0.4	0 0 1（苹果）	正确
0.3 0.4 0.3	0 1 0（香蕉）	正确
0.2 0.3 0.5	1 0 0（橘子）	错误

　　可见，虽然样本1和2都预测正确，但优势十分微弱，也就是不稳定，下次预测可能就会出错，而对于样本3的预测则完全错误。

　　模型2：

预测值	真实值	是否正确
0.1 0.1 0.8	0 0 1（苹果）	正确
0.1 0.8 0.1	0 1 0（香蕉）	正确
0.3 0.3 0.4	1 0 0（橘子）	错误

　　可见，样本1和2不仅预测正确而且优势十分明显，也就是很稳定，下次预测大概率预测正确，对于样本3的预测虽然错误，但不是很夸张。

　　基于这个例子，一般有如下几种损失函数：

　　1.1 Classification Error（分类错误率）

　　最简单的损失函数，计算公式为：错误的样本数 / 总样本数：

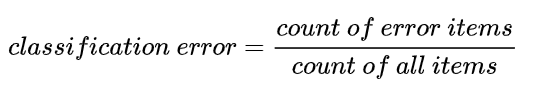
　　对于两个模型，CE都为1 / 3，因此，该方法并不能比较上面两个模型的好坏，所以一般不使用该损失函数。

　　1.2 Mean Squared Error (均方误差)

　　均方误差是比较常见的损失函数，定义为：

 

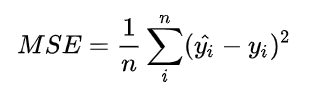
 　　y_hat为上表中的预测值，y为上表中的真实值，经计算：

　　模型1的MSE为0.69，模型2的MSE为0.29，可见，通过MSE可以判断两个模型的好坏，但弊端在于，在分类问题中，使用sofrmax得到概率，配合MSE损失函数时，采用梯度下降法（Gradient Descent）进行学习时，会出现模型一开始训练时，学习速率就非常慢的情况。

　　1.3 Cross Entropy Loss Function（交叉熵损失函数）

　　（1）二分类

　　　　在二分的情况下，模型最后的预测只有两种情况，对于这两种情况的概率为p和1-p，此时表达式为：

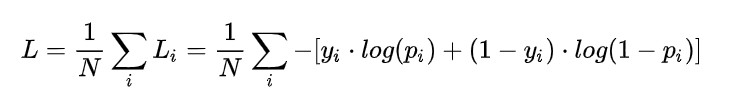　　 　　　　其中， 表示样本 i 的label，正确为 1 ，错误为 0 ；  表示样本 i 预测为正确的概率；N表示样本总数。

　　（2）多分类

 　　　　多分类就是在二分类的基础上进行扩展：

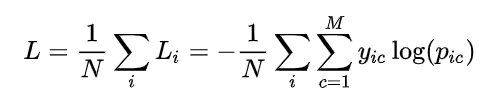
　　　　其中，M 表示类别的数量；  表示符号函数（0 或  1），如果样本 i 的真实类别等于 c 取 1 ，否则取 0； 表示观测样本 i 属于类别 c 的预测概率。

　　　　使用上述公式对所有样本的loss求平均，模型1为0.5，模型2为0.23，可以发现模型2效果更好。

 　　（3）函数性质

 

 

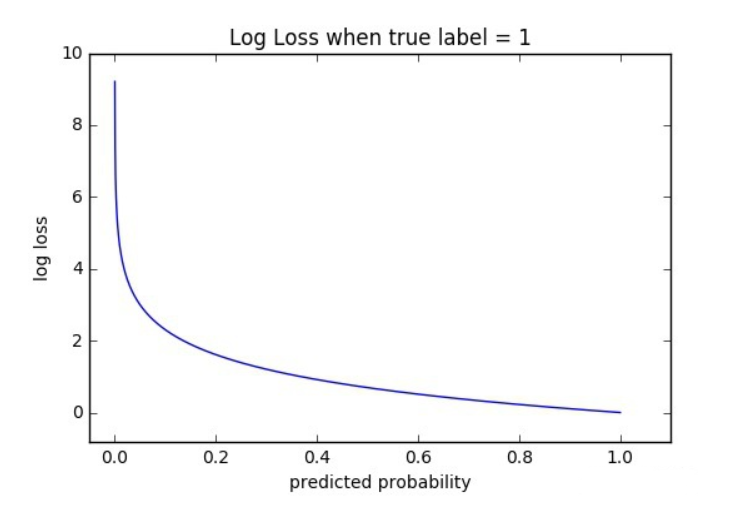
 　　　　该看出该函数是凸函数，求导时可以得到全局最优值。

　　（4）优点

　　　　在用梯度下降法（Gradient Descent）做参数更新的时候，使用逻辑函数得到概率，并结合交叉熵当损失函数，在模型效果差的时候学习速度比较快，在模型效果好的时候学习速度变慢。

　　最后，概括来说，损失函数的作用就是它找到训练集中的真实类别，然后试图使该类别相应的概率尽可能高，确保该模型表现优异。