CF 漫游(一)
CF 漫游(一)
$ 1500 - 1600 $ 分题,消磨一下时间
为了给广大尽管不存在的读者一个良好的阅读体验,我尽量缩减题解长度
CF332B
枚举第一个区间,倒序,同时维护第二个区间即可
CF997A
考虑希望把所有连续的 $ 0 $ 聚在一起,或者一个一个消掉,关键在于 $ x $ 和 $ y $ 大大小关系,所以答案是 $ \min (x, y) \times cnt + y $,这里 $ cnt $ 表示连续的 $ 0 $ 的个数
CF316E1
用线段树维护一下 $ s_0, s_1 $,表示如下:
$ s_0 = f_0 \times a_l \dots $
$ s_1 = f_1 \times a_l \dots $
然后推推式子发现 $ s_i = s_{i - 1} + s_{i - 2} = f_{i - 1} \times s_1 + f_{i - 2} \times s_0 $
合并的时候左边取 $ s_0 $,右边取 $ s_{lsize} $
打标记推式子得到:
$ f_0 \times (a_l + d) \dots = s_0 + d \times (f_0 + \dots + f_{r - 1}) $
然后就做完了
CF468A
简单构造题,如果 $ n \le 4 $,那么不可能
如果 $ n $ 是奇数,那么用前 $ 5 $ 个凑,否则用前 $ 4 $ 个凑,这样一定能剩下偶数个,然后相减乘过去就行了
CF545C
进行一下转化,把每个树转化成两个区间,然后变成了区间覆盖,可以证明,同一棵树转化成的两个区间一定不相交
CF2A
一个简单的 map 模拟题,直接做就行了,注意审题
CF1562C
一个简单的结论题,如果左半部分有 $ 0 $,那么可以把 $ 0 $ 放在开头,这样 $ k = 1 $
如果右半部分有 $ 0 $,那么把 $ 0 $ 放在末尾,这样 $ k = 2 $
否则全是 $ 1 $,可以找到两个相同的子串
做完了
CF1366C
这个比较简单,我们需要搜索,维护出第 $ i $ 步能走到的点,在题目的限制下,这些点不会重复
第 $ i $ 步和第 $ n - i + 1 $ 步能走到的点一定相同,然后记录答案即可
CF510B
简单题,深搜找环就可以了
CF1651C
考虑第一个和最后一个需要连边,所以我们只需要考虑第一个和最后一个,注意要特判他们自己连边的情况,需要保证代价最小
CF1101E
最后一道 $ 1500 $ 了
模拟
CF1632C
被某人秒了,首先如果 $ a \ge b $ 那么没法做操作 $ 3 $,直接返回答案
否则模拟即可
CF1363C
又被秒了,这是一个博弈论,如果可以直接赢就直接赢,否则判断 $ n $ 的奇偶性,手玩一下就行了
CF156B
一个简单的小题,枚举谁是罪犯,记录可能的罪犯,然后就判断每个人说的是真假话就行
CF847B
其实比较简单,考虑模拟,然后每次需要找到一个合适的位置,二分就行了
CF1213D2
这个是一个神奇的简单题,我们枚举每个数,进行操作记录,然后维护一下次数总和,然后枚举答案进行更新就可以了
CF1527C
水题一眼秒
首先考虑一对 $ (x, y) $,它的贡献是 $ x \times (n - y + 1) $
于是我们倒序枚举左端点,同时维护 $ n - y + 1 $,用 map 即可
CF518A
这是简单水题,按逆序对找下一个判断是否合法即可
CF333A
简单题,枚举面值,找到第一个不能整除的,算答案即可
CF1284C
推式子题,对于一个长度是 $ i $ 区间 $ [l, r] $,它的贡献是 $ (n - i + 1)! $
然后因为长度为 $ i $ 的区间有 $ n - i + 1 $ 个,所以再乘上一个 $ n - i + 1 $
然后因为长度为 $ i $ 的区间内部可以乱排,所以再乘上 $ i! $
最终答案是 $ \sum_{i = 1}^n (n - i + 1)! \times (n - i + 1) \times i! $
CF1526C2
一直加下去,如果加到一个数并且当前为负,把之前最小的减去即可,用堆维护
CF1537E1
找最小的前缀拼即可
CF1753B
注意到 $ (i + 1) \times i! = (i + 1)! $,所以可以向上合并,然后如果还剩下 $ a_i $ 比 $ x $ 小的,就不行,否则就行
CF525C
从大到小排序,能匹配就匹配,这样是最优的
CF643B
简单题,构造图如下即可:
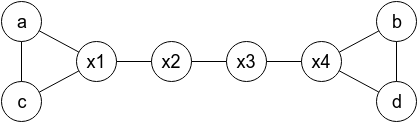
CF1633D
先预处理 $ f_i $ 表示变成 $ i $ 的最少步数,然后把步数看成代价做 $ 01 $ 背包即可


