可持久化数据结构学习笔记

可持久化数据结构学习笔记

简介

可持久化就存储历史版本

基础部分

可持久化线段树的用途是，对于一个区间操作，我们可能只需要考虑一个区间内的东西，但是如果使用普通的线段树有难以解决，所以会用到

具体来说，每次插入一个点，我们就要新建一颗线段树，作为一个版本，这样考虑区间只需要类似前缀和的思想即可

但是这样又非常浪费空间，所以我们可以只考虑存储改变了的点，其他的直接一个指针指过去，这就是可持久化线段树的基本思想

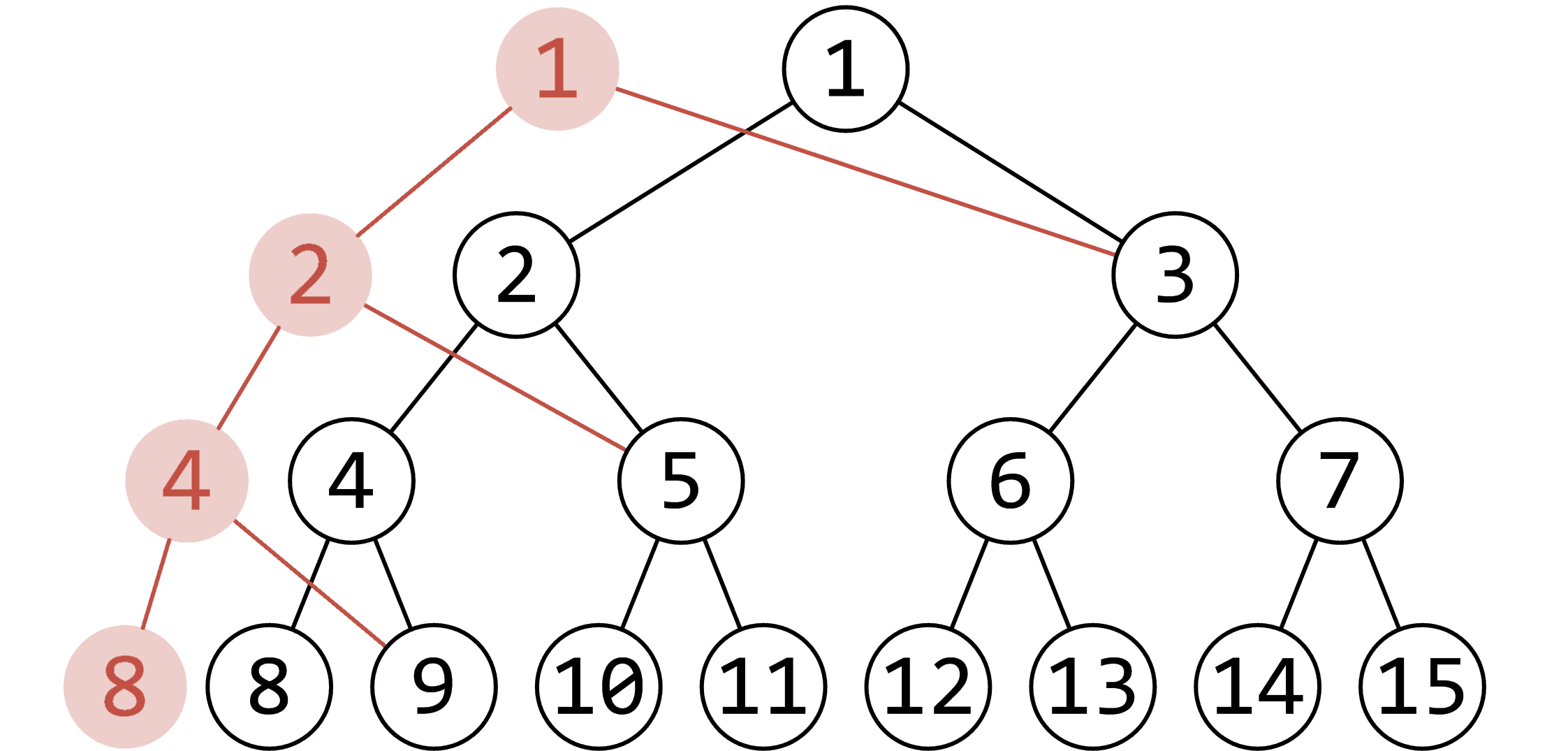
例如这个图，我们就可以看出来，我们只需要存储 $ 1, 2, 4, 8 $，其他的点用指针指到上一个版本指的点即可

代码可以这样写：

const int N = 200005;

int n, a[N], b[N], len, tot;

int L[N << 5], R[N << 5], sum[N << 5], root[N];

inline int get (int val) {

    return lower_bound (b + 1, b + 1 + len, val) - b;

}

inline int build (int l, int r) {

    int rt = ++ tot;

    if (l == r) return rt;

    int mid = (l + r) / 2;

    L[rt] = build (l, mid), R[rt] = build (mid + 1, r);

    return rt;

}

inline int update (int rot, int l, int r, int k) {

    int rt = ++ tot;

    L[rt] = L[rot], R[rt] = L[rot], sum[rt] = sum[rot] + 1;

    if (l == r) return rt;

    int mid = (l + r) / 2;

    if (k <= mid) L[rot] = update (L[rot], l, mid, k);

    else R[rot] = update (R[rot], mid + 1, r, k);

    return rt;

}

inline int query (int u, int v, int l, int r, int k) {

    int mid = (l + r) / 2, x = sum[L[v]] - sum[L[u]];

    if (l == r) return l;

    if (k <= x) return query (u, v, l, mid, k);

    else return query (u, v, mid + 1, r, k - x);

}

inline void init () {

    for (int i = 1; i <= n; ++ i) b[i] = a[i];

    sort (b + 1, b + 1 + n);

    len = unique (b + 1, b + 1 + n) - b - 1;

    root[0] = build (1, len);

    for (int i = 1; i <= n; ++ i) root[i] = update (root[i - 1], 1, len, get (a[i]));

}

inline void solve (int l, int r, int k) {

    return b[query (root[l - 1], root[r], 1, len, k)];

}