杨辉三角的秘密
杨辉三角的秘密
杨辉三角的构建
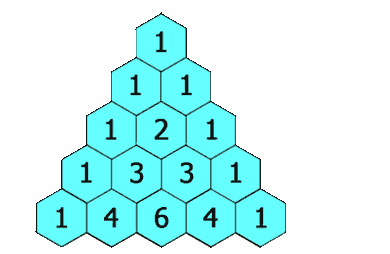
我们可以简单的注意到,每个数字都是他上面两边的数字之和,也就是说,在两肩的位置
然后我们就构造出了杨辉三角,我们看一张动图加深理解:
秘密一:隐藏的数列
首先我们把杨辉三角左对齐,得到:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
第一列都是 $ 1 $,第二列是从 $ 1 $ 开始的自然数,第三列的话看这里:
可以看到,第三列就是三角数
第四列是构成四面体所需要的点的数目,四面体就是由一堆三角形摞起来的:
在几何上,单纯形是某一维度空间中构造最简单的结构,$ 0- $ 单纯形就是点,$ 1- $ 单纯形就是一条线段,$ 2- $ 单纯形就是三角形,$ 3- $ 单纯形就是四面体,$ 4- $ 单纯形就是五胞体。
然后下面是所有的隐藏数列及其规律:
秘密二:$ 2 $ 的幂
如果我们把杨辉三角的第 $ i $ 行所有的数相加,然后我们就可以看出来,它们的和就是 $ 2^{i - 1} $
秘密三:$ 11 $ 的幂
这里我们会发现,如果把第 $ i $ 行的所有数拼起来,就可以得到 $ 11^{i - 1} $
我们考虑到两位数的情况,这里两位数的话我们考虑进位,就像这样:
秘密四:完全平方数
这里我们可以发现,第二列的数的平方是它右边和右下数的和
秘密五:斐波那契数列
这里我们把对角线的数全部加起来,就可以得到斐波那契数列,是不是非常神奇
秘密六:谢尔宾斯基三角
这里我们把杨辉三角里面所有的奇数用红色标出来,你发现了什么
没错,就是谢尔宾斯基三角
这是一个美妙的性质
秘密七:组合数
这里我们可以发现,杨辉三角形是和组合数有着密切联系的:
然后我们就可以使用肉眼观察到:$ C(n, m) -= C[n + 1][m + 1] $
这里 $ C[i][j] $ 表示杨辉三角第 $ i $ 行第 $ j $ 列
秘密八:二项式的展开
二项式指的是 $ (x + y)^k $ 的形式的式子
我们举例子即可
当 $ k = 2 $ 时,$ (x + y)^2 = x^2 + 2xy + y^2 $
然后我们再看 $ k = 3 $ 的情况,$ (x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3 $
然后我们就找到了规律:
秘密九:二项式定理
这里我们可以根据以下证明推出公式
首先我们枚举每一个项,如果这个项长这样:$ x^n y^m $,那么一定有 $ n + m = k $
所以我们考虑这个项出现的次数就是 $ C(k, n) $,然后这个项就是 $ C(k, n)x^n y^m $
每个项都长这样,所以我们直接的出公式:
秘密十:二项式分布
二项式分布描述了具有两种可能结果的实验的概率分布。事实上,杨辉三角的每一行也能揭示了这样的清晰,最经典就是扔一枚硬币为例
如果考虑抛 $ 3 $ 次硬币,就会有 $ 8 $ 种可能发生的事件:
反反反 反反正 反正反 反正正
正反反 正反正 正正反 正正正
可以分为 $ 4 $ 类情况:
- $ 3 $ 次反面 —— 只有 $ 1 $ 次发生
- $ 2 $ 次正面和 1 次反面 —— 有 $ 3 $ 次发生
- $ 2 $ 次反面和 1 次正面 —— 有 $ 3 $ 次发生
- $ 3 $ 次正面 —— 只有 $ 1 $ 次发生
这里的 $ 1,3,3,1 $ 也就是杨辉三角的第 $ 4 $ 行
这里我们设抛硬币抛到正面的概率是 $ p $,那么公式如下:
这个和二项式定理的公式非常像,只不过这没有求和


