题解 CF760B
题解 CF760B
考虑二分 \(k\) 位置的枕头个数 \(x\) ,因为相邻的位置枕头个数与当前位置个数差不能大于 \(1\) ,所以考虑通过当前位置枕头个数来求出 \(n\) 个位置上枕头个数的总和,可以考虑分为 \([1,i),[i,k),[k,j),(j,n]\) 四个区间,其中第一个和最后一个区间为每个位置枕头数都为 \(1\) 的区间,第二个区间的值域为 \([1,x)\) 第三个区间的值域为 \([x,1]\) 。
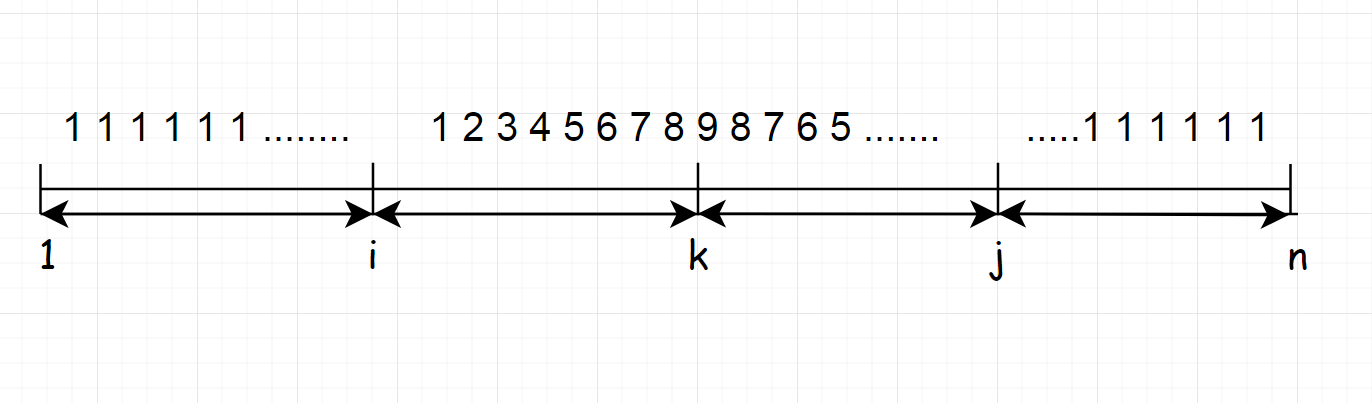
因为第二三个区间如图规律,所以很容易得出:第二个区间长度为 \(len=x-1\) ,第三个区间长度为 \(ren=x\) 。
!! 若第二三个区间不完整,则没有第一四个区间,二三区间长度分别为 \(\min(len,k-1),\min(n-k+1,ren)\) 。
考虑怎么统计:
- 第一个区间总和很明显为 \(k-1-len\) 。
- 第四个区间总和为 \(n-(k+ren-1)\) 。
- 第二个区间和为
\[(x-1)+(x-2)+\dots +(x-len)
\]
\[\sum_{1}^{len}x-1-2-\dots -len
\]
\[\sum_{1}^{len}x-(1+2+\dots +len)
\]
\[\sum_{1}^{len}x-\frac{len\times(1+len)}{2}
\]
\[len\times x-\frac{len+len^2}{2}
\]
- 第三个区间和为
\[x+(x-1)+(x-2)+\dots+(x-(ren-1))
\]
\[\sum_{1}^{ren}x-0-1-2-\dots -(ren-1)
\]
\[\sum_{1}^{ren}x-(0+1+2+\dots +(ren-1))
\]
\[\sum_{1}^{ren}x-\frac{ren\times(0+ren-1)}{2}
\]
\[ren\times x-\frac{ren^2-ren}{2}
\]
以上所有总和为当 \(k\) 位置有 \(x\) 个枕头时,总的枕头数,若大于给定 \(m\) ,则需要调小数值,小于则反之。
#include<cstdio>
#include<vector>
#include<cstring>
#define int long long
using namespace std;
template<typename T>T read(T &x){char c=getchar();x=0;T f=1;for(;c<'0' || c>'9';c=getchar())if(c=='-') f=~f+1;for(;c>='0' &&c<='9';c=getchar()) x=(x<<3)+(x<<1)+(c^'0');return x=x*f;}
template<typename T,typename...T2>void read(T &x,T2 &...y){read(x);read(y...);return;}
int n,m,k;
bool check(int x){
int len=x-1,ren=x;
len=min(len,k-1),ren=min(ren,n-k+1);
int sum=x*len-(len+len*len)/2+k-len-1+ren*x-(ren*ren-ren)/2+n-(k+ren-1);
if(sum>m) return 0;
return 1;
}
signed main(){
read(n,m,k);
int l=1,r=m+1;
while(l<r){
int mid=(l+r)>>1;
if(check(mid)) l=mid+1;
else r=mid;
}
printf("%lld",l-1);
return 0;
}


