题解 P8865 [NOIP2022] 种花

题解 P8865

鄙人没能去NOIP，赛后看的T1

此题按照题目思路一步一步进行模拟，最后思维优化一下，即可拿到 100 分的好成绩。

\(n^3\)的暴力大家肯定都会打，这里就不加以赘述了，看本题题解其他大佬的题解相信也可以理解。

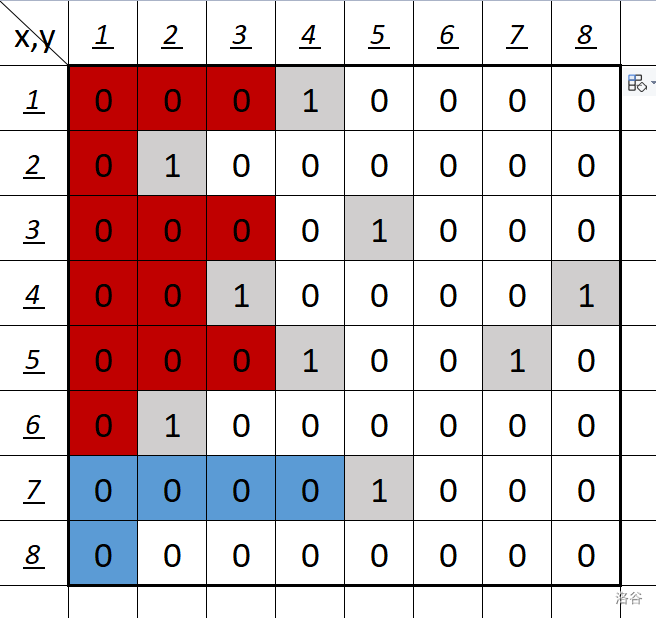
（坑为 1 ，非坑为 0 ，图中的颜色稍后会进行解释。）

我们首先考虑如何进行优化，我们会发现，

如果条件满足 C 形，或者是 F 形，\(x_1,x_2\) 行上所有的 0 一定会对答案进行贡献，所以我们考虑记录在 a[i][j] 位置向右连续的 0 数量（因为C 和 F 横着的部分都向右）。

memset(r,0ll,sizeof(r));
for(int i=1;i<=n;i++){
    for(int j=m;j>=1;j--){
        r[i][j]=a[i][j]==1?0:r[i][j+1]+1;
    }
}

因为图形 F 在 \(x_2\) 位置以下到 \(x_3\) 的位置还会有连续的 0 ，所以我们要考虑这一部分应该如何优化。

举个例子，比如对于图中 \(x_1=1,x_2=3,y_0=1\) 的情况，我们会发现， \(x_2=3\) 及以下的 6 个 0 都会对 F 的答案进行贡献，所以我们要记录 a[i][j] 及以下，连续的 0 的个数。

memset(d,0ll,sizeof(d));
for(int j=1;j<=m;j++){
    for(int i=n;i>=1;i--){
        d[i][j]=a[i][j]==1?0:d[i+1][j]+1;
    }
}

所有的初始化已经写好了，接下来考虑如何进行计算答案。

如果我们枚举 \(x_2\) 以及 \(y_0\) ，我们就可以通过刚刚初始化好的 r[],d[] 数组找到 \(x_3\) 以及 \(y_2\) ，但是如果想要计算最终的答案，我们还要找到 \(x_1\) 和 \(y_1\) ，因为找到 \(x_1\) 也就可以找到对应的 \(y_1\) ，所以我们只需要思考如何找到 \(x_1\) 即可。

我们并没有初始化此部分，所以我们可以考虑在最终计算答案的时候记录下来。

看图，当我们枚举到 \(x_2=7,y_0=1\) 时，我们会发现，以上所有的行上的贡献都会加到此位置上，也就是说，我们需要记录下来，到位置 \(x_2\) 时，上面已经有多少贡献加到了此位置上，这个贡献稍微思考一下就会发现只有每一行的贡献加到了此处，所以我们在枚举的时候，可以将每一行的贡献（也就是 r[i][j]) 加入一个变量 sum ，计算时行上的贡献直接由 sum 计入即可。

这里如果中间的连续 0 断开的话， sum 就应该清零。

int sum=0ll,C=0ll,F=0ll;
for(int j=1;j<=m;j++){
    for(int i=3;i<=n;i++){
        if(a[i][j]){
            sum=0ll;
            i+=2ll;
            continue ;
        }
        if(!a[i-1][j]){
            if(r[i-2][j]>=1){
                sum+=r[i-2][j]-1;
            }
        }
        C=(C+sum*max(0ll,r[i][j]-1)%p)%p;
        F=(F+sum*max(0ll,r[i][j]-1)*max(0ll,d[i][j]-1)%p)%p;
    }
    sum=0ll;
}

最终代码

// #Tyrue#
#include<map>
#include<cmath>
#include<cstdio>
#include<string>
#include<iostream>
#include<string.h>
#include<algorithm>
#define int long long
using namespace std;
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9')
        x=x*10+ch-'0',ch=getchar();
    return x*f;
}
const int N=1e3+10,p=998244353;
int T,n,m,c,f;
int a[N][N],r[N][N],d[N][N];
signed main(){
    T=read(),n=read();
    while(T--){
        n=read(),m=read(),c=read(),f=read();
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                scanf("%1lld",&a[i][j]);
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=m;j>=1;j--){
                r[i][j]=a[i][j]==1?0:r[i][j+1]+1;
            }
        }
        for(int j=1;j<=m;j++){
            for(int i=n;i>=1;i--){
                d[i][j]=a[i][j]==1?0:d[i+1][j]+1;
            }
        }
        int sum=0ll,C=0ll,F=0ll;
        for(int j=1;j<=m;j++){
            for(int i=3;i<=n;i++){
                if(a[i][j]){
                    sum=0ll;
                    i+=2ll;
                    continue ;
                }
                if(!a[i-1][j]){
                    if(r[i-2][j]>=1){
                        sum+=r[i-2][j]-1;
                    }
                }
                C=(C+sum*max(0ll,r[i][j]-1)%p)%p;
                F=(F+sum*max(0ll,r[i][j]-1)*max(0ll,d[i][j]-1)%p)%p;
            }
            sum=0ll;
        }
        memset(r,0ll,sizeof(r));
        memset(d,0ll,sizeof(d));
        printf("%lld %lld\n",c*C,f*F);
    }
    return 0;
}