题解 CF1713A

题解 CF1713A

这个题其实并不难

因为要便利所有的点并且左右的点都是在坐标系轴上

并且这里的移动只能是上下左右水平移动

所以我们最后走出来的图形，一定是个多边形

然后让我们看一下这张图片

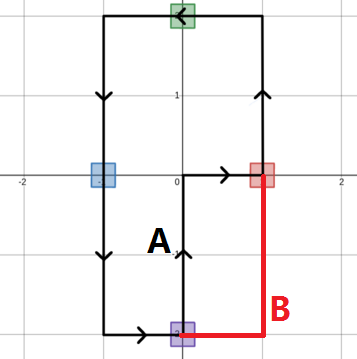
我们会发现，这里走 A 路径，和走 B 路径所用的步数是完全相同的

所以，最终走出来的这个路径一定是一个规整的矩阵

我们观察一下，就会发现，这个矩阵的周长会受 4 个点的影响

分别是 \(X_{max}\) , \(Y_{max}\) , \(X_{min}\) , \(Y_{min}\)

所以，我们只需要在读入的时候将这四个点处理出来，就行了

这里有一点需要注意，因为最终要回到原点，所以，我们的转化前的路径一定是要经过 \((0,0)\) 这个点的

所以，我们的 \(X_{max}\) , \(Y_{max}\) , \(X_{min}\) , \(Y_{min}\) 在初始化时，应该都设为 0 这样才能保证他的点在一边时，可以回到原点

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstring>
#include<stack>
#include<map>
#define Max(x,y) x>y?x:y
#define Min(x,y) x<y?x:y
using namespace std;
int T; 
int main(){
	scanf("%d",&T);
	while(T--){
		int n,fx,fy,maxn_x=0,maxn_y=0,minn_x=0,minn_y=0;
		scanf("%d",&n);
		for(int i=1;i<=n;i++){
			scanf("%d %d",&fx,&fy);
			maxn_x=Max(maxn_x,fx);
			maxn_y=Max(maxn_y,fy);
			minn_x=Min(minn_x,fx);
			minn_y=Min(minn_y,fy);
		}
//		printf("%d %d %d %d",maxn_x,maxn_y,minn_x,minn_y);
		printf("%d\n",(maxn_x-minn_x+maxn_y-minn_y)*2);
	}
    return 0;
}