题解 CF1711B

题解 CF1711B

这个题说明了，蛋糕的个数只跟好友的对数有关，跟去的人或者是单个的人的个数是无关的（是不是单个的人去没有蛋糕吃）

所以我们就要考虑，怎样才能满足吃掉的蛋糕正好是偶数

我们会发现，这个吃掉的蛋糕数会一定程度跟 m 有关

• 如果 m 是偶数，那我们就不需要去掉几个人，直接就可以满足条件
• 如果是奇数，我们就要考虑删掉几个人，这里想一下就会发现，我们删掉一个人或者是删掉两个人一定是可以让删后的对数为偶数的，并且是最优的

所以，现在问题就是如何去选择删哪个或哪些人

• 如果删掉一个人，因为要保证删完对数为偶数，所以我们删掉的人肯定必须要存在于奇数个对中（偶数-奇数=奇数），从这里面去取最小值

• 如果删掉两个人，我们也要保证删完之后对数为偶数，所以我们要想怎样删完之后才能使偶数呢？

  也就是这两个人必须是一对的，如果不是一对的，那我们只能考虑删掉一个人存在于奇数个和一个人存在于偶数个，这样显然不如直接选一个人存在于奇数个优，所以我们就要考虑这两个人存在于偶数对数之中，也就是之前没有出现过的情况，为了保证删完为偶数，所以这两个人必须是一对的，也就是这两个点之间有边，并且保证他们相加的度数为偶数

  看图

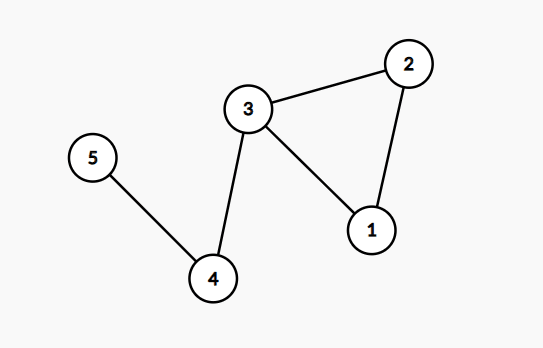
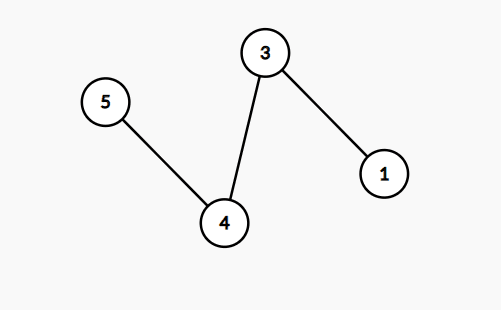
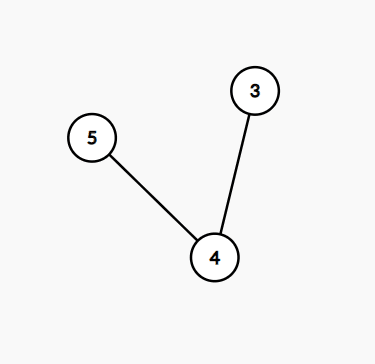
这里选择删掉 2 和 1 ，满足最终的对数为偶数（图3），如果只删 2 会导致，还是为奇数（图2）

// #Tyrue#
#include<map>
#include<cstdio>
#include<string>
#include<iostream>
using namespace std;
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9')
        x=x*10+ch-'0',ch=getchar();
    return x*f;
}
const int N=1e5+10;
int T,n,m;
int a[N],du[N];
struct Node{
    int x,y;
}edge[N];
int main(){
    T=read();
    while(T--){
        n=read(),m=read();
        for(int i=1;i<=n;i++){
            a[i]=read();
            du[i]=0;
        }
        for(int i=1;i<=m;i++){
            edge[i].x=read(),edge[i].y=read();
            du[edge[i].x]++;
            du[edge[i].y]++;
        }
        if(m%2==0){
            puts("0");
        }else{
            int minn=1e9;
            for(int i=1;i<=m;i++){
                // if(!((du[edge[i].x]+du[edge[i].y])&1)){
                if(du[edge[i].x]&1){
                    minn=min(minn,a[edge[i].x]);
                }
                if(du[edge[i].y]&1){
                    minn=min(minn,a[edge[i].y]);
                }
                if((du[edge[i].x]+du[edge[i].y])%2==0){    
                    minn=min(minn,a[edge[i].x]+a[edge[i].y]);
                }
            }
            printf("%d\n",minn);
        }        
    }
    return 0;
}