HL 7.19 FFT多项式乘法

前几天写的FFT，写一下自己的理解；

最近很不爽 生病了 还被踩 吊着锤；

FFT就是快速解决多项式乘法的问题，闵神讲的课还是比较好的，至少我差不多都听懂了；

由于我们知道n次多项式可以由n个点唯一确定，那么我们可以将n次多项式的单位根0-n-1带入，但是这样仍然是O(n^2)的；

前置芝士：复数，欧拉公式，单位根，基本运算水平；

我们设多项式A(x)的系数为(a0,a1,a2,…,an−1)

那么A(x)=a0+a1∗x+a2∗x2+a3∗x3+a4∗x4+a5∗x5+⋯+an−2∗xn−2+an−1∗xn−1

将其下标按照奇偶性分类

A(x)=(a0+a2∗x2+a4∗x4+⋯+an−2∗xn−2)+(a1∗x+a3∗x3+a5∗x5+⋯+an−1∗xn−1)

设A1(x)=a0+a2∗x+a4∗x2+⋯+an−2∗xn2−1

A2(x)=a1+a3∗x+a5∗x2+⋯+an−1∗xn2−1

那么A(x)=A1(x2)+xA2(x2)

 

不难发现 这个式子只有常数项不同，那么我们发现其实可以将其分治做下去，一直按照下标奇偶分类，递归的去作就好；

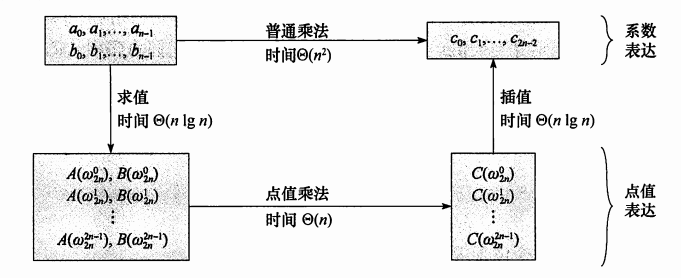
我们记录一个多项式一般是记录其系数的值，而FFT就是把系数表示变成点置表示在变成系数表示；

我们可以推导出来一个式子，系数其实最后是需要除n的，这样是代码最后一行那样写的原因；

Ck=na_k；

这就是点值和系数之间的关系，反正我是把所有式子推导了一遍，发现不是特别难，所以建议不懂得时候手算一下；

设出来一组向量，然后表示他和系数之间的关系即可；

理清一下思路；

我们用系数表示多项式，但是求值的时候有点麻烦；

我们考虑用点值表示这个多项式，但是我们最后仍需要系数表示，

我们尝试去寻找两者关系，最后发现可以分治，所以递归，所以相当于

系数到点值到系数；

偷来的图：

而且写代码的时候建议手写一下复数的运算，尽管c++自带有，但是也就几行，为了不被卡常；

当然递归版本的FFT又是会被卡掉；

其中是有一些小优化的，比如蝴蝶操作，小trick，就是主函数里注释的东西，但是我只写了递归版本（小声）所以就先不整理了；

#include<iomanip>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<queue>
#include<deque>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<stack>
#include<algorithm>
#include<vector>
#include<cctype>
#include<utility>
#include<set>
#include<bitset>
#include<map>
using namespace std;
const int N=2100010;
const double pi=acos(-1.0);
struct complex{
    double r,v;
    complex(double a=0,double b=0):r(a),v(b){}
    inline complex operator+(const complex& b){return complex(r+b.r,v+b.v);}
    inline complex operator-(const complex& b){return complex(r-b.r,v-b.v);}
    inline complex operator*(const complex& b){return complex(r*b.r-v*b.v,v*b.r+r*b.v);}
};
inline void swap(complex& a,complex& b){complex t(a);a=b;b=t;}
int n,m,L,H;
complex a[N],b[N],temp[N];
complex w[N];

void FFT(complex* a,int len,int f){
    if(len==1)return;
    for(int i=0;i<len/2;i++)
        temp[i]=a[i*2],temp[i+len/2]=a[i*2+1];
    for(int i=0;i<len;i++)
        a[i]=temp[i];
    FFT(a,len/2,f),FFT(a+len/2,len/2,f);
    complex wn(cos(2*pi/len),f*sin(2*pi/len)),w(1,0);
    for(int i=0;i<len/2;i++){
        complex x=a[i],y=w*a[i+len/2];
        a[i]=x+y,a[i+len/2]=x-y;
        w=w*wn;
    }
}

int main(){
//    freopen("a.in","r",stdin);
//    freopen("a.out","w",stdout);
    ios::sync_with_stdio(false);
    w[0].r=1;
    cin>>n>>m;
    n++; m++;
    for(int i=0;i<n;i++) cin>>a[i].r;
    for(int i=0;i<m;i++) cin>>b[i].r;
    for(L=1,H=0;L<(n+m-1);H++) L<<=1;
//    for(int i=0;i<L;i++)
//        R[i]=(R[i<<1]<<1)|((1&i)<<(H-1));
    FFT(a,L,1); FFT(b,L,1);
    for(int i=0;i<L;i++)
        a[i]=a[i]*b[i];
    FFT(a,L,-1);
    for(int i=0;i<n+m-1;i++) cout<<(int)(a[i].r/L+0.5)<<' ';
    return 0;
}

以上是我对FFT的浅陋理解，可能会有错误，但是写代码的时候和Chdy大佬也是争执了很多不同的看法，可能以后才会补坑吧；

洛谷的这个模板题解还是不错的，推荐；