HL 7.14 整理杂题 随笔
浑浑噩噩在HL过了九天,整理点杂题,因为课程安排很紧,然后一些题没有来的及写,所以整理下思路,整理一些写的水题;
每天的课程很有意思,因为听不懂,这两天初等数论就数学偏多一点,所以就有点头大;
此题展现我垃圾的反演水平,昨天被反演晕了,我也是头次尝试自己搞一些一堆sigma在一起的神仙东西,昨天搞懂这些东西;
不过我承认,我的反演限于没有入门;
这个博客园的数学公式编译怎么搞,不太会,只能搞图片了;
首先 有一个公式
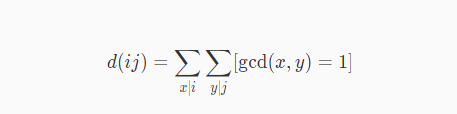
我们将其带入原始公式;
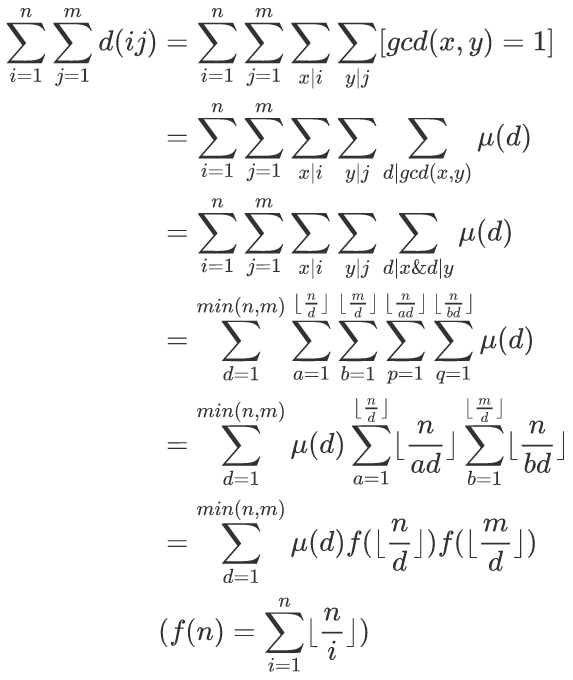
这里的u函数我们可以预处理出来并求出前缀和,对于f数组我们也可以求出,那么对于查询就可以直接带入公式;
对于u函数,ppt抠图,代码中会体现;

妙啊;反正我当时是一头蒙,不过这个题我们还有其他反演方式,这里不介绍了;对于那个公式的证明,是我在洛谷上抠的图,具体证明,有一个源神给出的,不过不在讲;

#include<bits/stdc++.h> using namespace std; const int N=50010; typedef long long ll; template<typename T>inline void read(T &x) { x=0; register int f=1; register char ch=getchar(); while (!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar(); x*=f; } ll mu[N],prime[N],check[N],sum[N],f[N]; int n=50000,tot,last,T,a,b; ll cal(int a , int b) { int last; ll ans=0; for(int i=1;i<=a&&i<=b;i=last+1) last=min(a/(a/i),b/(b/i)),ans+=(ll)(sum[last]-sum[i-1])*f[a/i]*f[b/i]; return ans; } int main() { // freopen("a.in","r",stdin); // freopen("a.out","w",stdout); mu[1]=1;sum[1]=1; //check[1]=1; for(int i=2;i<=n;i++) { if(!check[i]) mu[i]=-1,prime[++tot]=i; for(int j=1;j<=tot&&i*prime[j]<=n;j++) { check[i*prime[j]]=1; if(i%prime[j]==0) { mu[i*prime[j]]=0; break; } else mu[i*prime[j]]=-mu[i];//处理出mu } sum[i]=sum[i-1]+mu[i];//预处理前缀和; } for(int i=1;i<=n;i++) { for(int j=1;j<=i;j=last+1) { last=i/(i/j); f[i]+=(last-j+1)*(i/j); } } read(T); while(T--) { read(a); read(b); printf("%lld\n",cal(a,b)); } return 0; }
分块找区间众数,我终于填坑了,舒服;
不过我不开O2的代码能T好几组,vector的大常数;
我这里用的是二分查找+vector,我们将数字离散化之后,
在预处理时,我们只保存一段边界为端点的区间[L,R]的众数,对于查询,不完整的块;
[l,L)和(R,r]时,我们扫描其中每一个数x,我们二分查找在[l,r]中x出现多少次,第一个>=l的数,和最后一个小于等于r的数,两个下标相减在+1就是出现次数;

// luogu-judger-enable-o2 #include<bits/stdc++.h> #define mod 10007 #define inf 0x7fffffff #define ll long long using namespace std; ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n,m,blo,id; int v[50005],bl[50005]; int f[505][505]; map<int,int>mp; int val[50005],cnt[50005]; vector<int>ve[50005]; void pre(int x) { memset(cnt,0,sizeof(cnt)); int mx=0,ans=0; for(int i=(x-1)*blo+1;i<=n;i++) { cnt[v[i]]++; int t=bl[i]; if(cnt[v[i]]>mx||(cnt[v[i]]==mx&&val[v[i]]<val[ans])) ans=v[i],mx=cnt[v[i]]; f[x][t]=ans; } } int query(int l,int r,int x) { int t=upper_bound(ve[x].begin(),ve[x].end(),r)-lower_bound(ve[x].begin(),ve[x].end(),l); return t; } int query(int a,int b) { int ans,mx; ans=f[bl[a]+1][bl[b]-1]; mx=query(a,b,ans); for(int i=a;i<=min(bl[a]*blo,b);i++) { int t=query(a,b,v[i]); if(t>mx||(t==mx&&val[v[i]]<val[ans])) ans=v[i],mx=t; } if(bl[a]!=bl[b]) for(int i=(bl[b]-1)*blo+1;i<=b;i++) { int t=query(a,b,v[i]); if(t>mx||(t==mx&&val[v[i]]<val[ans]))ans=v[i],mx=t; } return ans; } int main() { n=read();m=read(); blo=200; int ans=0; for(int i=1;i<=n;i++) { v[i]=read(); if(!mp[v[i]]) { mp[v[i]]=++id; val[id]=v[i]; } v[i]=mp[v[i]]; ve[v[i]].push_back(i); } for(int i=1;i<=n;i++)bl[i]=(i-1)/blo+1; for(int i=1;i<=bl[n];i++)pre(i); for(int i=1;i<=m;i++) { int a=read(),b=read(); a=(a+ans-1)%n+1;b=(b+ans-1)%n+1; if(a>b)swap(a,b); ans=val[query(a,b)]; printf("%d\n",ans); } return 0; }
闲来无聊,写了一道博弈论的题,实际上我对博弈论并不是很熟悉,因为没有系统学过,回去再看看书吧;
不过这是个经典题目呢;
首先,合并次数为奇数先手必胜,偶数后手必胜,那么两个人都会尽可能向着自己想要的方向去发展(即拉到总合并次数为奇数/偶数);
那么我们发现如果每个人按照博弈的思路去选石子(其实原来我写的是贪心,但Chdy大佬指出来我的错误,
对于博弈是存在必胜和必败的,并不是仅仅贪心,我们要最优规划,找到必败和必胜的条件);
那么最终局面一定是这样的;
m,m,m....(共n/m个堆),n%m;
那么对于合并次数,我们也能直接求出来;
sum=(n/m)*(m-1)+n%m-1;要特判(n%m==0)的情况;
直接看%2的情况就好了;
其实还有一种思路;
每次合并我们只会使堆得数量减小1,最后会剩n/m块,判断一下n%m是否为0,如果不为0,就再添一块,是0就没有这一块;用原来的总堆数减去就好;

#include<bits/stdc++.h> using namespace std; template<typename T>inline void read(T &x) { x=0; register int f=1; register char ch=getchar(); while (!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar(); x*=f; } int T,n,m,sum; int main() { // freopen("a.in","r",stdin); // freopen("a.out","w",stdout); read(T); while(T--) { read(n); read(m); int sum=0; // sum=n-(n/m+(n%m)); sum=(n/m)*(m-1)+(n%m==0?0:n%m-1); if(sum%2==0) printf("1\n"); else printf("0\n"); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号