算法进阶 搜索 题目整理1
我终于开始写搜索了,毒瘤搜索,玄学剪枝,这东西好玄学,我感觉这些题目是很经典,但我目前还不能总结出搜索的技巧,有点头大;
但今天整理几道搜索的题目;
1.可达性统计
题目大意:给定一张N个点M条边的有向无环图,分别统计从每个点出发能够到达的点的数量。
这是一个有向无环图,我们可以想到拓扑排序来实现遍历;
从x出发,x所能到达的点,记为f(x),是它自身和它的各个后继节点所能到达的点;
而在使用拓扑序列是,对于任意的边(x,y),x均排在y之前;
在状态压缩中,我们使用一个N为二进制数,那么这里我们也可以这样考虑,对于一个f(x) ,我们使用一个N位二进制数,第i位为0则不能到达,为1则能到达;
,进行合并时,相当于按位与;最后f(x)中1的个数就是最终的答案;
而c++中的bitsit为我们提供了便捷的操作;
以下转自:https://oi-wiki.org/ds/stl/bitset/
介绍¶
std :: bitset 是标准库中的一个固定大小序列,其储存的数据只包含 0/1
众所周知,由于内存地址是按字节即 byte 寻址,而非比特 bit ,
我们一个 bool 类型的变量,虽然只能表示 0/1 , 但是也占了 1byte 的内存
bitset 就是通过固定的优化,使得一个字节的八个比特能分别储存 8 位的 0/1
对于一个 4 字节的 int 变量,在只存 0/1 的意义下, bitset 占用空间只是其
在某些情况下通过 bitset 可以使你的复杂度除以 32
当然, vector 的一个特化 vector<bool> 的储存方式同 bitset 一样,区别在于其支持动态开空间,
bitset 则和我们一般的静态数组一样,是在编译时就开好了的。
那么为什么要用 bitset 而非 vector<bool> ?
通过以下的介绍,你可以更加详细的看到 bitset 具备的方便操作
#include <bitset> // 包含 bitset 的头文件
运算符¶
operator[] : 访问其特定的一位
operator ==/!= : 比较两个 bitset 内容是否完全一样
operator &=/|=/^=/~ : 进行按位与/或/异或/取反操作
operator <</>>/<<=/>>= : 进行二进制左移/右移
operator <</>> : 流运算符,这意味着你可以通过 cin/cout 进行输入输出
vector<bool> 只具有前两项
成员函数
test() : 它和 vector 中的 at() 的作用是一样的,和 [] 运算符的区别就是越界检查
count() : 返回 true 的数量
set() : 将整个 bitset 设置成 true , 你也可以传入参数使其设置成你的参数
reset() : 将整个 bitset 设置成 false
flip() : 翻转该位 (0 变 1,1 变 0), 相当于逻辑非/异或 1
to_string() : 返回转换成的字符串表达
to_ulong() : 返回转换成的 unsigned long 表达 ( long 在 NT 及 32 位 POSIX 系统下与 int 一样,在 64 位 POSIX 下与 long long 一样)
to_ullong() C++11, 返回转换成的 unsigned long long 表达
这些 vector<bool> 基本都没有
作用
一般来讲,我们可以用 bitset 优化一些可行性 DP, 或者线筛素数 ( notprime 这种 bool 数组可以用 bitset 开到 之类的)
它最主要的作用还是压掉了内存带来的时间优化, 的常数优化已经可以是复杂度级别的优化了,比如一个 的 算法, 显然很卡,在常数大一点的情况下必然卡不过去,O(松)不能算!, 这时候如果我们某一维除以 32, 则可以比较保险的过了这道题
其实 bitset 不光是一个容器,更是一种思想,我们可以通过手写的方式,来把 long long 什么的压成每 bit 表示一个信息,用 STL 的原因更多是因为它的运算符方便

#include<bits/stdc++.h> using namespace std; #define N 30010 template<typename T>inline void read(T &x) { x=0;T f=1,ch=getchar(); while(!isdigit(ch)) ch=getchar(); if(ch=='-') f=-1, ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar(); x*=f; } int n,m,x,y,tot,cnt,lin[N],d[N],seq[N]; bitset<N> f[N]; struct gg { int y,next; }a[N<<1]; inline void add(int x,int y) { a[++tot].y=y; a[tot].next=lin[x]; lin[x]=tot; } void topsort() { queue<int> q; for(int i=1;i<=n;i++) if(!d[i]) q.push(i); while(q.size()) { int t=q.front(); q.pop(); seq[++cnt]=t; for(int i=lin[t];i;i=a[i].next) { int j=a[i].y; if(--d[j]==0) q.push(j); } } } int main() { read(n); read(m); for(int i=1;i<=m;i++) { read(x); read(y); add(x,y); d[y]++; } topsort(); for(int i=cnt;i>=0;i--) { int j=seq[i]; f[j][j]=1; for(int k=lin[j];k;k=a[k].next) f[j]|=f[a[k].y]; } for(int i=1;i<=n;i++) cout<<f[i].count()<<endl; return 0; }
2.小猫爬山
我们每次可以将小猫新租一个缆车,也可以将小猫分配到已经租用过的缆车上;
那么我们关心的状态就是,已经安排好了几只小猫now,已经租用了多少缆车cnt,每辆缆车搭载量的总和;
前两个我们可以作为搜索的状态,最后一个可以用一个数组记录;
对于搜索的每只小猫,我们最多会有cnt+1个分支,,我们尝试将当前now小猫放进i缆车,如果可以,那么我们将该缆车累加搭载量,否则新建一个缆车;
这个我们加入几个剪枝:
1.在搜索是如果发现缆车数大于已有的ans,那么return;
2.我们优先搜索重量大的小猫,这样他的安排选择较少吗,这样可以减少搜索的分支;

#include<bits/stdc++.h> using namespace std; template<typename T>inline void read(T &x) { x=0;T f=1,ch=getchar(); while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} x*=f; } int n,m,cat[20],ans=20,sum[20]; inline void dfs(int u,int k) { if(k>=ans) return ; if(u==n) { ans=k;//有了第一个剪枝,所以无需取min return ; } for(int i=0;i<k;i++) { if(cat[u]+sum[i]<=m) { sum[i]+=cat[u]; dfs(u+1,k); sum[i]-=cat[u];//还原现场 } } sum[k]=cat[u]; dfs(u+1,k+1); sum[k]=0;//还原现场 } int main() { read(n); read(m); for(int i=0;i<n;i++) cin>>cat[i]; sort(cat,cat+n); reverse(cat,cat+n); dfs(0,0); cout<<ans<<endl; return 0; }
毒瘤剪枝来了;
1.优化搜索顺序,在上道题,我们按照重量排序,可以减少搜索分支;
2.排除等效冗余,如果我们发现几条不同的分支,所到达的结果是相同的,我们可以选择只走其中一条;
3.可行性剪枝,明知道这个方案不可能成为最优解,尽早return,这个因题目而异,有时题目会有明显的上下界;
4.记忆化,记录一个状态的答案,在搜索下次直接调用;
接下来我们考虑这些在题目中的体现;
我们先区分一个木棒和木棍;避免下面会迷;
木棒表示拼接好的原始长度,木棍表示截切后的长度,是一段一段的;
我们可以从小到大枚举木棒的长度lenth,sum记录所有木棍的长度总和,那个木棒的个数cnt为sum/lenth,显然必须是一个整数;
对于枚举的每一个len,我们可以依此搜索每根原始木棒由哪些木棍组成;当前需要关心的是已经拼好的木棒个数,正在拼的木棒长度,上一次使用的是哪个木棍;
在每次搜索中,我们尝试用没有使用的的木棍,拼到当前木棒中;
考虑剪枝;
1.优化搜索顺序,我们考虑从大到小搜索木棍,因为较长的木棍能放置的比较有限,可以减少搜索分支;
2.排除等效冗杂,对与当前两个木棍x,y(x>y),先拼x再拼y与先拼y再拼x是等效的;
3.如果在当前原始木棒中第一次使用木棍就失败了,那么直接return;因为再拼这跟木棒时,他和剩余原始木棒是等效的,这个失败,其他的必然失败;
4.如果在拼接当前木棒中放入最后一根木棍恰好完整,而在接下来的分支中返回失败,直接返回失败;用贪心来解释;再用一根木棍恰好拼成一定比用若干木棍拼成更优;
5.我们可以跳过相同长度的木棍;

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<queue> #include<deque> #include<cmath> #include<ctime> #include<cstdlib> #include<stack> #include<algorithm> #include<vector> #include<cctype> #include<utility> #include<set> #include<bitset> #include<map> using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } int stick[70],n,lenth,sum,val; bool st[70]; int used[70]; inline bool dfs(int u,int cur,int start) { if(u*lenth==sum) return true; if(cur==lenth)return dfs(u+1,0,0); for(int i=start;i<n;i++) { if(st[i]) continue; int l=stick[i]; if(cur+l<=lenth) { st[i]=true; if(dfs(u,cur+l,i+1)) return true; st[i]=false; if(!cur) return false; if(cur+l==lenth) return false; int j=i; while(j<n&&stick[j]==l) j++; i=j-1; } } return false; } int main() { while(cin>>n,n) { sum=0,lenth=0; memset(st,false,sizeof(st)); memset(stick,0,sizeof(stick)); for(int i=0;i<n;i++) { int l; cin>>l; stick[i]=l; if(l>50) continue; sum+=l; lenth=max(l,lenth); } sort(stick,stick+n); reverse(stick,stick+n); for(int i=0;i<n;i++) { if(stick[i]>50) { st[i]=true; } } while(true) { if(sum%lenth==0) { if(dfs(0,0,0)) { cout<<lenth<<endl; break; } } lenth++; } } return 0; }
4.生日蛋糕
首先上表面积就是最下底面圆的面积,那么我们在搜索时只需要注意侧面积和高即可;
搜索是我们从下往上搜索,这样比较方便;
搜索状态:当前层数dep,当前外表面积,当前体积;
我们可以枚举高度,半径;当然这是存在枚举上下界的;
由于n−v≥rdep2hdep
有上界:
rdep=min(n−v,rdep+1−1)
hdep=min((n−v)/r2dep,hdep+1−1)
有下界:
rdep=dep,hdep=dep
很明显,ri=i,hi=i是最小的情况,
它们对应的 minsi=2rihi=2i2,minvi=r2ihi=i3
如果当前结果加最小情况超过答案,那么后面就不会有解。
在有解的情况下,有下面不等式成立:
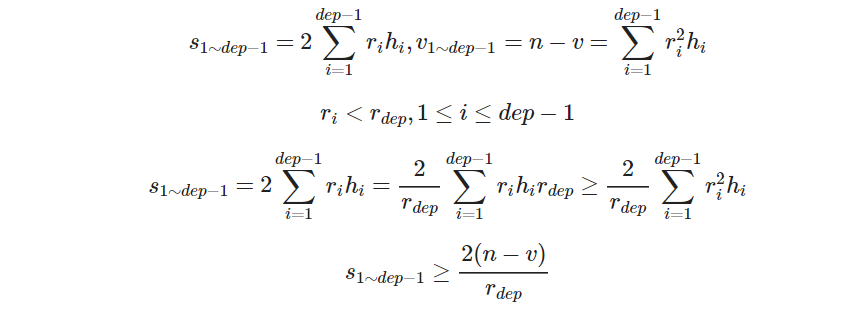
即,2(n−v)rdep 是后面未求面积的下限,如果 2(n−v)rdep+s 大于答案,那么这样的状态是不会更优的。
为了减少搜索分支,我们从大到小枚举;

#include<bits/stdc++.h> using namespace std; template<typename T>inline void read(T &x) { x=0;T f=1,ch=getchar(); while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48); ch=getchar();} x*=f; } const int N=25,INF=1e9; int ans=INF,n,m,R[N],H[N],minv[N],mins[N]; inline void dfs(int dep,int v,int s) { if(s+mins[dep]>ans) return ; if(2*(n-v)/R[dep+1]+s>ans) return ; if(!dep) { if(v==n) ans=s; return ; } for(int r=min((int)sqrt(n-v),R[dep+1]-1);r>=dep;r--) { for(int h=min((n-v)/r/r,H[dep+1]-1);h>=dep;h--) { int t=0; if(dep==m) t=r*r; R[dep]=r,H[dep]=h; dfs(dep-1,v+r*r*h,s+2*r*h+t); } } } int main() { read(n); read(m); for(int i=1;i<=m;i++) { minv[i]=minv[i-1]+i*i*i; mins[i]=mins[i-1]+2*i*i; } R[m+1]=H[m+1]=INF; dfs(m,0,0); if(ans==INF) ans=0; cout<<ans<<endl; return 0; }
又来一个毒瘤:迭代加深:
对于深度优先搜索;有一个明显的缺点就是,一直会搜索到递归的边界才返回,所以对于一些问题,我们如果在一开始就选错了搜索分支,就会在无用的子树中浪费时间;
所谓迭代加深就是限制搜索深度,一旦超过深度就return;
这针对一些搜索深度较浅即可得到答案的搜索;有点类似bfs的按层;
5.加成序列
只有小数据版;
这道题目,n<=100;
所以构造出来的符合题意的m长度最多是10,答案较浅,我们可以考虑迭代加深的做法;
所以对于序列每一个位置,我们可以枚举i,j使x[i]+x[j]==x[k],为了减少搜索分支,我们i,j从大到小枚举;
排除等效冗余:对于不同的i,j,相加的和可能是一样的,我们用一个数组记录这个和是否出现过,出现过不用再搜索;
这里还有一个玄学数学剪枝,我们发现当n>=20的时候;k最小是6;一下就减少了很多搜索;

#include<bits/stdc++.h> using namespace std; const int N=110; int vis[N],x[N],n; inline int dfs(int now,int dep,int last)//当前找到第几个数(深度),dep限制搜索深度,迭代加深; //last记录上次搜索的前两项和,满足数列单调性; { if(x[now]==n) return 1; if(now>=dep) return 0; for(int i=now;i>=1;i--) { for(int j=i;j>=1;j--) { if(!vis[x[i]+x[j]]&&x[i]+x[j]>=last) { x[now+1]=x[i]+x[j]; vis[x[i]+x[j]]=1; if(dfs(now+1,dep,x[i]+x[j])) return 1; vis[x[i]+x[j]]=0; x[now+1]=0;//还原现场; } else if(!vis[x[i]+x[j]]) break;//当前不可能凑出,后面也不可能; } } return 0; } int main() { while(cin>>n,n) { x[1]=1,x[2]=2; int k=n; if(n>2) { if(n>20) k=6;//这个玄学数学剪枝; else k=3; for(;k<=10;k++) { memset(vis,0,sizeof(vis)); memset(x,0,sizeof(x)); x[1]=1,x[2]=2; if(dfs(2,k,3)) break; } } for(int i=1;i<=k;i++) { cout<<x[i]<<' '; } puts(" "); } return 0; }
先不写了奥;



 浙公网安备 33010602011771号
浙公网安备 33010602011771号