二叉堆+哈夫曼树小结

概念：大根堆：树中任意一个节点的权值都小于父节点的权值，小根堆反之：

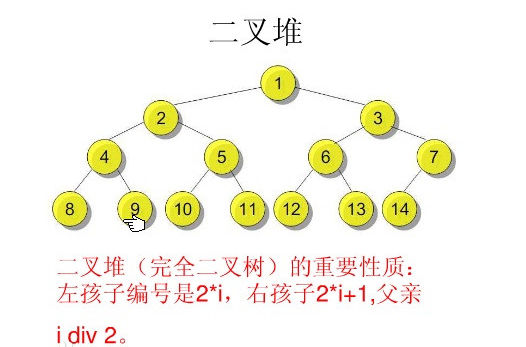
根据完全二叉树的性质：我们储存节点时，左儿子的编号等于父节点编号*2，右儿子编号等于父节点编号*2+1；

c++的stl中的priority_queue（优先队列）为实现一个大根堆，支持push（insert），top( )，pop( ) ，不支持remove，所以感觉很方便，但还是要会手写堆的；

 

第一题：supermarket

贪心：最优解中，对于每个时间t，应该在保证不卖出过期的情况下尽量卖出利润前t大的商品，动态维护这样一个性质；

我们将商品时间排序，见一个小根堆，根节点为商品利润，对于每一个商品；若当前过期时间t大于堆中商品个数，直接插入，若等于，若此时商品利润大于堆顶，则替换堆顶；

#include<bits/stdc++.h>
using namespace std;
int n;
const int maxn = 1e4 + 100;
template<typename T>inline void read(T &x)
{
    x=0;T f=1,ch=getchar();
    while(!isdigit(ch))  {if(ch=='-')  f=-1;  ch=getchar();}
    while(isdigit(ch))  {x=x*10+ch-'0';  ch=getchar();}
    x*=f;
}
pair<int,int> a[maxn];
int main() {
    while(cin>>n) {
        for(int i=1;i<=n;i++) 
            read(a[i].second),read(a[i].first);
        sort(a + 1, a + n + 1);
        priority_queue<int ,vector<int>,greater<int> > q;
        for(int i=1;i<=n;i++) {
            if(a[i].first>q.size()) 
                q.push(a[i].second);
            else if(a[i].first==q.size()&&a[i].second>q.top()) {
                int x=q.top();q.pop();
                q.push(a[i].second);
            }
        }
        int ans=0;
        while(q.size()) {
            ans+=q.top();q.pop();
        }
        cout<<ans<<endl;
    }
    return 0;
}

 

第二题：Sequence

一个M行N列的矩阵，每一行中选一个数，一共取M个，求和，共有N^M中结果，输出前N小个数；

我们可以先做前两个序列一共取两个数得到的和，取前n小，构成一个长度为n序列，然后将得到的新序列与第三个序列合并，以此类推，一共合并M-1次，最后得到的数列就是前n小的和；

对于一个排好序的数列{an}，{bn}（排不排序无所谓）；

得到n个序列：

b1+a1，b1+a2，b1+a3.....，b1+an；

b2+a1，b2+a2，b2+a3.....，b2+an；

b3+a1，b3+a2，b3+a3.....，b3+an；

b4+a1，b4+a2，b4+a3.....，b4+an；

b5+a1，b5+a2，b5+a3.....，b5+an；

、、

bn+a1，bn+a2，bn+a3.....，bn+an；

我们可以开一个小根堆，加入两个元素，一个为权值，一个为当前a的编号；

对于上部分红色部分：我们可以发现它是当前n序列中的最小值，因为an是排好序的，我们将a1+b[i]先加入小根堆中；

假定我们选定b2+a1，为当前第二小，那么我们删掉b2+a1，将它所对应的下一个数b2+a2,加入堆中，进入第三小的选择中，从而保证小根堆中一直只有n个值

每次取出堆顶，那么当前的权值和赋给一个新的数组c,将下一个数加入堆中，我么可以发现下一个元素的取值和为当前的权值和-当前a[p]+a[p+1};

将得到的新数组c赋给a，接着向下一个数组合并；最后a数组存的n个数就是最后的答案；

#include<bits/stdc++.h>
using namespace std;
#define N 2010
typedef pair<int,int> PII;
template<typename T>inline void read(T &x) {
    x=0; T f=1,ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();}
    while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48); ch=getchar();}
    x*=f;
}


int n,m,T,a[N],b[N],c[N];

inline void Union() {
    priority_queue<PII, vector<PII>, greater<PII> > heap;
    for(int i=1;i<=n;i++) heap.push({a[1]+b[i],1});
    for(int i=1;i<=n;i++) {
        PII t=heap.top();
        heap.pop();
        c[i]=t.first;
        heap.push({t.first+a[t.second+1]-a[t.second],t.second+1});
    }
    for(int i=1;i<=n;i++) a[i]=c[i];
}

int main() {
    read(T);
    while(T--) {
        read(m); read(n);
        for(int i=1;i<=n;i++) read(a[i]);
        sort(a+1,a+n+1);
        for(int i=1;i<m;i++) {
            for(int j=1;j<=n;j++) read(b[j]);
            sort(b+1,b+n+1);
            Union();
        }
        for(int i=1;i<=n;i++) printf("%d ",a[i]);
        puts(" ");
    }
    return 0;
}

 

哈夫曼树：

名字挺高级哈，对于一个有i个子节点的k叉树，每个节点对应一个权值wi，要求最小化WPL=Σwi * Li，Li表示该节点到根节点的距离；

为了最小化，我们对于权值大的，尽可能深度较小；

当k==2，我们可以用贪心建出这样一棵树；

1.建一个小根堆，存进去n个节点的权值；

2.取出最小的两个w1，w2，ans+=w1+w2；

3.建一个权值为w1+w2的节点p，并将p插入小根堆中；

4.重复直至堆大小为1，此时ans=Σwi * Li，并且为最小值；

对于k>2时，我们考虑当最后一轮节点数不足以选出k个，这不是最优解，所以我们可以补充添加权值为0的节点，使满足（n-1）mod（k-1）==0，这样执行每次从堆中取出k个的贪心就是正确的；

 

第三题：合并果子；

最终消耗的的体力为果子的质量*合并它的次数，这是一个哈夫曼问题；

对于k==2的情况下，按上述操作即可；

 

#include<bits/stdc++.h>
using namespace std;
priority_queue< int,vector< int >,greater< int > > q;
int n,a,sum;
template<typename T>inline void read(T &x)
{
    x=0;T f=1,ch=getchar();
    while(!isdigit(ch))  {if(ch=='-')  f=-1;  ch=getchar();}
    while(isdigit(ch))  {x=(x<<1)+(x<<3)+(ch^48);  ch=getchar();}
    x*=f;
}
int main() {
    read(n);
    for(int i=1;i<=n;i++)
        read(a),q.push(a);
    for(int i=1;i<n;i++) {
        int x1=q.top();q.pop();
        int x2=q.top();q.pop();
        sum+=x1+x2;
        q.push(x1+x2);
    }
    cout<<sum<<endl;
    return 0;
}

 

第四题：荷马史诗

为了使任意si不是sj的前缀，为满足这个性质：

我们可以使用哈弗曼编码（ n个节点的哈夫曼树含有2n-1个节点，没有度为1的节点 编码从叶子节点到根节点，译码从根节点到叶子节点。），也称为前缀编码；

引例：如果有一需传送的电文为 ‘ABACCDA’，我们可以尝试构建一个二进制串表示，为了保证唯一性，我们需要任意si不是sj的前缀；

我们记录A，B，C，D的出现次数{3,1,2,1};

采用哈夫曼编码；

 

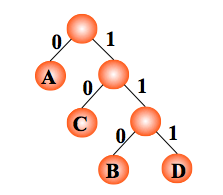
编码： A：0， C：10，  B：110， D：111 。电文 ‘ABACCDA’ 便为 ‘0110010101110’（共 13 位）。

对于本题：我们将每个单词出现的次数作为wi，求出一个k叉哈夫曼树，

那么第一问就是要求出所有叶子结点的WPL，第二问求构造的哈夫曼树最深的深度最小；

第一问就类似合并果子做就可以了，对于第二问，我们只需要在求哈夫曼树时，对于权值相同的点，优先考虑当前深度最小的即可；

 

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
typedef pair<ll,int> PII;
priority_queue<PII,vector<PII>,greater<PII> > heap;
template<typename T>inline void read(T &x) {
    x=0;T f=1,ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x*=f;
}
int n,k;
ll x;
int main() {
    read(n); read(k);
    for(int i=1;i<=n;i++) {
        read(x);
        heap.push(make_pair(x,0));
    }
    while((n-1)%(k-1)) heap.push(make_pair(0,0)),n++;
    ll res=0;
    while(heap.size()>1) {
        int depth=0;
        ll s=0;
        for(int i=1;i<=k;i++) {
            PII t=heap.top();
            heap.pop();
            s+=t.first;
            depth=max(depth,t.second);    
        }
        res+=s;  
        heap.push(make_pair(s,depth+1));
    }
    cout<<res<<endl<<heap.top().second<<endl;
    return 0;
}

 

还是要学习：

你的问题在于读书不多而想的太多。——杨绛。