线段树模板

我死辽为什么板子那么难调awsl

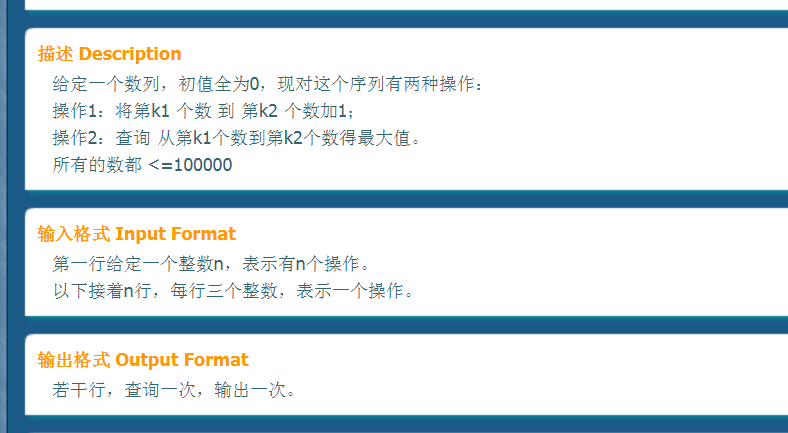
第一题：

 

注意空间要开4倍，写位运算的话左移右移不要打错啊；

#include<bits/stdc++.h>
using namespace std;
#define N 500010
const int inf = 0x3f3f3f3f;
template<typename T>inline void read(T &x)
{
    x=0;T f=1,ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x*=f;
}
struct gg
{
    int l,r,dat;
}tre[N*4];
int a[N],n,m,x,y,ty; 
inline void build(int p,int l,int r)
{
    tre[p].l=l,tre[p].r=r;
    if(l==r) {tre[p].dat=a[l];return ;}
    int mid=(l+r)>>1;
        build(p<<1,l,mid);
    build(p<<1|1,mid+1,r);
    tre[p].dat=max(tre[p<<1].dat,tre[p<<1|1].dat);
}
inline void change(int p,int x,int v)
{
    if(tre[p].l==tre[p].r) {tre[p].dat=v;return ;}
    int mid=(tre[p].l+tre[p].r)>>1;
    if(x<=mid) change(p<<1,x,v);
    else  change(p<<1|1,x,v);
    tre[p].dat=max(tre[p<<1].dat,tre[p<<1|1].dat);
}
inline int ask(int p,int l,int r)
{
    if(l<=tre[p].l&&r>=tre[p].r)  return tre[p].dat;
    int mid=(tre[p].l+tre[p].r)>>1;
    int val=-inf;
    if(l<=mid) val=max(val,ask(p<<1,l,r));
    if(r>mid)  val=max(val,ask(p<<1|1,l,r));
    return val;
}
int main()
{
    read(n);
    memset(a, 0, sizeof(a));
    build(1, 1, n);
    for(int i=1;i<=n;i++)
    {
        read(ty);read(x);read(y);
        if(ty==1)change(1,x,y);
        else
        {
            printf("%d\n",ask(1,x,y));
        }
    }
    return 0;
} 

第二题：

先说一下延迟标记吧，在线段树的区间查询指令中，每当遇到被查询的区间[L,R]完全覆盖的节点时，,可以立即把该节点上储存的信息作为候选答案返回，他会被分为O（lodN）个小区间，不过，在区间修改时，每当遇到被查询的区间[L,R]完全覆盖的节点时，那么以该节点为根的整棵子树，所以复杂度都会升到O（N）；

我们可以对于每个结点增加一个属性:int add;add记录的是此节点所代表的区间所有数被加的值

每一个节点新添加一个标记，记录这个节点是否进行了某种改动(这样的改动操作会影响其子节点)，对于随意区间的改动，我们先依照区间查询的方式将其划分成线段树中的节点，然后改动这些节点的信息，并给这些节点标记上代表这样的改动操作的标记。在改动和查询的时候，假设我们到了一个节点p，而且决定考虑其子节点，那么我们就要看节点p是否被标记，若设有，就要依照标记改动其子节点的信息，而且给子节点都标上同样的标记，同一时候消掉节点p的标记。这样每条查询和修改都是O（logN）了；

注释在代码;

 

#include<bits/stdc++.h>
using namespace std;
#define l(x) tre[x].l
#define r(x) tre[x].r
#define sum(x) tre[x].sum
#define add(x) tre[x].add 
#define dat(x) tre[x].dat
template<typename T>inline void read(T &x)
{
    x=0;T f=1,ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch))  {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x*=f;
}
struct gg
{
    int l,r,dat;
    long long sum,add;//sum是区间和，add是增量延迟标记； 
    
}tre[2000010];
int a[1000010],n,m,op,l,r,d;

inline void build(int p,int l,int r)
{
    l(p)=l;r(p)=r;
    if(l==r) {dat(p)=a[l];return ;}
    int mid=l+r>>1;
    build(p<<1,l,mid);
    build(p<<1|1,mid+1,r);
    dat(p)=max(dat(p<<1),dat(p<<1|1));
    sum(p)=sum(p<<1)+sum(p<<1|1); 
}
inline void spread(int p)
{
    if(add(p))//如果p点有标记
    {
        sum(p<<1)+=add(p)*((r(p<<1))-l(p<<1)+1);//更新左节点信息； 
        sum(p<<1|1)+=add(p)*(r(p<<1|1)-l(p<<1|1)+1);//更新右节点信息；
        add(p<<1)+=add(p);//给左节点左做延迟标记 
        add(p<<1|1)+=add(p); //给右节点做延迟标记 
        dat(p<<1)+=add(p);
        dat(p<<1|1)+=add(p);
        add(p)=0;//清除p的标记； 
    } 
}
inline void change(int p,int l,int r,int d)
{
    if(l<=l(p)&&r>=r(p))
    {
        sum(p)+=(long long)d*(r(p)-l(p)+1);
        add(p)+=d;
        dat(p)+=d;
        return ;
    }
    spread(p);
    int mid=(l(p)+r(p))>>1;
    if(l<=mid) change(p<<1,l,r,d);
    if(r>mid) change(p<<1|1,l,r,d);
    sum(p)=sum(p<<1)+sum(p<<1|1);
    dat(p)=max(dat(p<<1),dat(p<<1|1)); 
} 
inline long long ask(int p,int l,int r)
{
    if(l<=l(p)&&r>=r(p))    return dat(p);
    spread(p);
    int mid=(l(p)+r(p))>>1;
    long long val=-(1<<30);
    if(l<=mid) val=max(val,ask(p<<1,l,r));
    if(r>mid) val=max(val,ask(p<<1|1,l,r));
    return val; 
}
int main()
{
    read(m);
    build(1,1,m);
    for(int i=1;i<=m;i++)
    {
        read(op);
        if(op==1)
        {
            read(l);read(r);
            change(1,l,r,1);
        }
        else
        {
            read(l);read(r);
            printf("%d\n",ask(1,l,r));
        }
    }
    return 0;
}