D6差分及树上差分
原谅我这篇博客拖了很久才写;
来到学校就和白痴一样缺了一世纪的课 上课特别懵;还有开学考枯了;
差分有列的差分,对于一段区间【l,r】进行修改,显然如果我们对于他的差分数组的l和r+1进行修改就可以了;
Xni=1a[i]
=(c[1]) + (c[1] + c[2]) + · · · + (c[1] + c[2] + · · · + c[n])
= n × c[1] + (n − 1) × c[2] + · · · + c[n]= n × (c[1] + c[2] + · · · + c[n])− (0 × c[1] + 1 × c[2] + · · · + (n − 1) × c[n])
所以,我们维护一个数组c2[i] = (i − 1) × c[i]在将区间[l,r] 的数全部+v 则还需同时将c2[l] + v × (i − 1), c2[r + 1] + (−v) × r 。
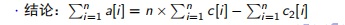
树上差分:分为点的差分和边的差分;
点的差分:
在一棵n个结点的树中,形容从si走到到ti的要求,求这条路径上的点被经过的次数。
显然,我们需要找到他们的LCA(中转点)。
我们需要让cnt[s] + +,让cnt[t] + +,而让他们的cnt[lca] − −,cnt[faher[lca]] − −;
最终统计即可;
边的差分不太一样;cnt[s] + +, cnt[t] + +, cnt[LCA]− =2;仔细画图理解一下;
第一题:BZOJ 4390
树上差分的模板题:

#include<bits/stdc++.h> using namespace std; const int maxn=5e4+10; template<typename T>inline void read(T &x) { x=0; T f=1,ch=getchar(); while (!isdigit(ch)) ch=getchar(); if (ch=='-') f=-1, ch=getchar(); while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar(); x*=f; } int ver[maxn<<1],Next[maxn<<1],head[maxn],len; inline void add(int x,int y) { ver[++len]=y,Next[len]=head[x],head[x]=len; } int fa[maxn],d[maxn],f[maxn][21]; inline void dfs1(int x,int father,int deep) { fa[x]=father,d[x]=deep; for (int i=1;i<16;++i) f[x][i]=f[f[x][i-1]][i-1]; for (int i=head[x];i;i=Next[i]) { int y=ver[i]; if (y==father) continue; f[y][0]=x; dfs1(y,x,deep+1); } } inline int lca(int x,int y) { if (d[x]>d[y]) swap(x,y); for (int i=15;i>=0;--i) if (d[f[y][i]]>=d[x]) y=f[y][i]; if (x==y) return x; for (int i=15;i>=0;--i) if (f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } int siz[maxn],sum[maxn],ans; inline void dfs2(int x,int father) { siz[x]=sum[x]; for (int i=head[x];i;i=Next[i]) { int y=ver[i]; if (y==father) continue; dfs2(y,x); siz[x]+=siz[y]; } ans=max(ans,siz[x]); } int main() { int n,k; read(n);read(k); for (int i=1;i<n;++i) { int x,y; read(x);read(y); add(x,y);add(y,x); } dfs1(1,0,1); for (int i=1;i<=k;++i) { int a,b; read(a);read(b); int c=lca(a,b); ++sum[a],++sum[b],--sum[c]; if (c!=1) --sum[fa[c]]; } dfs2(1,0); printf("%d\n",ans); return 0; }
第二题:POJ 3417
题目大意:一棵有N个点的树,再往里面加入M条新边,现在要破坏其中的两条边,要求一条是原来树中的边,一条是新边,使其不连通。求方案的数量。
1 ≤ N ≤ 100000), 1 ≤ M ≤ 100000)
算法进阶好像也有;对于新加的一条边来说,肯定会与之前的树形成一个环,而此时环内的树上边和新加的这条边一同删除就会是一种方案。
而这道题是将所有新边都加入后的情况,那么我们看每条边,如果没有与它形成环的情况,那么这条边删除肯定会使得图不连通,即情况就会加M,也就是和新加的M条边任意组合都可以。
因而我们每次读入一条附加边,就给x到y的路径上的所有主要边记录上“被覆盖一次”,对于我们想要切割的一条主要边,有以下3种情况
1 若这条边被覆盖0次,则可以任意再切断一条附加边。
2 若这条边被覆盖1次,那么只能再切断唯一的一条附加边。
3 若这条边被覆盖2次及以上,没有可行的方案;
树上差分写一下;

#include<algorithm> #include<bitset> #include<cctype> #include<cerrno> #include<clocale> #include<cmath> #include<complex> #include<cstdio> #include<cstdlib> #include<cstring> #include<ctime> #include<deque> #include<exception> #include<fstream> #include<functional> #include<limits> #include<list> #include<map> #include<iomanip> #include<ios> #include<iosfwd> #include<iostream> #include<istream> #include<ostream> #include<queue> #include<set> #include<sstream> #include<stack> #include<stdexcept> #include<streambuf> #include<string> #include<utility> #include<vector> #include<cwchar> #include<cwctype> using namespace std; const int maxn=1e5+10; template<typename T>inline void read(T &x) { x=0; T f=1,ch=getchar(); while (!isdigit(ch)) ch=getchar(); if (ch=='-') f=-1, ch=getchar(); while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar(); x*=f; } int ver[maxn<<1],Next[maxn<<1],head[maxn],len; inline void add(int x,int y) { ver[++len]=y,Next[len]=head[x],head[x]=len; } int fa[maxn],d[maxn],f[maxn][21]; inline void dfs1(int x,int father,int deep) { fa[x]=father,d[x]=deep; for (int i=1;i<=20;++i) f[x][i]=f[f[x][i-1]][i-1]; for (int i=head[x];i;i=Next[i]) { int y=ver[i]; if (y==father) continue; f[y][0]=x; dfs1(y,x,deep+1); } } inline int lca(int x,int y) { if (d[x]>d[y]) swap(x,y); for (int i=20;i>=0;--i) if (d[f[y][i]]>=d[x]) y=f[y][i]; if (x==y) return x; for (int i=20;i>=0;--i) if (f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } int siz[maxn],sum[maxn],ans; inline void dfs2(int x,int father) { siz[x]=sum[x]; for (int i=head[x];i;i=Next[i]) { int y=ver[i]; if (y==father) continue; dfs2(y,x); siz[x]+=siz[y]; } } int main() { int n,m; read(n);read(m); for (int i=1;i<n;++i) { int x,y; read(x);read(y); add(x,y);add(y,x); } dfs1(1,0,1); for (int i=1;i<=m;++i) { int a,b; read(a);read(b); int c=lca(a,b); ++sum[a],++sum[b],sum[c]-=2; } dfs2(1,0); for (int i=1;i<=n;++i) if (!siz[i] && i!=1) ans+=m; else if (siz[i]==1) ++ans; printf("%d\n",ans); return 0; }
第三题:LUOGU CF 739B
如果v可以控制u,那么从v到u的路上的所有结点都可以控制u,因为从v到u路上的dist(v, u)是递减的。
可以每次遍历一个点的时候,二分找出根节点到当前点i路径上点,找出dist(j, i)刚好大于a[i]的点,树上差分统计这条路径。
而后遍历当前点i的所有儿子结点k,cnt[i]+ = cnt[k]
这里我写了倍增;

#include<bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=2e5+10; template<typename T>inline void read(T &x) { x=0; register int f=1; register char ch=getchar(); while (!isdigit(ch)) { if (ch=='-') f=-1; ch=getchar();} while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar(); x*=f; } template<typename T>inline void print(T x) { if (x<0) putchar('-'),x=-x; if (x>9) print(x/10); putchar(x%10+48); } int ver[maxn<<1],edge[maxn<<1],Next[maxn<<1],head[maxn],len; inline void add(int x,int y,int z) { ver[++len]=y,edge[len]=z,Next[len]=head[x],head[x]=len; } ll d[maxn];//必须用long long,否则过不了,如果你想一直莫名WA的话,可以不管 int f[maxn][19]; int a[maxn]; int ans[maxn]; inline void dfs(int x,int fa,int dist) { d[x]=d[fa]+dist,f[x][0]=fa; for (int i=1;i<=18;++i) f[x][i]=f[f[x][i-1]][i-1]; for (int i=head[x];i;i=Next[i]) { int y=ver[i],z=edge[i]; if (y==fa) continue; dfs(y,x,z); register int val=a[y],k=1,now=y; while (k&&now) { if (d[now]-d[f[now][k]]<=val) { val-=d[now]-d[f[now][k]]; now=f[now][k]; k<<=1; } else k>>=1; } if (d[now]-d[f[now][0]]<=val) now=f[now][0]; --ans[f[now][0]],++ans[f[y][0]]; } ans[fa]+=ans[x]; } int main() { int n,y,z;read(n); for (int i=1;i<=n;++i) read(a[i]); for (int i=2;i<=n;++i) { read(y);read(z); add(i,y,z);add(y,i,z); } dfs(1,0,0); for (int i=1;i<=n;++i) print(ans[i]),putchar(' '); return 0; }
借教室:luoguP1083
二分能满足的订单数。差分数组,对于二分的一个值,先差分到当前订单,扫描维护前缀和即为当前借的教室数与d作比较即可;

#include <algorithm> #include <cctype> #include <cmath> #include <complex> #include <cstdio> #include <cstring> #include <deque> #include <functional> #include <list> #include <map> #include <iomanip> #include <iostream> #include <set> #include <queue> #include <stack> #include <string> #include <vector> #define sys system("PAUSE") using namespace std; const int maxn = 1e6 + 1000; typedef long long ull; inline int read() { int x=0,f=1; char ch=getchar(); while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} return x*f; } int n, m,a[maxn],d[maxn],r[maxn],l[maxn],c[maxn],sum[maxn],begin,end; inline bool check(int k) { memset(c, 0, sizeof(c)); for(int i=1;i<=k;++i) { c[l[i]]+=d[i]; c[r[i]+1]-=d[i]; } for(int i=1;i<=n;++i) { sum[i]=sum[i-1]+c[i]; if(sum[i]>a[i]) return false; } return true; } int main() { n=read(),m=read(); for (int i=1;i<=n;++i) a[i]=read(); for (int i=1;i<=m;++i) d[i]=read(),l[i]=read(),r[i]=read(); begin=1,end=m; if(check(m)) { printf("0\n"); return 0; } while(begin<end) { int mid=(begin+end)>>1; if(check(mid)) begin=mid+1; else end=mid; } printf("%d\n%d\n",-1,begin); return 0; }
好啦我要去学生物必修二的什么自由组合蒙圈题了,毕竟还有琵琶行等我背呢;



