MAP-Elites
原文:https://www.cnblogs.com/Twobox/p/16836104.html
背景动机
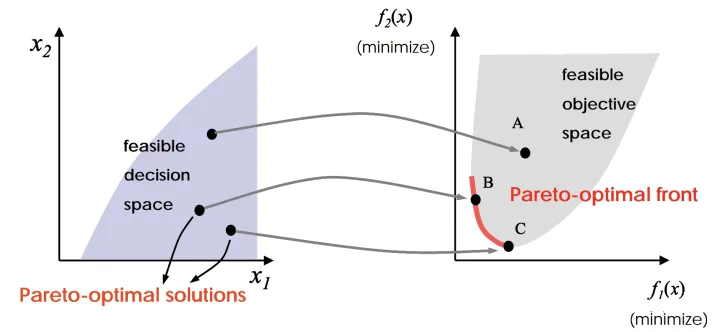
大多数搜索算法专注于在搜索空间中寻找一个或一小组高质量的解决方案。用户指定了解决方案应该追求的一个或几个目标。例如,用户可能需要高性能和低成本的解决方案。传统的搜索算法包括爬山、模拟退火、进化算法、梯度上升/下降、贝叶斯优化和多目标优化算法等。
1、多样性问题
黑盒优化中的一大挑战就是局部最优,特别是在高度欺骗性的问题。因为在这些问题中,必须跨越低性能的山谷来找到全局最优。
而一个重要的解决方案就是保持种群的多样性,来获得最终更高的性能。但仍然倾向于在早期收敛到一个或几个好的解决方案。
2、另一种搜索需求
搜索一组解,在追求高性能的同时,解之间的特征保持多样性。例如在强化学习中我想训练一组高性能策略,但是这些策略需要有不同的倾向,例如有些激进有些保守,有些注重通关时间,有些注重积分获得。
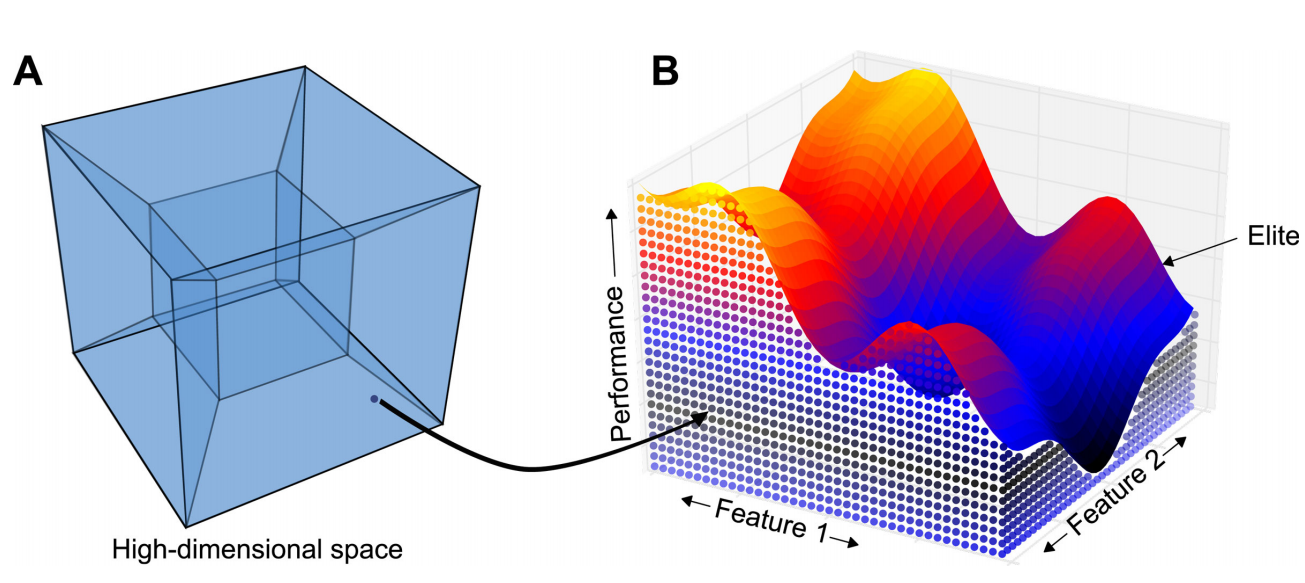
如下图,我要在最求高性能的同时,在Feature_1和Feature_2上各异的一堆解。看这座山中的每一个点。
提出算法

准备过程:
1、首先确定性能度量 \(f(x)\),例如是某种策略的最终奖励,就是优化中的目标函数
2、其次选择N个关注的特征,例如策略的速度、激进程度等
3、特征一般是连续的,在考虑计算资源的情况下,需要进行离散化。
算法流程:
初始化:首先随机生成一定数量个体,并确定每个个体的性能值和特征值。并将这些个体放在特征空间中所属的格子中(如果多个映射到同一个格子,那么性能表现最高的一个将被保留)。
然后重复以下步骤,直到达到终止标准:
1、在map中随机选择一个个体,通过交叉或变异生产一个后代。
2、确定该后代的性能和特征,并找到对应的特征方格
3、如果格子为空,则直接放入。如果非空,则保留更优秀的。
终止条件:
终止条件可以是多方面:例如 时间结束、消耗完固定数量的计算资源、或者性能达到某种水平等。
两点改进:
1、离散化的粒度可以手动指定或自动调整到可用的资源,包括从粗粒度开始,然后在时间和计算允许的情况下减小粒度。
2、很适合并行化,并行生成与评估节点。
算法性能评价
1、Global Performance:该算法的最优个体的性能值 除以 现所有算法能达到的最高性能值
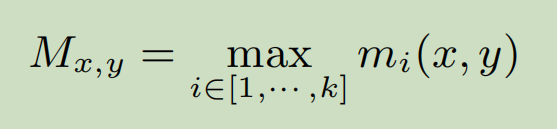
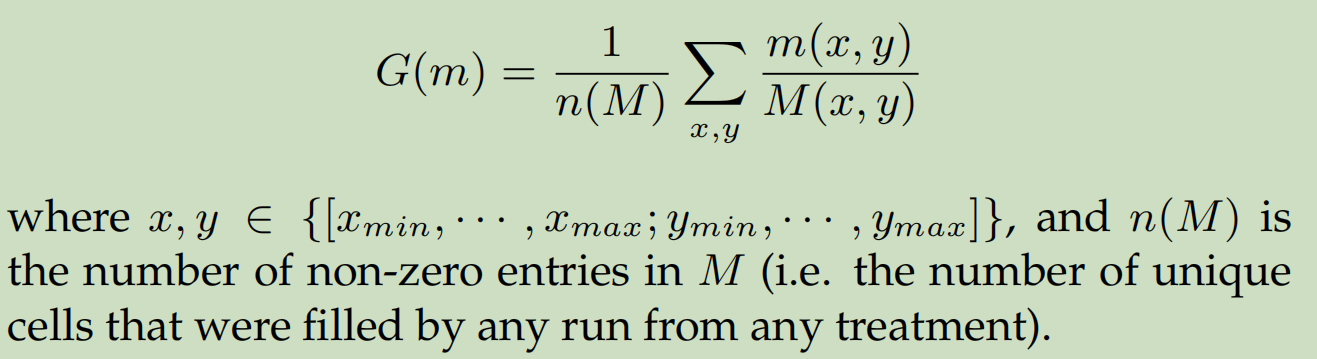
2、Global reliability:该算法,每个格子的最大性能 除以 现所有算法该格子的最大性能。之后求和取平均
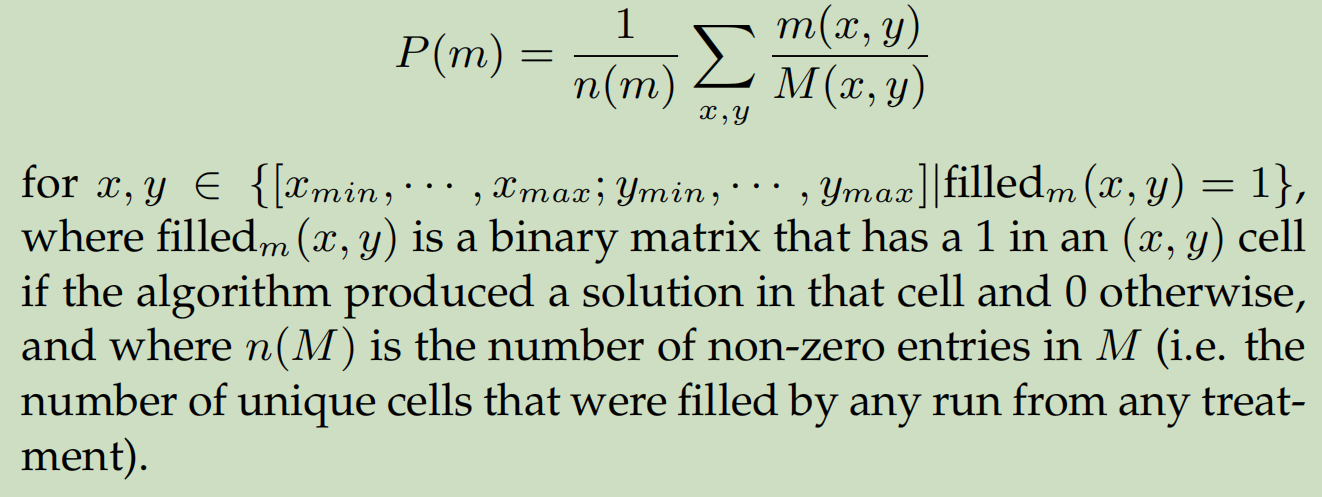
3、Precision(opt-in reliability):与Global reliability类似,只不过只有该算法填充过的格子才参与计算。所以分数会比第二个高。例如先所有算法最优情况能够填充100个格子,该算法填充了90个格子,那么只有这90个格子参与计算。而评价2则是100个格子参与计算。
4、 Coverage:该算法覆盖格子数,除以 所有算法最大覆盖格子数
实验效果
做了三个实验,分别是:
neural networks, simulated soft robot morphologies, and a real, soft robotic arm
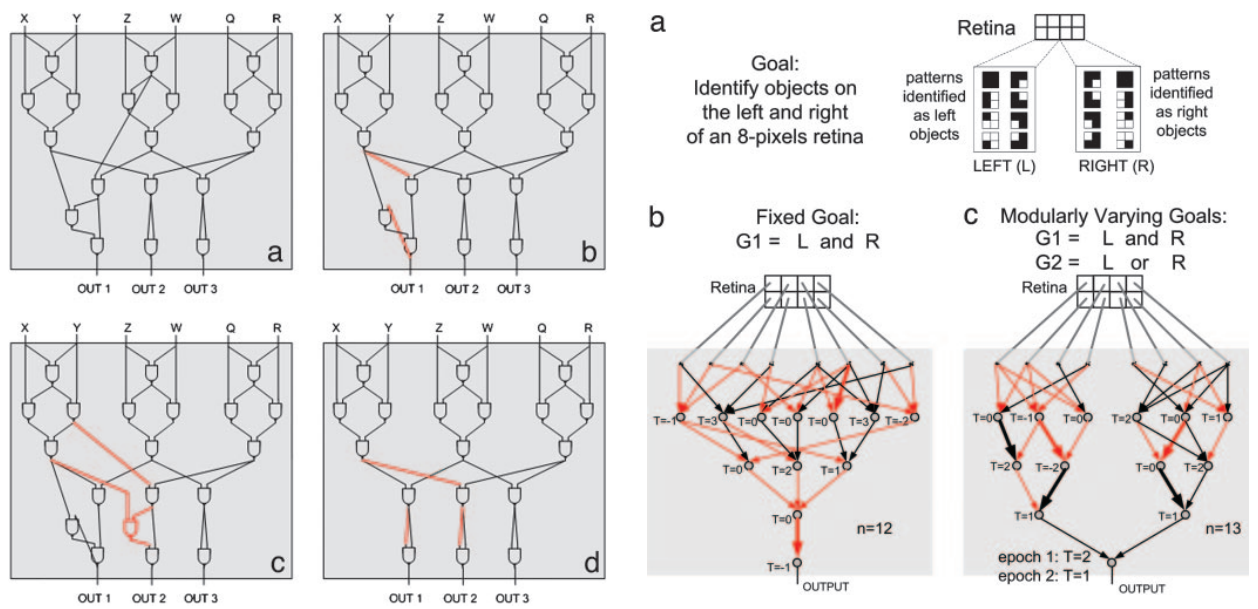
1、神经网络
2、模拟软机器人
3、真实软机械臂
前两个搜索空间(神经网络和模拟软机器人)是非常高维的,这展示了该算法从高维搜索空间中创建低维特征地图的能力。
结果:
上面四幅图,展示的是分别在上述四个指标下的情况。我们看到该算法对该问题的效果都是最优的。
值得注意的是,即使该算法只关注整体上的优化,但最优结果也优于传统的EA。这可能是因为测试问题具有欺骗性,而传统的进化算法对多样性压力不够,而进一步的多样性有助于消除欺骗。
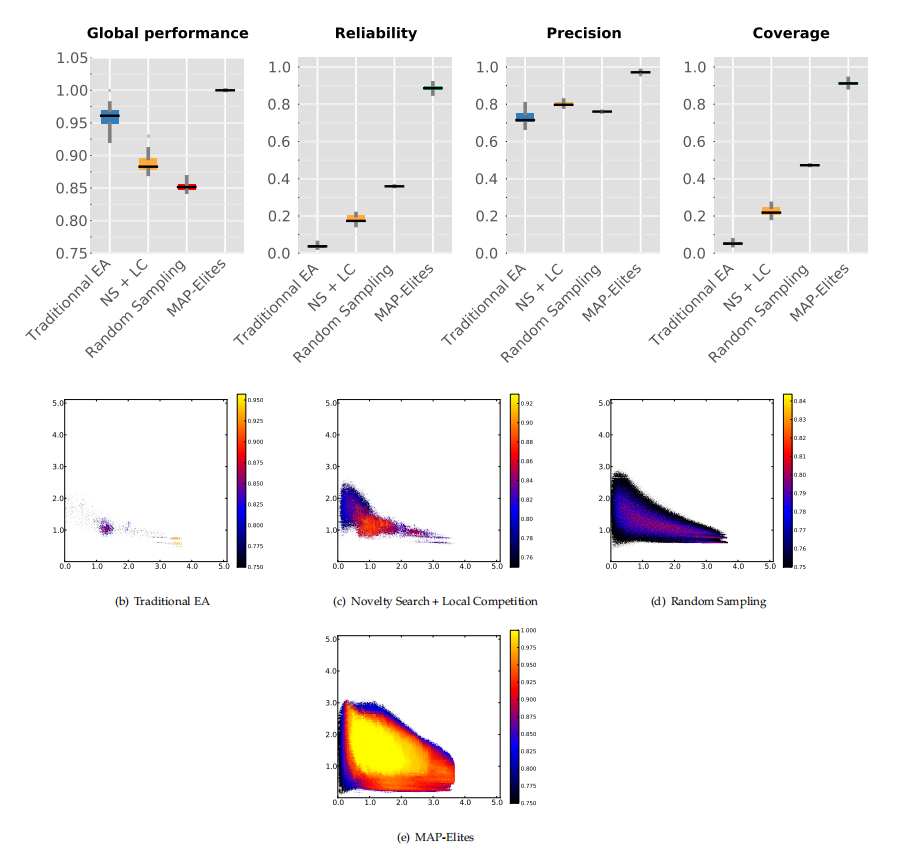
下面四幅图。x、y轴分别是定义的2个特征偏好,热图颜色表示标准化性能。这些地图显示,该算法照亮了更多的特征空间,揭示了每个区域的适应度潜力。
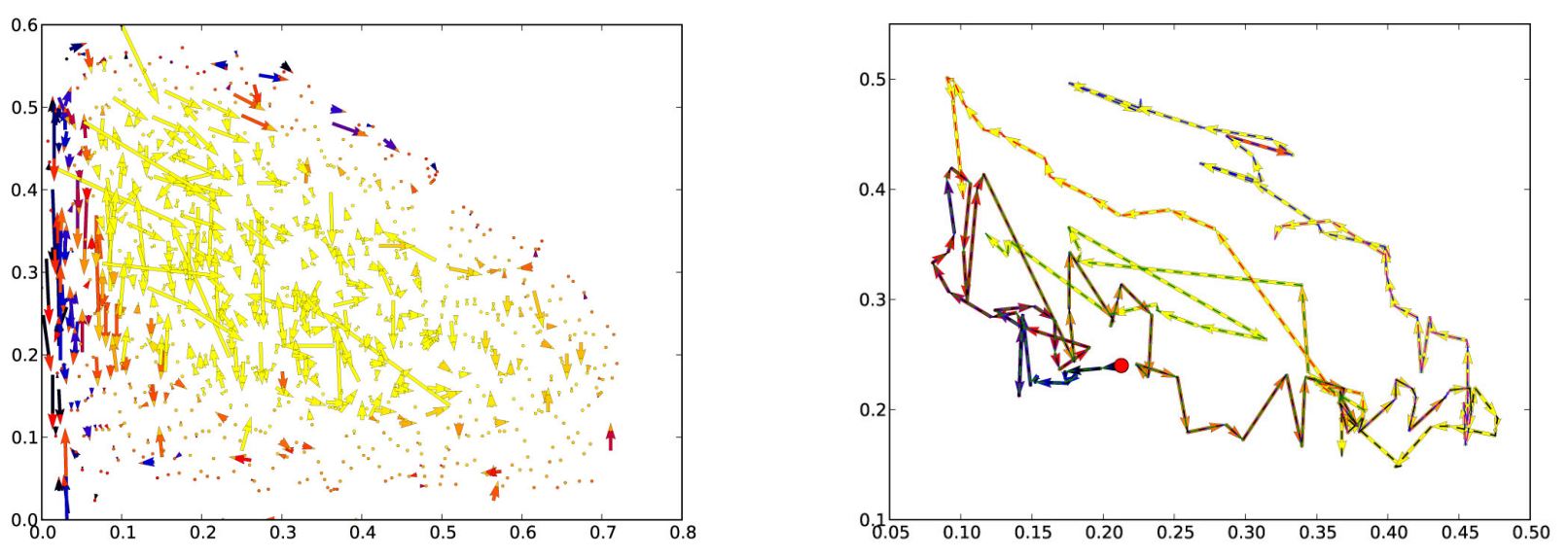
进一步分析:
左图:每一个箭头,表示新精英个体产生情况。值得注意的是,许多高性能精英来自其他高性能精英,但通常不是来自直接的相邻个体。
这些数据表明,在许多不同的地点收集高绩效的精英有助于在新的地点发现高绩效的精英,这可能就是为什么地图精英能够找到这么多不同的、高性能的解决方案的原因。即他不只是在局部优化打转,而是能够发散开来。
右图:跟踪了四条精英的产生路线,对应四种不同颜色的轨迹(绿色、橙色、蓝色、紫色),他们起点都是红点的那个初始精英。我们会发现,它经常穿过地图的许多不同区域。例如红色的那条就比较明显。
优势总结
- 允许用户在他们所选择的变化维度中创建多样性。
- 阐明整个特征空间的适应度潜力,而不仅仅是高性能区域,揭示感兴趣的维度和性能之间的关系。
- 改进优化性能;在复杂的搜索空间中,它探索了更多的特征空间,进一步避免局部优化,从而找到不同的,通常更好的适应度峰值。
- 在任何单个属性组合中搜寻新的解决方案,都有助于同时在其他属性组合中寻找解决方案。
- 最终结果返回大量不同的、高性能的个体,有助于用来创建新类型的算法或提高现有算法的性能





