NSGA2、NSGA-II实现、基于分配的多目标进化-Python
算法流程:
P:父辈种群
Q:子辈种群
R:P并上Q -》 之后依据偏序关系进行排序
在实际上,能在原来数组上改就到原来数组上改,要产生新的那就产生新的,分配一次内存时间应该影响不大,以后再考虑底层优化。!
在函数调用上,一律认为创建了一个新的数组
初始化:P
计算P适应度:F
根据适应度度计算层次关系:rank、L
# rank为P对应的等级数组,L标记每层的元素数量
根据F、rank计算拥挤距离,越大越好:crowding_distance
更具rank, crowding_distance对dna进行排序:得到新P
对P按序号两两进行单点交叉:得Q
对Q按概率做一遍变异:新Q
将P、Q复制到R中
重复计算适应度开始重新
交叉使用单点交叉: pc = 0.9
变异概率:1/决策变量数 或 1/二进制编码长度
250代
1 # nsga2.py 2 import numpy as np 3 4 5 class individual: 6 def __init__(self, dna): 7 self.dna = dna 8 self.dna_len = len(dna) 9 10 self.f = None 11 self.rank = -1 12 self.crowding_distance = -1 # 越远 多样性越好 13 14 def __gt__(self, other): 15 if self.rank > other.rank: 16 return True 17 if self.rank == other.rank and self.crowding_distance < other.crowding_distance: 18 return True 19 return False 20 21 def get_fitness(self, F): 22 len_F = len(F) 23 fitness = np.zeros(shape=len_F) 24 for i in range(len_F): 25 fitness[i] = F[i](self.dna) 26 return fitness 27 28 def cross_newObj(self, p1, p2): 29 # 不能修改之前的,需要生成一个新的对象 30 p1_dna = p1.dna.copy() 31 p2_dna = p2.dna.copy() 32 cut_i = np.random.randint(1, self.dna_len - 1) 33 temp = p1_dna[cut_i:].copy() 34 p1_dna[cut_i:] = p2_dna[cut_i:] 35 p2_dna[cut_i:] = temp 36 37 q1 = individual(p1_dna) 38 q2 = individual(p2_dna) 39 40 return q1, q2 41 42 def cross(self, p1, p2): 43 cut_i = np.random.randint(1, self.dna_len - 1) 44 temp = p1[cut_i:].copy() 45 p1[cut_i:] = p2[cut_i:] 46 p2[cut_i:] = temp 47 return p1, p2 48 49 def mutation(self, domain): 50 point = np.random.randint(0, self.dna_len) 51 low = domain[point][0] 52 high = domain[point][1] 53 self.dna[point] = np.random.rand() * (high - low) + low 54 return self.dna 55 56 def dominate(self, p2): 57 p1 = self 58 # p1 是否支配p2 59 dominated = True 60 for i in range(len(p1.f)): 61 if p1.f[i] > p2.f[i]: 62 dominated = False 63 break 64 return dominated 65 66 67 class nsga2: 68 def __init__(self, pop_size, dna_size, pc, pm, f_funcs, domain): 69 self.pop_size = pop_size 70 self.dna_size = dna_size 71 self.f_size = len(f_funcs) 72 self.pc = pc 73 self.pm = pm 74 self.f_funcs = f_funcs 75 self.domain = domain 76 77 def ini_pop(self): 78 P_dna = np.random.random(size=(self.pop_size, self.dna_size)) 79 for i in range(len(self.domain)): 80 item = self.domain[i] 81 P_dna[:, i] = P_dna[:, i] * (item[1] - item[0]) + item[0] 82 83 P = [] # 初始种群P 84 for dna in P_dna: 85 P.append(individual(dna)) 86 87 return P 88 def calculate_pop_fitness(self, pop): 89 # 计算Pop适应度,存储到individual中 90 for p in pop: 91 p.f = p.get_fitness(self.f_funcs) 92 return pop 93 94 def fast_non_dominated_sort(self, R): 95 # 非支配排序操作 96 # 默认调用之前,改执行的动作已经执行过了 97 R_len = len(R) 98 n = np.zeros(shape=R_len) # 被支配数 99 S = [] # 支配了那些成员 100 F = [[]] # 每层个体编号(对R) 101 for i in range(R_len): 102 Sp = [] 103 n[i] = 0 104 for j in range(R_len): 105 if i == j: 106 continue 107 if R[i].dominate(R[j]): 108 Sp.append(j) 109 elif R[j].dominate(R[i]): 110 n[i] += 1 111 S.append(Sp) 112 if n[i] == 0: 113 R[i].rank = 0 114 F[0].append(i) 115 116 i = 0 117 while len(F[i]) != 0: 118 Q = [] # i+1层 119 for p in F[i]: 120 for q in S[p]: 121 n[q] -= 1 122 if n[q] == 0: 123 R[q].rank = i + 1 124 Q.append(q) 125 i += 1 126 F.append(Q) 127 F.pop() 128 129 # 转化为实际的人 130 F_obj = [] 131 for rank in F: 132 rank_obj = [R[p_idx] for p_idx in rank] 133 F_obj.append(rank_obj) 134 135 return F_obj # 每层包含的实际的人 136 137 def crowding_distance_pop(self, F): 138 for rank in F: 139 self.crowding_distance_assignment(rank) 140 141 def crowding_distance_assignment(self, rank): 142 # 初始化该组所有人的距离为0 143 pop_fitness = [] 144 for p in rank: 145 p.crowding_distance = 0 146 pop_fitness.append(p.f) 147 pop_fitness = np.array(pop_fitness) 148 sorted_idx = np.argsort(pop_fitness, axis=0) 149 f_dimension = len(self.f_funcs) 150 for i in range(f_dimension): 151 # 在f1下是适应度的排序 152 fi_sort_idx = sorted_idx[:, i] 153 fi_sort_p = [rank[i] for i in fi_sort_idx] 154 # fi_sort_p = rank[fi_sort_idx] 155 inf = 9999999999999 156 fi_sort_p[0].crowding_distance = fi_sort_p[-1].crowding_distance = float(inf) 157 diff = fi_sort_p[-1].f[i] - fi_sort_p[0].f[i] 158 for j in range(1, len(fi_sort_p) - 1): 159 a = fi_sort_p[j + 1].f[i] 160 # fi_sort_p[j].crowding_distance += (fi_sort_p[j + 1].f[i] - fi_sort_p[j - 1].f[i]) / diff 161 fi_sort_p[j].crowding_distance += (fi_sort_p[j + 1].f[i] - fi_sort_p[j - 1].f[i]) 162 163 # 打印看下 164 return rank 165 166 def select(self, R): 167 R.sort() 168 # print(len(R)) 169 # print([[p.rank, p.crowding_distance] for p in R]) 170 return R[:self.pop_size] 171 172 def pop_cross(self, P): 173 new_Q = [] 174 i = 0 175 P_len = len(P) 176 while i < P_len: 177 q1, q2 = P[i].cross_newObj(P[i], P[i + 1]) 178 new_Q.append(q1) 179 new_Q.append(q2) 180 i += 2 181 return new_Q 182 183 def pop_mutation(self, Q): 184 for q in Q: 185 if np.random.rand() < self.pm: 186 q.mutation(self.domain) 187 return Q
1 # zdt_funcs.py 2 import numpy as np 3 4 5 def zdt4_f1(x_list): 6 return x_list[0] 7 8 9 def zdt4_gx(x_list): 10 sum = 1 + 10 * (10 - 1) 11 for i in range(1, 10): 12 sum += x_list[i] ** 2 - 10 * np.cos(4 * np.pi * x_list[i]) 13 return sum 14 15 16 def zdt4_f2(x_list): 17 gx_ans = zdt4_gx(x_list) 18 if x_list[0] < 0: 19 print("????: x_list[0] < 0:", x_list[0]) 20 if gx_ans < 0: 21 print("gx_ans < 0", gx_ans) 22 if (x_list[0] / gx_ans) <= 0: 23 print("x_list[0] / gx_ans<0:", x_list[0] / gx_ans) 24 25 ans = 1 - np.sqrt(x_list[0] / gx_ans) 26 return ans 27 28 29 def zdt3_f1(x): 30 return x[0] 31 32 33 def zdt3_gx(x): 34 if x[:].sum() < 0: 35 print(x[1:].sum(), x[1:]) 36 ans = 1 + 9 / 29 * x[1:].sum() 37 return ans 38 39 40 def zdt3_f2(x): 41 g = zdt3_gx(x) 42 ans = 1 - np.sqrt(x[0] / g) - (x[0] / g) * np.sin(10 * np.pi * x[0]) 43 return ans 44 45 46 def get_zdt(name="zdt4"): 47 if name == "zdt4": 48 f_funcs = [zdt4_f1, zdt4_f2] 49 domain = [[0, 1]] 50 for i in range(9): 51 domain.append([-5, 5]) 52 return f_funcs, domain 53 54 if name == "zdt3": 55 f_funcs = [zdt3_f1, zdt3_f2] 56 domain = [[0, 1] for i in range(30)] 57 return f_funcs, domain
1 # 实现zdt.py 2 import numpy as np 3 from nsga2 import * 4 import matplotlib.pyplot as plt 5 from zdt_funcs import * 6 7 8 # 画图 9 def draw(P: object) -> object: 10 for t in P: 11 # 每level 12 x = [p.f[0] for p in P] 13 y = [p.f[1] for p in P] 14 # plt.clf() 15 plt.xlabel("f0") 16 plt.ylabel("f1") 17 plt.scatter(x, y, s=5) # s 点的大小 c 点的颜色 alpha 透明度 18 19 plt.show() 20 21 22 def draw_rank(F): 23 for t in F: 24 # 每level 25 x = [p.f[0] for p in t] 26 y = [p.f[1] for p in t] 27 plt.scatter(x, y, s=15) # s 点的大小 c 点的颜色 alpha 透明度 28 29 plt.show() 30 31 32 # 准备目标问题 33 34 35 f_funcs, domain = get_zdt("zdt3") 36 # 准备参数 37 pop_size = 300 38 dna_size = len(domain) 39 pm = 0.2 40 41 # 开始操作 42 nsga2 = nsga2(pop_size, dna_size, pc=1, pm=0.7 43 , f_funcs=f_funcs, domain=domain) 44 45 # x1 [0,1] xi [-5,5] 46 P = nsga2.ini_pop() 47 # 计算初始适应度 48 nsga2.calculate_pop_fitness(P) 49 # 进行非支配排序 50 F = nsga2.fast_non_dominated_sort(P) 51 # 计算拥挤距离 52 nsga2.crowding_distance_pop(F) 53 R = P 54 55 N = 100 56 for i in range(N): 57 print(i) 58 # 选择 59 P = nsga2.select(R) 60 # 交叉 61 Q = nsga2.pop_cross(P) 62 # 变异 63 Q = nsga2.pop_mutation(Q) 64 # 合并 65 R = P + Q 66 # 计算适应度 67 nsga2.calculate_pop_fitness(R) 68 # 非支配排序 69 F = nsga2.fast_non_dominated_sort(R) 70 # 画个图 71 # draw_rank(F) 72 # 计算拥挤距离 73 nsga2.crowding_distance_pop(F) 74 75 P = nsga2.select(R) 76 # 画图 77 draw(P)
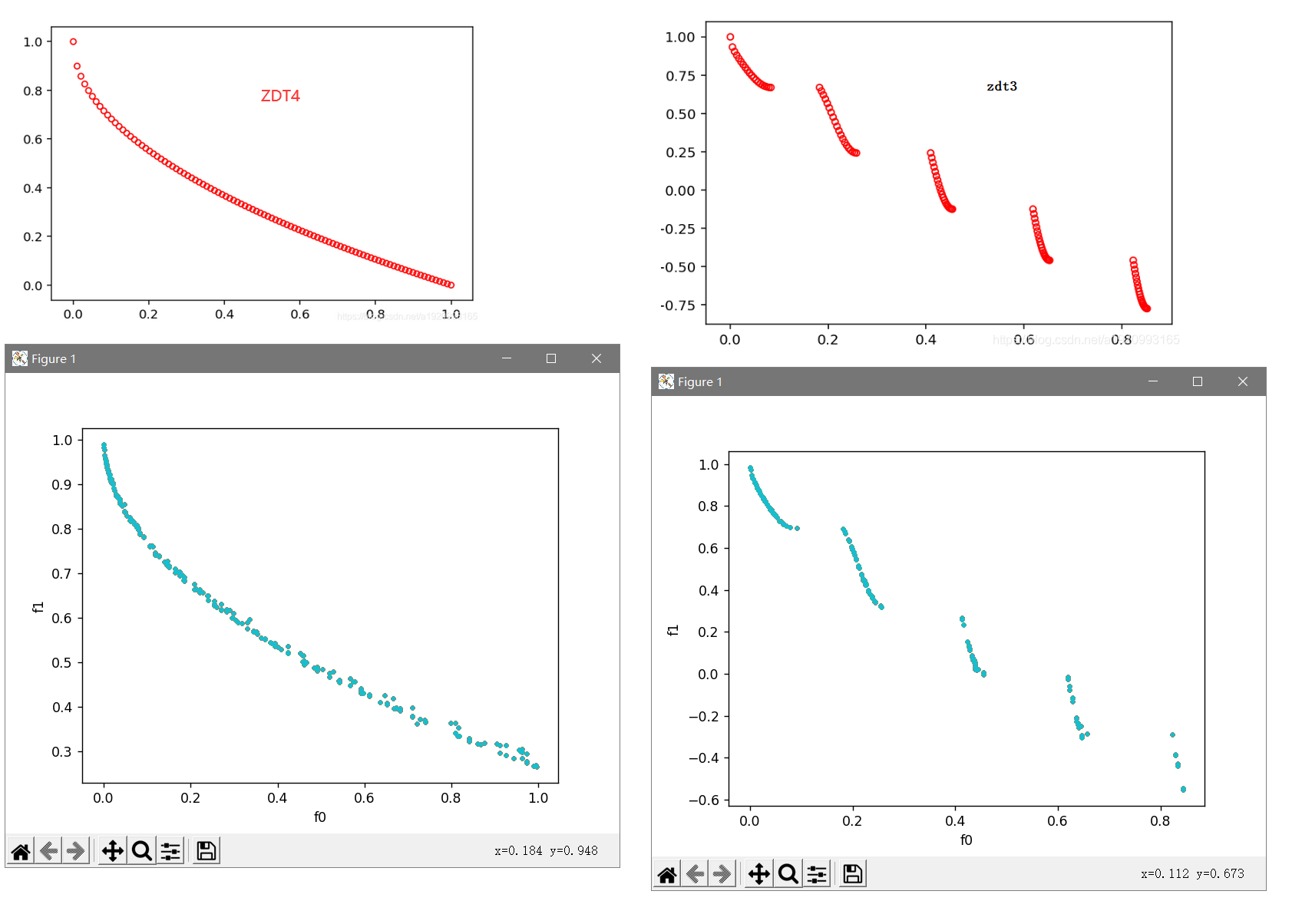
实现效果:
增加种群数量以及迭代次数,能够使曲线更加的完美。我电脑i3 10105f。在代码中参数的配置下,能够很快运行完成。