前言
常用的几何变换中旋转是较为复杂的一种，最近看《Physically Based Rendering, Second Edition: From Theory To Implementation》一书涉及绕任意轴旋转的实现，也给出了大体思路，但具体的推导过程及最后的旋转矩阵并未直接地给出，故根据参考Animated CGEM: Rotation About an Arbitrary Axis总结（欢迎指正）。
（一）基础
1.点乘与叉乘
点乘（dot）亦称作内积或数量积，如图，a·b = |a||b|cosφ
图1：两向量的内积
坐标形式：a = (ax, ay, az) ，b = (bx, by, bz)
a·b = axbx + ayby + azbz
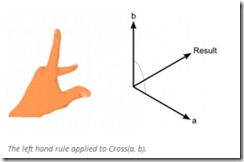
叉乘（cross）亦称作外积，如图，叉乘满足|a x b| = |a||b|sinφ
图2：表示两向量的叉积
图3：左手系示意
由此，叉乘所得向量模为以两叉乘向量为邻边构成的平行四边形的面积大小，叉乘所得的向量与两向量垂直，方向在左手坐标系下依左手定则，pbrt用的是左手系，故手掌与a、b向量构成的平面垂直，除拇指外四指由b转向a，此时拇指的方向即叉乘向量的方向（左手系三个坐标轴亦按上述方法确定）
叉乘的坐标形式：a=(a1,b1,c1)，b=(a2,b2,c2)
a x b = (b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)
2.矩阵
对于线性变换（Linear Transformation），矩阵的三列就是在该变换下的三个坐标轴的反映，如果T是线性变换，M是对应的矩阵，那么矩阵M（4x4）中第一列即把T应用到（1,0,0,）的结果。
在齐次空间（Homogeneous Space）下，M描述一个线性变换，将M作用到坐标系中的x轴向量（1,0,0），恰好得到M的第一列，依次类推第二列即作用到y轴的结果，最后一列表示的是位置相关的信息。
即Mx = M [ 1 0 0 0]T = [m00 m10 m20 m30]T
（二）绕任意轴旋转的推导
直观形象：
图4：绕任意轴旋转的直观形象
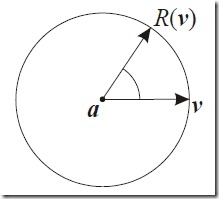
v为被旋转向量，a为给定的任意的旋转轴
容易想象v绕a旋转一周形成一个圆锥，更明确地说，将v沿旋转轴和垂直旋转轴方向分解为两个分向量，平行旋转轴的分向量并不旋转，是垂直分向量在平面内旋转
图5沿正面看 从a的方向往下看
推导：
图6：各向量间的关系
下列推导在a为单位向量的情况下进行，否则得到的是错误的结果
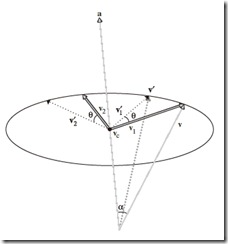
如上图，a是旋转轴，v是被旋转向量，v绕a旋转θ度，旋转平面与a垂直，vc为v沿着a方向分解的分量，v1为v沿着a的垂直方向分解的分量
以a的起点为原点；以a为竖轴；v1为横轴（纵轴）；与v1、a垂直的向量v2为纵轴（横轴）建立坐标系，可以写旋转后得到的结果v’的向量表达式：
v’= vc + v1’
图7：从正面看 俯视
易知：vc = a|v|cosα = (v·a)a
v1 = v - vc
v2 = v1 x a （注意a是单位向量，所以|v2| = |v1|）
v’= vc + v1’
v1’= |v’|cosθ·1/|v1|·v1 + |v’|sinθ·1/|v2|·v2
但由于|v1| = |v2|= |v’|，故消去后得到：v’= vc + v1cosθ + v2sinθ
再整理成矩阵形式，我们将这个矩阵应用到坐标系中，那么就实现了原来点或向量的旋转，最后完成旋转再将坐标系恢复为原坐标系。
令a=（ax, ay, az）， v =（1,0,0）
vc = (ax²，axay, axaz)
v1 = v - vc = (1-ax², -axay, -axaz)
v2 = v1 x a = (0, az, -ay)
代入v’= vc + v1cosθ + v2sinθ得：
令a=（ax, ay, az）， v =（0, 1, 0）；令a=（ax, ay, az）， v =（0, 0, 1）可得到旋转矩阵的第二列、第三列。
最终所得到的即Goldman公式：
