图总结

一、思维导图

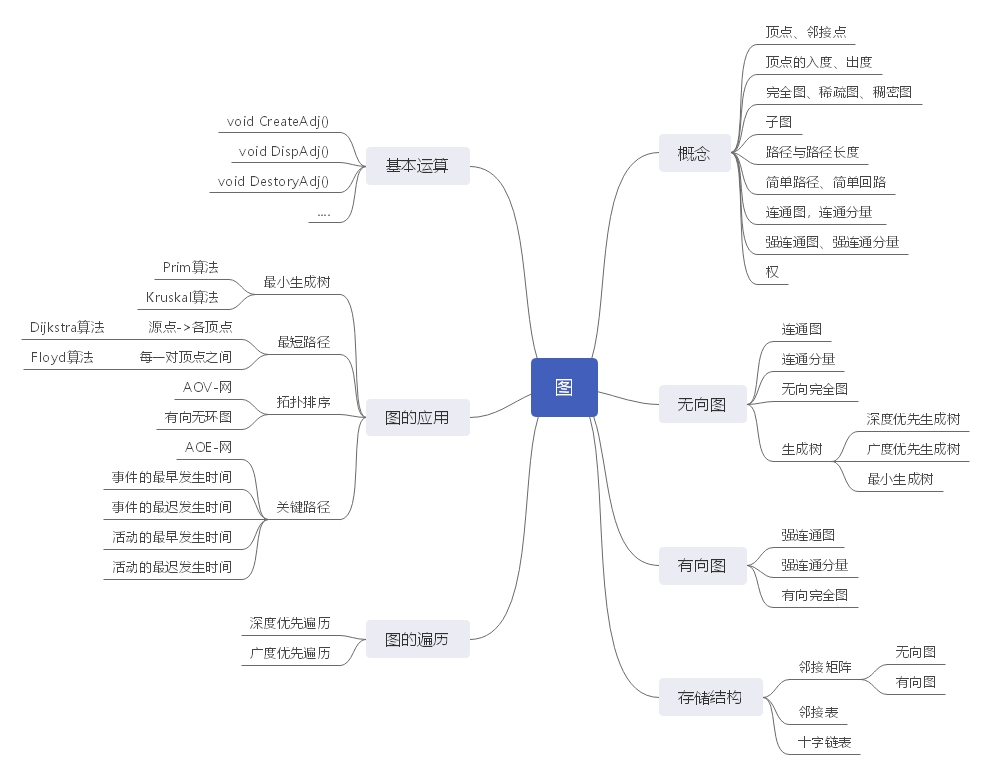
 二、重点笔记

1、图的遍历

(1)深度优先遍历(DFS)

深度优先遍历类似二叉树的前序遍历。简言而知，我们从一个顶点出发，然后一探到底不断深入并访问，直到底后再返回上一级，若还有支路便继续向该支路深入。

例1：

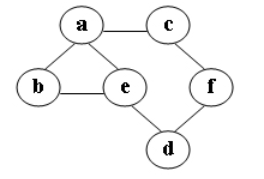
若按照该题进行DFS，从a点出发，a到b，b到e，e到a，发现访问过了返回e，e再到d，d到f，最后到c，所以DFS的结果是a、b、e、d、f、c。

DFS的遍历结果并不一定唯一。以该题为例，可能的结果还有a、c、f、d、e、b。

例2 ：

在邻接表上进行DFS，思路不变，从V1出发，到V3，V3再到V4，死路，返回上一级V3，然后再访问V5，V5再访问V2，死路，回到V5再访问V4，死路，再返回到V1，再访问V2、V4，发现都被访问过了，DFS结束，所以最后DFS的结果是V1、V3、V4、V5、V2。

(2)广度优先遍历(BFS)

广度优先遍历类似二叉树的层序遍历。先遍历离起点最近的邻接点，遍历完这一层再进行起点的邻接点的广度优先遍历。

例1：

 比如说该例为某图的邻接矩阵，我们进行BFS，从第一行开始(从第一行到最后一行分别表示V1~V6)。先访问V1，再访问与V1相连的节点，V2、V3、V5，这一层遍历完了，我们再对V2进行BFS，访问V4，以次类推，最终BFS的结果是V1、V2、V3、V5、V4、V6。

2、最小生成树

(1)Prim算法

 

第一步：取图中任意一顶点v作为生成树的根。
第二步：往生成树上添加心的顶点w，在添加的顶点w和已经在生成树上的顶点v之间必定存在一条边，并且该边的权值在所有连通顶点v和w之间的边中取值最小。
第三步：继续往生成树上添加顶点，直至生成树上含有n个顶点为止。

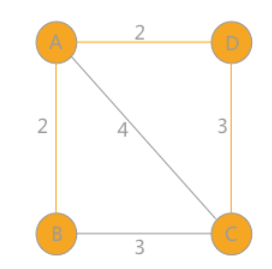
①以下图示例，若从A点出发，此时w选取与A点最近(相连权值最小的顶点)的顶点B

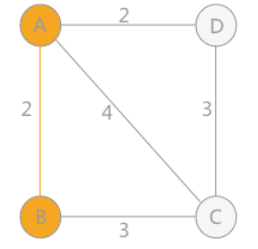
②此时可以看作A、B为一个整体，与这个整体最近的节点选取D

 

 

 

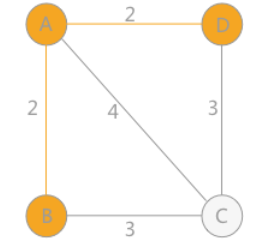
 ③同理，找离此时ABD最近的节点C

 

(2)Kruskal算法

第一步：构造一个只含n个节点的子图SG。
第二步：从权值最小的边开始，若它的添加不使SG中产生回路，则在SG上加上这条边。
第三步：如此重复，直至加上n-1条边为止。

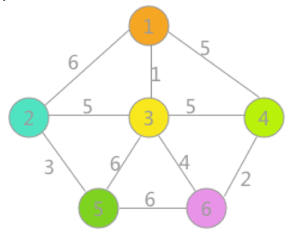
 ①开始时，我们将每一个节点敷上不同的节点，代表还不处于同一个集合

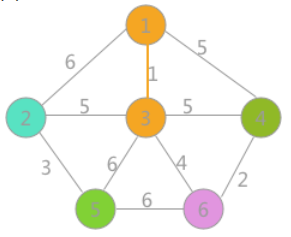
②随后找出权值最小的一，并将其赋上相同的颜色

 

 

③以次类推

 

 

 

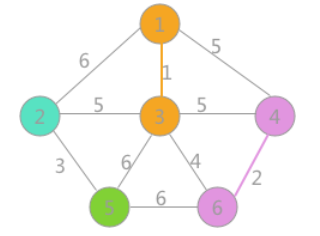
注：再遇见加入某边时候会形成回路时要舍弃这种可能。

3、最短路径

(1)Dijkstra算法

 

Path数组求最短路径

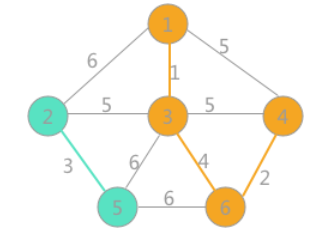
例：

 

 

若要求到1->5的最短路径，我们观察到5的上一个结点是3，3的上一个结点是4，4的上一个节点是1，所以到5的最短路径是1->4->3->5，路径长度为60。

 

(2)Floyd算法