树、二叉树、查找算法总结

一、树

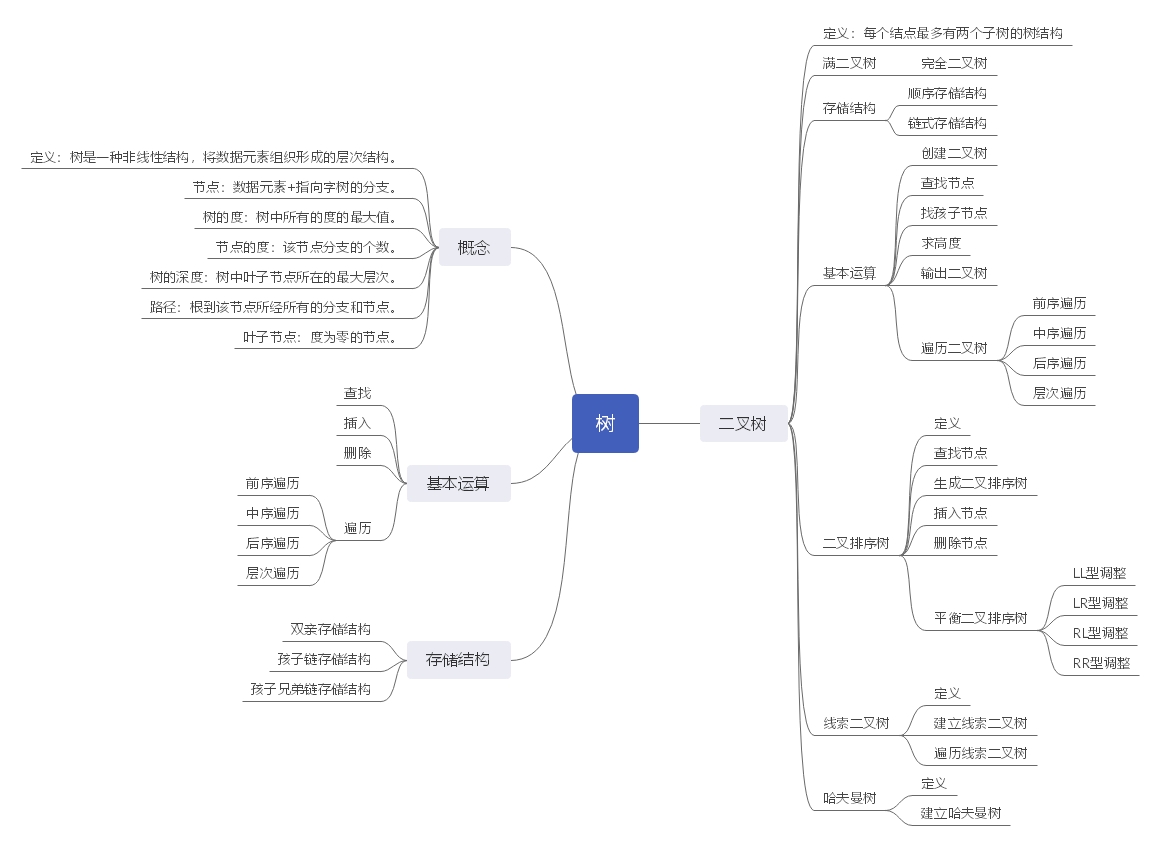
二、二叉树

1、基本性质：

(1)在二叉树的第i层上至多有2^(i-1)个节点。

(2)深度为h的二叉树上至多有2^h-1个节点。

(3)对任何一棵二叉树，若含有n0个叶子节点，n2个度为2的节点，则n0=n2+1。

(4)满二叉树：深度为k且含有2^k-1个节点的二叉树，也叫完美二叉树。

(5)完全二叉树：树中共n个节点，则该n个节点的编号与满二叉树中的节点编号一一对应。

2、链式存储结构的结构类型定义：

typedef struct node {
    Elemtype data;
    struct* lchild, * rchild;
}BTNode;

 

3、四种遍历

Status PreOrderTraverse(BiTree T)//先序遍历
{
    if (T != NULL) {
        cout << T->data << " ";
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
    return OK;
}

Status InOrderTraverse(BiTree T)//中序遍历
{
    if (T != NULL) {
        InOrderTraverse(T->lchild);
        cout << T->data << " ";
        InOrderTraverse(T->rchild);
    }
    return OK;
}

Status PostOrderTraverse(BiTree T)//后序遍历
{
    if (T != NULL) {
        PostOrderTraverse(T->lchild);
        PostOrderTraverse(T->rchild);
        cout << T->data << " ";
    }
    return OK;
}

Status LevelOrderTraverse(BiTree T)//层次遍历
{
    queue<BiTree> q;
    BiTree front;
    if (T == NULL)
        return ERROR;
    q.push(T);
    while (!q.empty()) {
        front = q.front();
        q.pop();

        if (front->lchild)
            q.push(front->lchild);
        if (front->rchild)
            q.push(front->rchild);
        if (q.size()==0)
            cout << front->data;
        else
            cout << front->data << " ";
    }
    return OK;
}

5、求树高

int GetTreeDepth(BiTree T)
{
    int depth = 0;
    if (!T)
        depth = 0;
    else {
        int ldepth = GetTreeDepth(T->lchild);
        int rdepth = GetTreeDepth(T->rchild);
        depth = 1+(ldepth > rdepth ? ldepth : rdepth);
    }
    return depth;
}

 6、构造二叉树

先序序列+中序序列——可以确定

后序序列+中序序列——可以确定

先序序列+后序序列——不可确定

即需要知道中序序列并且知道前序序列及后序序列之一边可以确认二叉树。

三、线索二叉树

1、结构类型定义

typedef struct node {
    Elemtype data;
    int ltag, rtag;
    struct node* lchild, * rchild;
}TBTNode;

其中ltag和rtag等于0时表示该节点具有左孩子节点和右孩子结点，当ltag和rtag为1时表示该节点的孩子节点指向前驱和后继节点。

2、建立线索二叉树(中序)

TBTNode* pre;//全局变量
TBTNode* CreateThread(TBTNode* b)
{
    TBTNode* root;
    root = new TNTNode;
    root->ltag = 0; root->rtag = 1;
    root->rchild = b;
    if (b == NULL)
        root->lchild = root;
    else {
        root->lchild = b;
        pre = root;
        Thread(b);
        pre->rchild = root;
        pre->rtag = 1;
        root->rchild = pre;
        return root;
    }
}
void Thread(TBTNode*& p)
{
    if (p != NULL) {
        Thread(p->lchild);
        if (p->lchild == NULL) {
            p->lchild = pre;
            p->ltag = 1;
        }
        else
            p->ltag = 0;
        if (pre->rchild == NULL) {
            pre->rchild = p;
            pre->rtag = 1;
        }
        else
            pre->rtag = 0;
        pre = p;
        Thread(p->rchild);
    }
}

 3、遍历线索二叉树

void ThInOrder(TBTNode* tb)
{
    TBTNode* p = tb->lchild;
    while (p != tb) {
        while (p->ltag == 0)
            p = p->lchild;
        cout << p->data;
        while (p->rtag == 1 && p->rchild != tb) {
            p = p->rchild;
            cout << p->data;
        }
        p = p->lchild;
    }
}

四、哈夫曼树

1、特点

(1)只有度为0和度为2的节点。

(2)因为二叉树中n2=n0-1，哈夫曼树共有2n-1个节点，其中n为叶子节点n0。

2、类型定义

 

typedef struct node {
    char data;
    double weight;
    int parent;
    int lchild, rchild;
}HTNode;

 

3、生成哈夫曼树

void CreateHF(HTNode ht[], int n, double weight[], char data[])
{
    int i, j, k, lnode, rnode;
    double min1, min2;
    for (i = 0; i < n; i++) {
        ht[i].parent = ht[i].lchild = ht[i].rchild = -1;
        ht[i].weight = weight[i];
        ht[i].data = data[i];
    }
    for (i = n; i < 2 * n - 1; i++) {
        min1 = min2 = 32767;
        lnode = rnode = -1;
        for (k = 0; k <= i - 1; k++) {
            if (ht[k].parent == -1) {
                if (ht[k].weight < min1) {
                    min2 = min1; rnode = lnode;
                    min1 = ht[k].weight; lnode = k;
                }
            }
            else if (ht[k].weight < min2) {
                min2 = ht[k].weight;
                rnode = k;
            }
        }
    }
}

五、二叉排序树

见上一次互评作业：https://www.cnblogs.com/Tvoimvyan/p/12731391.html

六、树、二叉树和森林

1、森林转二叉树

 

 

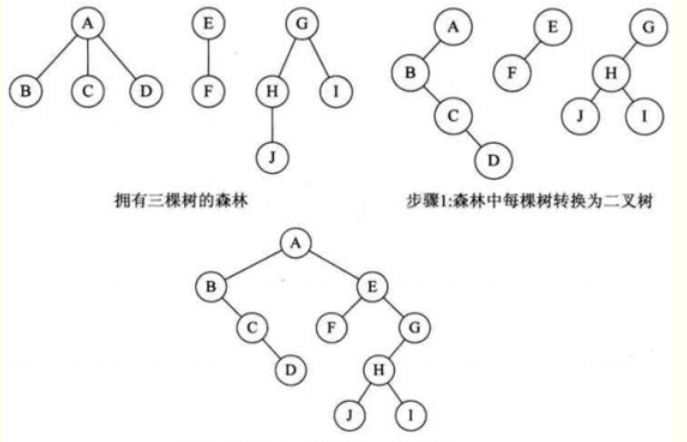
2、树转二叉树

 

 

 3、二叉树转树

 

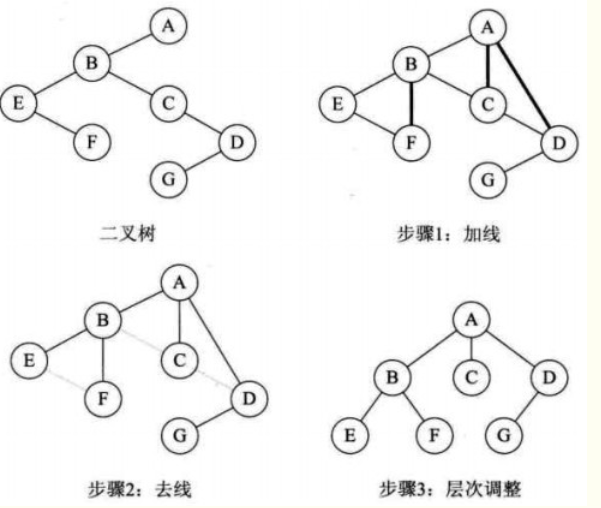
4、二叉树转换为森林

 

 

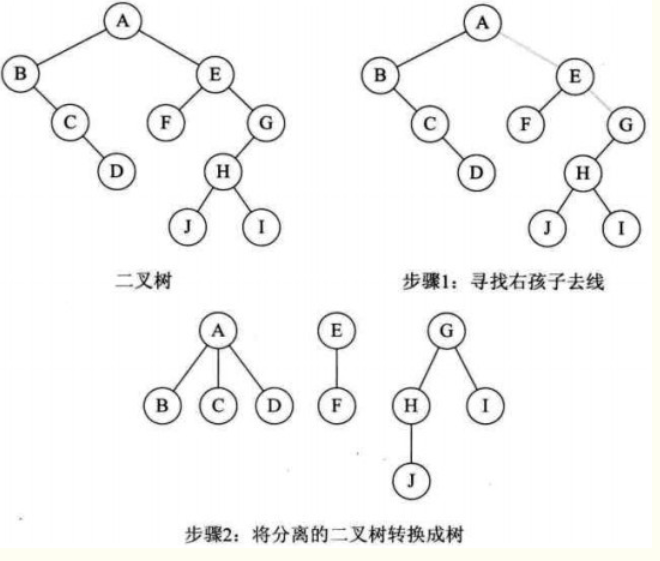
上述总结来自：http://www.cnblogs.com/zhuyf87/archive/2012/11/04/2753950.html

 七、平衡二叉树

调整：

(1)LL型

 

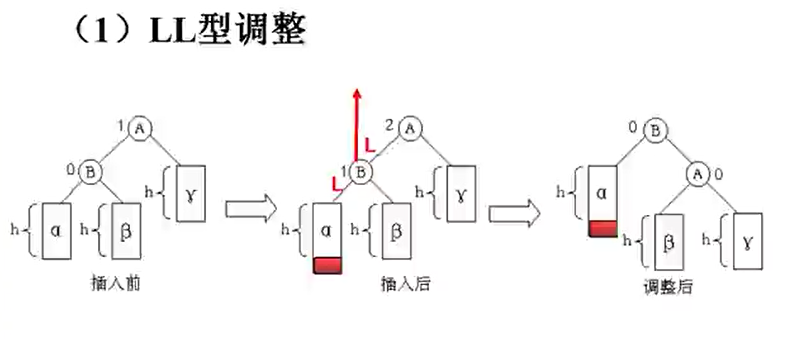
(2)RR型

 

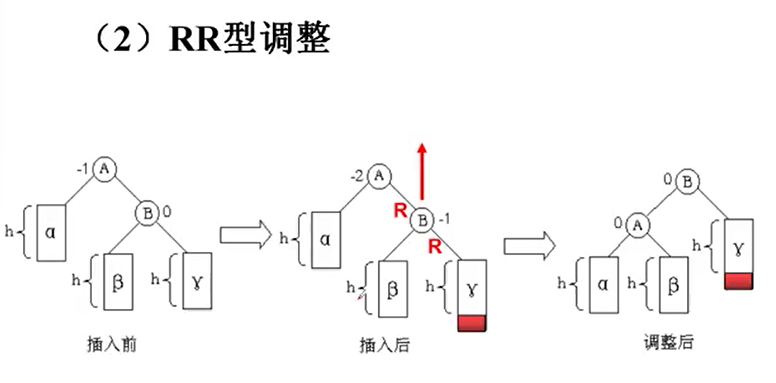
(3)LR型

(4)RL型

 

 

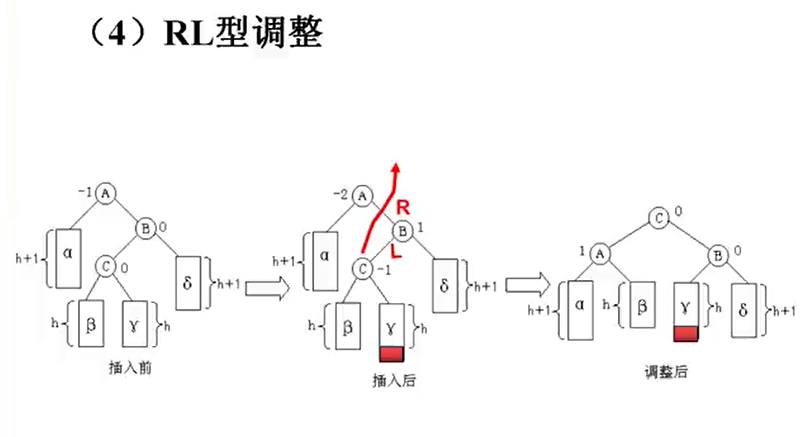
 八、查找

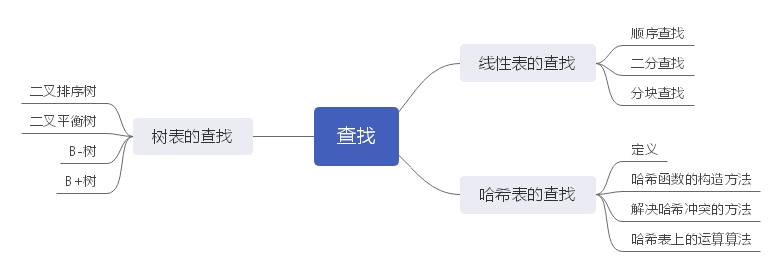
1、平均查找长度(ASL)：需要执行的平均比较次数称为平均查找长度，用以衡量一个查找算法效率优劣。

2、顺序查找(顺序表为例)

int SeqSearch(SeqList R, int n, KeyType k)
{
    int i = 0;
    while (i < n && R[i].key != k)
        i++;
    if (i >= n)
        return 0;
    else
        return i + 1;
}

 

 

ASL计算为(n+1)/2；即查找成功时的ASL约为表厂的一半；查找失败时的ASL为n。

3、二分查找

二分查找要求线性表中的节点必须已按关键字值的递增或递减顺序排列。

int BinSearch(SeqList R, int n, KeyType k)
{
    int low = 0, high = n - 1, mid;
    while (low <= high) {
        mid = (low + high) / 2;
        if (R[mid].key == k)
            return mid + 1;
        if (R[mid].key > k)
            high = mid - 1;
        else
            low = mid + 1;
    }
    return 0;
}

ASL计算约为log2(n+1)-1。

4、分块查找

方法描述：将n个数据元素"按块有序"划分为m块（m ≤ n）。每一块中的结点不必有序，但块与块之间必须"按块有序"；即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，……。

 

操作步骤：

 

①先选取各块中的最大关键字构成一个索引表；

 

②查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；

 

然后，在已确定的块中用顺序法进行查找。

5、B-树

 

(1)定义：①B-树是二叉排序树。②每个节点至多m个孩子节点(至多有m-1个关键字)。③除根节点外，其他节点至少有m/2个孩子节点(即 至少有m/2-1个关键字)。④若根节点不是叶子节点，根节点至少两个孩子节点。

(2)B-树的查找：

①若k=key[i]，则查找成功。

②若k＜key[1]， 则沿着指针ptr[0]所指的子树继续查找。

③若key[i]＜k＜key[i+1]， 则沿着指针ptr[i]所指的子树继续查找。

④若k＞key[n]， 则沿着指针ptr[n]所指的子树继续查找。

⑤查找到某个叶结点，若相应指针为空 ，落入一个外部结点，表示查找失败。

(3)B-树的插入：

参考：https://blog.csdn.net/li_canhui/article/details/85305147

(4)B-树的删除：

参考：https://mp.weixin.qq.com/s?__biz=MjM5MzA1Mzc3Nw==&mid=2247484674&idx=1&sn=8f908ee565531ff7a5c1a481466f3e86&chksm=a69da83c91ea212a44146e21ce147d0815651a4ccffd4ac3834b0420f4cd64e35b74328ed313&token=648694665&lang=zh_CN&utm_medium=hao.caibaojian.com&utm_source=hao.caibaojian.com