数据结构、算法及线性表总结

一、数据结构

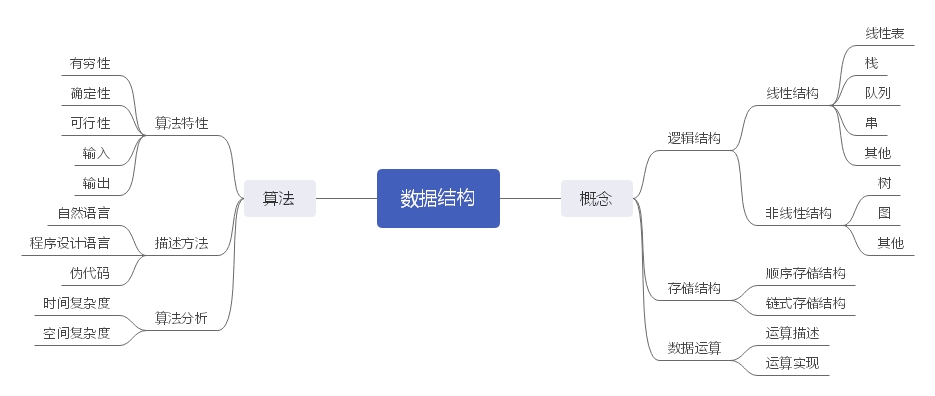
1、数据结构的概念

　　数据结构是相互之间存在一种或多种特定关系的数据元素的集合。数据由数据元素组成，数据元素由数据项组成，数据元素是数据的基本单位，数据项是数据的最小单位。

2、逻辑结构

　　数据的逻辑结构分为线性结构和非线性结构，其中线性结构包括线性表、栈、队列和串等，非线性结构包括树形结构和图形结构等。

3、存储结构

　　数据的存储结构分为顺序存储结构和链式存储结构。顺序存储结构是逻辑上相邻存储在物理位置上相邻的存储单元如数组；链式存储结构不要求逻辑相连的节点在物理位置上也相邻，其中可借用指针来表示数据之间的逻辑关系。

4、算法

　　(1)算法的五个特征包括有穷性、确定性、可行性、输入以及输出。

　　(2)算法的描述方法可以从自然语言、程序设计语言和伪代码入手。其中自然语言描述能力最强，但是撰写起来复杂；程序设计语言可读性最差但是撰写方便；伪代码综合前两者的优点，在进行代码编写过程中应用较多。

　　(3)算法可以从时间复杂度和空间复杂度来分析算法的效率：衡量算法效率的方法还包括事后统计法和事前分析估算法。

　　　　①时间复杂度：算法中基本运算执行次数T(n)是问题规模n的某个函数记作T(n)=O(f(n))。常出现常数阶O(1)、线性阶O(n)、平方阶O(n^2)、对数阶O(log2n)；计算时间复杂度只需求出T(n)的最高阶，忽略其低阶和常数阶，由此可以看出当问题规模n较大时算法的时间效率。

　　　　②空间复杂度：算法在运行过程中临时占用的存储空间的度量。

　　　　一般情况下，运算的空间较为充足，常以算法的空间复杂度作为算法优劣的衡量指标。

5、数据类型与数据结构：

　　抽象数据类型(ADT)框架：

　　数据类型名称 {

　　　　数据对象；

　　　　数据关系；

　　　　基本操作；

　　}

 二、线性表

1、顺序表

#define Maxsize 50
typedef int Elemtype;
typedef struct {
    Elemtype data[Maxsize];
    int length;
} SqList;

特点：①逻辑上相邻<->物理地址上相邻；②随机存储(访问时更加快速)。

优点：①相对用满时空间利用率高(不用像链表一样还要分配内存给指针)；②读取速度快，随机存储的优异性。

缺点：①若事先不知道空间要分配内存的多少将会浪费很多内存空间或者空间不足导致溢出；②插入和删除的操作较慢。

(1)插入元素

 

bool InsertList(SqList*& L, int i, Elemtype e)
{
    if (i < 1 || L->length + 1)
        return false;
    i--;
    for (int j = L->length; j > i; j--)
        L->data[j] = L->data[j - 1];
    L->data[i] = e;
    L->length++;
    return true；
}

时间复杂度：O(L->length)。

(2)删除元素

bool DeleteList(SqList*& L, int i, Elemtype &e)
{
    if (i < 1 || i->length + 1)
        return false;
    i--;
    e = L->data[i];
    for (int j = i; j < L->length-1; j++)
        L->data[j] = L->data[j + 1];
    L->length--;
    return true;
}

时间复杂度：O(L->length)。

2、链表

typedef struct LNode {
    Elemtype data;
    struct LNode* next;
}LinkList;

特点：线性表中的数据元素存放在一组地址任意的存储节点，存储之间用next连接。

优点：①动态分配内存；②删除和插入操作过程不用移动表中元素的位置。

缺点：①相比顺序存储结构访问元素相对较慢；②需要分配空间给指向下一节点的指针。

节点构成：数据元素+指针；其中数据元素存放该节点的数据值，指针存放该节点的下一个节点的地址。

(1)求表中指定位置的数据元素

 

bool GetElem(LinkList* L, int i, Elemtype& e)
{
    int j = 0;
    LinkList* p = L;
    while (j < i && p != NULL) {
        j++;
        p = p->next;
    }
    if (p == NULL)
        return false;
    else {
        e = p->data;
        return true;
    }
}

时间复杂度：O(L->length)

(2)插入元素

bool InsertList(LinkList*& L, int i, Elemtype e)
{
    int j = 0;
    LinkList* p = L;
    while (j < i - 1 && p != NULL) {
        j++;
        p = p->next;
    }
    if (p == NULL)
        return false;
    else {
        s = new LNode;
        s->data = e;
        s->next = p->next;
        p->next = s;
    }
}

时间复杂度：O(L->length)。

(3)删除元素

bool DeleteList(LinkList*& L, int i, Elemtype e)
{
    int j = 0;
    LinkList* p = L, * q;
    while (j < i - 1 && p != NULL) {
        j++;
        p = p->next;
    }
    if (p == NULL)
        return false;
    else {
        q = p->next;
        if (q == NULL)
            return false;
        e = q->data;
        p->next = q->next;
        delete p;
        return true;
    }
}

时间复杂度：O(L->length)。

(4)建单链表-头插法

void CreateListF(LinkList*& L, Elemtype a[], int n)
{
    LinkList* s;
    L = new LNode;
    L->next = NULL;
    for (int i = 0; i < n; i++) {
        s = new LNode;
        s->data = a[i];
        s->next = L->next;
        L->next = s;
    }
}

输出的结果与输入相反。

(5)建单链表-尾插法

void CreateListR(LinkList*& L, Elemtype a[], int n)
{
    LinkList* s, * r;
    L = new LNode;
    r = L;
    for (int i = 0; i < n; i++) {
        s = new LNode;
        s->data = a[i];
        r->next = s;
        r = s;
    }
    r->next = NULL;
}

输出的结果与输入相同。

3、双链表

 

typedef struct DNode {
    Elemtype data;
    struct DNode* prior;
    struct DNode* next;
}DLinkList;

 

(1)节点插入

s->next = p->next;
p->next = s;
s->next->prior = s;
s->prior = p;

(2)节点删除

q = p->next;
p->next = q->next;
q->next->prior = p;
delete q

 4、有序表：其中所有元素以递增或递减的方式有序排列

(1)插入

//顺序表
void ListInsert(SqList*& L, Elemtype e)
{
    int i = 0, j;
    while (i < L->length && L->data[i] < e)
        i++;
    for (j = L->length; j > i; j--)
        L->data[j] = L->data[j - 1];
    L->data[i] = e;
    L->length++;
}

//链式表
void ListInsert(LinkList*& L, Elemtype e)
{
    LinkList* pre = L, * p;
    while (pre->next != NULL && pre->next->data < e)
        pre = pre->next;
    p = new LNode;
    p->data = e;
    p->next = pre->next;
    pre->next = p;
}

三、栈

1、栈

　　概念：栈是限制仅在线性表的一端进行插入与删除操作的线性表

　　特点：后进先出(LIFO)

2、顺序栈

#define Maxsize 100
typedef struct {
    Elemtype data[Maxsize];
    int top;
}SqStack;

(1)进栈

bool Push(SqStack*& s, ELemtype e)
{
    if (s->top == Maxsize - 1)
        return false;
    s->top++;
    s->data[s->top] = e;
    return true;
}

(2)出栈

bool Pop(SqStack*& s, Elemtype& e)
{
    if (s->top == -1)
        return false;
    e = s->data[s->top];
    s->top--;
    return true;
}

(3)取栈顶元素

bool GetTop(SqStack* s, Elemtype& e)
{
    if (s->top == -1)
        return false;
    e = s->data[s->top];
    return true;
}

3、链式栈

typedef struct linknode {
    Elemtype data;
    struct linknode* next;    
}LiStack;

(1)进栈

void Push(LiStack*& s, Elemtype e)
{
    LiStack* p;
    p = new LiStack;
    p->data = e;
    p->next = s->next;
    s->next = p;
}

(2)出栈

void Pop(LiStack*& s, Elemtype& e)
{
    LiStack* p;
    if (s->next == NULL)
        return false;
    p = s->next;
    e = p->data;
    s->next = p->next;
    delete p;
    return true;
}

(3)取栈顶元素

void GetTop(LiStack* s, Elemtype& e)
{
    if (s->next == NULL)
        return false;
    e = s->next->data;
    return true;
}

4、#include<stack>

stack

stack模板类的定义在<stack>头文件中。

stack模板类需要两个模板参数，一个是元素类型，一个容器类型，但只有元素类型是必要的，在不指定容器类型时，默认的容器类型为deque。

定义stack对象的示例代码如下：

stack<int> s1;
stack<string> s2;

stack的基本操作有：

入栈，如例：s1.push(x);

出栈，如例：s1.pop();注意，出栈操作只是删除栈顶元素，并不返回该元素。

访问栈顶，如例：s1.top()

判断栈空，如例：s1.empty()，当栈空时，返回true。

访问栈中的元素个数，如例：s1.size()

四、队列

1、队列

　　概念：只允许在表的一端(队尾)进行插入，而在表的另一端(队头)进行删除。

　　特点：先进先出(FIFO)。

2、顺序队列

#define MaxSize 100
typedef struct {
    Elemtype data[Maxsize];
    int front;
    int rear;
}SqQu

(1)入队

bool enQueue(SeCiQueue*& q, Elemtype e)
{
    if ((q->rear+1)%Maxsize==q->front)
        return false;
    q->rear = (q->rear + 1) % Maxsize;
    q->data[q->rear] = e;
    return true;
}

(2)出队

bool deQueue(SeciQueue*& q, Elemtype& e)
{
    if (QueueEmpty(q))
        return false;
    q->front = (q->front + 1) % Maxsize;
    e = q->data[q->front];
    return true;
}

3、链式队伍

typedef struct QNode {
    Elemtype data;
    struct QNode* next;
}QNode;

 

(1)入队

void enQueue(LiQueue*& q, Elemtype e)
{
    QNode* newNode = new QNode;
    newNode->data = e;
    newNode->next = NULL;
    if (QueueEmpty(q)) {
        q->rear = newNode;
        q->front = newNode;
    }
    else {
        q->rear->next = newNode;
        q->rear = newNode;
    }
}

(2)出队

bool deQueue(LiQueue*& q, Elemtype& e)
{
    QNode* del;
    if (QueueEmpty(q))
        return false;
    del = q->front;
    if (q->front = q->rear)
        q = front = q->rear = NULL;
    else
        q->front = q->front->next;
    e = del->data;
    delete del;
    return true;
}

4、#include<queue>

queue

queue模板类的定义在<queue>头文件中。

与stack模板类很相似，queue模板类也需要两个模板参数，一个是元素类型，一个容器类型，元素类型是必要的，容器类型是可选的，默认为deque类型。

定义queue对象的示例代码如下：

queue<int> q1;
queue<double> q2;

queue的基本操作有：

入队，如例：q1.push(x); 将x接到队列的末端。
出队，如例：q1.pop(); 弹出队列的第一个元素，注意，并不会返回被弹出元素的值。
访问队首元素，如例：q1.front()，即最早被压入队列的元素。
访问队尾元素，如例：q1.back()，即最后被压入队列的元素。
判断队列空，如例：q1.empty()，当队列空时，返回true。
访问队列中的元素个数，如例：q1.size()

五、串

1、串

　　概念：由零个或多个字符组成的有限序列。

2、#include<string>

　　详情访帖：http://blog.sina.com.cn/s/blog_453a02280100r8tv.html

3、BF算法

 

1.在串S和串T中设置比较的起始下标i=0，j=0
2.重复下述操作，直到S或T的所有字符比较完毕
    ①如果S[i]=T[j]，则继续比较S和T的下一对字符
    ②否则，回溯下标i=i-j+1，j=0
3.如果T中所有字符比较完毕，则返回匹配的开始位置
    i-t.length(t为T字串)；否则返回-1
时间复杂度：O(n*m)

4、KMP算法

1.在串S和串T中，分别设置比较的起始下标，i=0，j=0
2.重复下述操作，直到S或T的所有字符均比较完毕
    ①如果S[i]等于T[j]，则继续比较S和T的下一对字符
    ②否则，将下标j回溯到next[j]位置，即j=next[j]
    ③如果j=-1，则将下标i和j分别加1，准备下一趟比较
3.如果T中所有字符均比较完毕，则返回本趟匹配的开始位置，否则返回-1

六、总结

1、在这次总结中，巩固了几种线性表的基本操作，对数据结构中结构部分有了更深的了解。

2、因为总结的时间没有把握好，写的仍不是很具体，有些操作还没有彻底理解。

3、在实际操作中仍不熟练，之后会加深代码的应用，增加熟练度。