AVL树
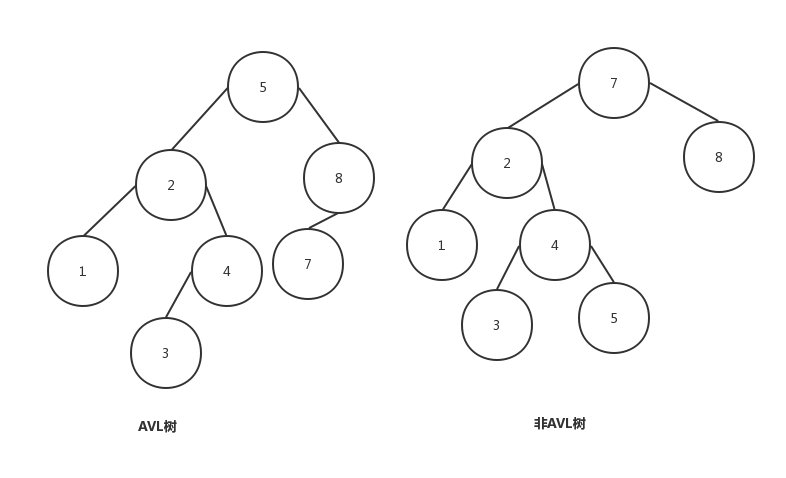
AVL(Adelson-Velskii和Landis)树是带有平衡条件(balance condition)的二叉查找树。这个平衡条件必须要容易保持,而且它保证树的深度须是O(\(log{N}\))。最简单的想法是要求左右子树具有相同的高度。
另一个平衡条件是要求每个节点都必须有相同高度的左子树和右子树。如果空子树的高度定义为-1(通常就是这么定义),那么只有具有2k-1个节点的理想平衡树(perfectly balanced tree)满足这个条件。一颗AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树。
旋转
左左单旋转
从下图可以看出,结点X并不能满足AVL树的性质,因为它的左子树比右子树深2层,这种情况就是典型的LL情景,此时需要通过右向旋转来修复失衡的树,如图1,X经过右旋转后变成图2,W变为根结点,X变为W的右子树,同时W的右子树变为X的左子树,树又重新回到平衡,各个结点的子树高度差都已在正常范围。一般情况下,我们把X结点称为失衡点,修复一棵被破坏的AVL树时,找到失衡点是很重要的并把通过一次旋转即可修复平衡的操作叫做单旋转,从图3和图4可知,在原始AVL树插入7结点后,结点9变为失衡点,树再满足AVL性质,因此需要对9结点进行左左单旋转(即向右旋转)后,得到图4,我们发现此时并没有操作树的根结点(6),实际上这是因为正常情况下,不必从树的根结点进行旋转,而是从插入结点处开始,向上遍历树,并更新和修复在这个路径上的每个结点的平衡及其平衡信息(高度)即可。

/**
* 左左单旋转(LL旋转) w变为x的根结点, x变为w的右子树
* @param x
* @return
*/
private AVLNode<T> singleRotateLeft(AVLNode<T> x){
//把w结点旋转为根结点
AVLNode<T> w= x.left;
//同时w的右子树变为x的左子树
x.left=w.right;
//x变为w的右子树
w.right=x;
//重新计算x/w的高度
x.height=Math.max(height(x.left),height(x.right))+1;
w.height=Math.max(height(w.left),x.height)+1;
return w;//返回新的根结点
}
右右单旋转
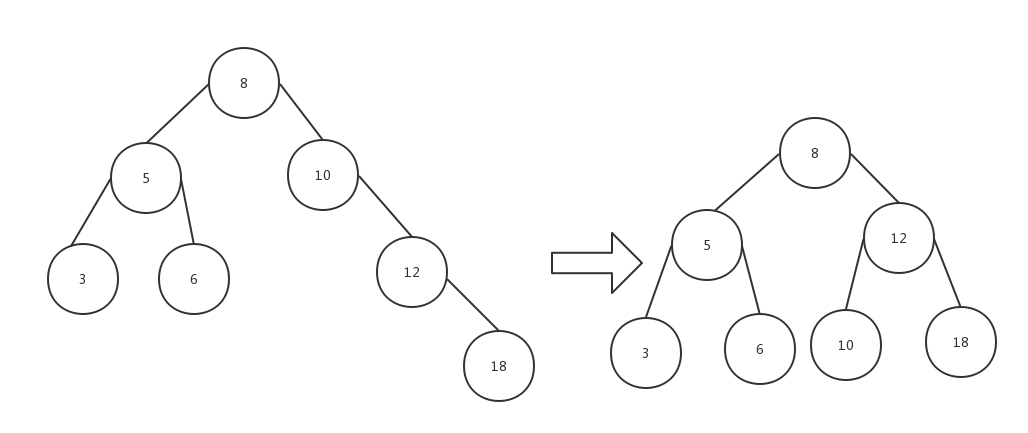
接着再来看看右右单旋转(RR)的情景,如下图,可以发现与左左单旋转的情况恰好是一种镜像关系,同样结点X并不能满足AVL树的性质,在这样的情景下,需要对X结点进行左旋转来修复树的平衡,如图1经左旋转后变了图2,此时X变为了根结点,W变为X的左孩子,X的左子树变为W的右子树,而树又重新恢复了平衡。如图3和图4的实例情景,原始的AVL树在12处插入结点18后,结点10就变成了失衡点,因为10的左子树和右子树的高度相差2,显然不符合AVL树性质,需要对结点10进行右右单旋转修复(向左旋转),然后得到图4,此时树重新回到了平衡,这便是右右单旋转(RR)的修复情景。
/**
* 右右单旋转(RR旋转) x变为w的根结点, w变为x的左子树
* @return
*/
private AVLNode<T> singleRotateRight(AVLNode<T> w){
AVLNode<T> x=w.right;
w.right=x.left;
x.left=w;
//重新计算x/w的高度
w.height=Math.max(height(w.left),height(w.right))+1;
x.height=Math.max(height(x.left),w.height)+1;
//返回新的根结点
return x;
}
左右双旋转
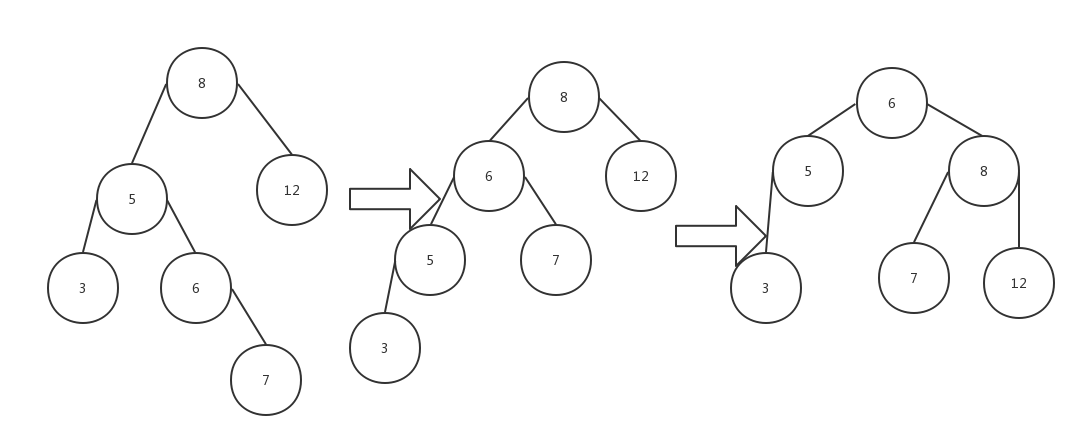
为了重新平衡,通过上述的分析显然不能把X根结点,而X与W间的旋转也解决不了问题,那唯一的旋转就是把Y作为新根。这样的话,X、W就不得不成为Y的孩子结点,其中W作为Y的左孩子结点,而X成为Y的右孩子结点。这里我们以下图为例来分析,为了达到以上结果,需要W、Y进行单旋转(图1),这里我们可把WY组成的子树看成前面的右右旋转情景,然后进行左向旋转,得到图2,W变为Y的左子树同时Y的左子树B变成W的右子树,其他不变,到此第一次旋转完成,进行第二次旋转,以X结点向右进行旋转(同样可看作左左情景),由图2得到图3,X变成Y的右孩子结点并且Y的右子树C变成X的左子树,第二次旋转完成,树也重新恢复到平衡。
/**
* 左右旋转(LR旋转) x(根) w y 结点 把y变成根结点
* @return
*/
private AVLNode<T> doubleRotateWithLeft(AVLNode<T> x){
//w先进行RR旋转
x.left=singleRotateRight(x.left);
//再进行x的LL旋转
return singleRotateLeft(x);
}
右左双旋转

/**
* 右左旋转(RL旋转)
* @param w
* @return
*/
private AVLNode<T> doubleRotateWithRight(AVLNode<T> x){
//先进行LL旋转
x.right=singleRotateLeft(x.right);
//再进行RR旋转
return singleRotateRight(x);
}
实现
public class AVLTree<T extends Comparable<T>> {
private AVLTreeNode<T> mRoot; // 根结点
// AVL树的节点(内部类)
class AVLTreeNode<T extends Comparable<T>> {
T element; // 值
int height; // 高度
AVLTreeNode<T> left; // 左孩子
AVLTreeNode<T> right; // 右孩子
public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) {
this.element = key;
this.left = left;
this.right = right;
this.height = 0;
}
}
/*
* 获取树的高度
*/
private int height(AVLTreeNode<T> tree) {
if (tree != null)
return tree.height;
return 0;
}
public int height() {
return height(mRoot);
}
/*
* LL:左左对应的情况(左单旋转)。
*
* 返回值:旋转后的根节点
*/
/**
* LL:左左对应的情况(左单旋转)。
*
* @param k2
* @return 旋转后的根节点
*/
private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) {
AVLTreeNode<T> k1;
k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1;
}
/**
* 右右对应的情况(右单旋转)。
*
* @param k1
* @return 旋转后的根节点
*/
private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) {
AVLTreeNode<T> k2;
k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
k2.height = Math.max(height(k2.right), k1.height) + 1;
return k2;
}
/**
* LR:左右对应的情况(左双旋转)。
*
* @param k3
* @return 旋转后的根节点
*/
private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) {
k3.left = rightRightRotation(k3.left);
return leftLeftRotation(k3);
}
/**
* RL:右左对应的情况(右双旋转)。
*
* @param k1
* @return 旋转后的根节点
*/
private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}
public void insert(T key) {
mRoot = insert(mRoot, key);
}
/**
* 将结点插入到AVL树中,并返回根节点
*
* @param tree AVL树的根结点
* @param key 插入的结点的键值
* @return 根节点
*/
private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) {
if (tree == null) {
// 新建节点
return tree = new AVLTreeNode<T>(key, null, null);
}
int cmp = key.compareTo(tree.element);
if (cmp < 0) {// 将key插入到"tree的左子树"的情况
tree.left = insert(tree.left, key);
} else if (cmp > 0) { // 将key插入到"tree的右子树"的情况
tree.right = insert(tree.right, key);
}
return balance(tree);
}
private static final int ALLOWED_IMBALANCE = 1;
private AVLTreeNode<T> balance(AVLTreeNode<T> tree) {
if (tree == null) {
return tree;
}
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.left) - height(tree.right) > ALLOWED_IMBALANCE) {
if (height(tree.left.left) >= height(tree.left.right)) {
leftLeftRotation(tree);
} else {
leftRightRotation(tree);
}
} else if (height(tree.right) - height(tree.left) > ALLOWED_IMBALANCE) {
if (height(tree.right.right) >= height(tree.right.left)) {
rightRightRotation(tree);
} else {
rightLeftRotation(tree);
}
}
tree.height = Math.max(height(tree.left), height(tree.right)) + 1;
return tree;
}
public void remove(T key) {
AVLTreeNode<T> z;
if ((z = search(mRoot, key)) != null)
mRoot = remove(mRoot, z);
}
/*
* (递归实现)查找"AVL树x"中键值为key的节点
*/
private AVLTreeNode<T> search(AVLTreeNode<T> x, T key) {
if (x == null)
return x;
int cmp = key.compareTo(x.element);
if (cmp < 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
}
public AVLTreeNode<T> search(T key) {
return search(mRoot, key);
}
/**
* 删除结点(z),返回根节点
*
* @param tree AVL树的根结点
* @param z 待删除的结点
* @return 根节点
*/
private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) {
if (tree == null)
return tree;
int cmp = z.element.compareTo(tree.element);
if (cmp > 0) {
tree.right = remove(tree.right, z);
} else if (cmp < 0) {
tree.left = remove(tree.left, z);
} else if (tree.left != null && tree.right != null) {
tree.element = findMin(tree.right).element;
tree.right = remove(tree.element, tree.right);
} else {
tree = (tree.left != null) ? tree.left : tree.right;
}
return balance(tree);
}
private AVLTreeNode<T> findMin(AVLTreeNode<T> node) {
if (node != null) {
while (node.left != null) {
node = node.left;
}
}
return node;
}
public AVLTreeNode<T> remove(T t, AVLTreeNode<T> node) {
if (node == null) {
return node;
}
int compareResult = t.compareTo(node.element);
if (compareResult > 0) {
node.right = remove(t, node.right);
} else if (compareResult < 0) {
node.left = remove(t, node.left);
} else if (node.left != null && node.right != null) {
node.element = findMin(node.right).element;
node.right = remove(node.element, node.right);
} else {
node = (node.left != null) ? node.left : node.right;
}
return node;
}
/*
* 打印"二叉查找树"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
private void print(AVLTreeNode<T> tree, T key, int direction) {
if(tree != null) {
if(direction==0) // tree是根节点
System.out.printf("%2d is root\n", tree.element, key);
else // tree是分支节点
System.out.printf("%2d is %2d's %6s child\n", tree.element, key, direction==1?"right" : "left");
print(tree.left, tree.element, -1);
print(tree.right,tree.element, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.element, 0);
}
}


