【DP】动态规划专题

背包问题

2. 01背包问题

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1010;

int n, m;
int f[N];

int main()
{
    scanf("%d%d", &n, &m);
    while(n -- )
    {
        int v, w;
        scanf("%d%d", &v, &w);
        for(int j = m; j >= v; j -- )
            f[j] = max(f[j], f[j - v] + w);
    }
    printf("%d", f[m]);
    return 0;
}

写法二：

#include <iostream>

using namespace std;

const int N = 1010;

int n,m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i ++ )
        for(int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);


    cout << f[m] << endl;

    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1397858/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

3. 完全背包问题

#include <iostream>

using namespace std;

const int N = 1010;

int n,m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i ++ )
        for(int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);


    cout << f[m] << endl;
    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1398967/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

4. 多重背包问题 I

#include <iostream>

using namespace std;

const int N = 110;

int n,m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i];

    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
            for(int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);

    cout << f[n][m] << endl;
    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1401139/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

5. 多重背包问题 II

#include <iostream>

using namespace std;

const int N = 25000;

int n,m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    int cnt = 0;

    for(int i = 1; i <= n; i ++ )
    {
        int a,b,s;
        cin >> a >> b >> s;

        //二进制优化
        int k = 1;
        while(k <= s)
        {
            cnt ++ ;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }

        if(s > 0) //还剩下一最后一组（即差一部分不能用2的整数次幂表示的部分）
        {
            cnt ++ ;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }

    }
    n = cnt;

    for(int i = 1; i <= n; i ++ )
        for(int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);


    cout << f[m] << endl;

    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1401182/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

6. 多重背包问题 III

单调队列优化

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 20010;

int n, m;
int f[N], g[N], q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i ++ )
    {
        int v, w, s;
        scanf("%d%d%d", &v, &w, &s);
        memcpy(g, f, sizeof f);
        for(int j = 0; j < v; j ++ )
        {
            int hh = 0, tt = -1;
            for(int k = j; k <= m; k += v )
            {
                while(hh <= tt && q[hh] < k - s * v) hh ++ ;
                if(hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);
                while(hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt -- ;
                q[ ++ tt ] = k;
            }
        }

    }

    printf("%d\n", f[m]);

    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1542933/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

7. 混合背包问题

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1010;

int n, m;
int f[N];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++ )
    {
        int v, w ,s;
        scanf("%d%d%d", &v, &w, &s);
        if(s == 0) //完全背包问题
        {
            for(int j = v; j <= m; j ++ )
                f[j] = max(f[j], f[j - v] + w);
        }
        else //01背包或者多重背包（01背包是s=1时多重背包的特殊情况，可以合并在一起写）
        {
            if(s == -1) s = 1; //如果是01背包，将s设置为1即可
            for(int k = 1; k <= s; k *= 2 ) //二进制优化
            {
                for(int j = m; j >= k * v; j -- )
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;    
            }
            if(s) //如果s不为0，即还有剩下的部分
            {
                for(int j = m; j >= s * v; j -- )
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    printf("%d\n", f[m]);
    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1559531/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

8. 二维费用的背包问题

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1010;

int n, V, M;
int f[N][N];

int main()
{
    scanf("%d%d%d", &n, &V, &M);
    for(int i = 0; i < n; i ++ )
    {
        int v, m, w;
        scanf("%d%d%d", &v, &m, &w);
        for(int j = V; j >= v; j -- )
            for(int k = M; k >= m; k -- )
                f[j][k] = max(f[j][k], f[j - v][k - m] + w);
    }

    printf("%d\n", f[V][M]);
    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1547333/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

9. 分组背包问题

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int f[N];
int v[N][N], w[N][N], s[N];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i ++ )
    {
        scanf("%d", &s[i]);
        for(int j = 0; j < s[i]; j ++ )
        {
            scanf("%d%d", &v[i][j], &w[i][j]);
        }
    }

    for(int i = 0; i < n; i ++ )
        for(int j = m; j >= 0; j -- )
            for(int k = 0;  k < s[i]; k ++ )
                if(j >= v[i][k]) 
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    printf("%d\n", f[m]);
    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1401214/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

10. 有依赖的背包问题

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 110;

int n, m;
int f[N][N], v[N], w[N];
int h[N], e[N], ne[N], idx;

void add(int a, int b) // 建立一条由a指向b的边
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++ ;
}

void dfs(int u)
{
    for(int i = h[u]; i != -1; i = ne[i]) // i != -1 可以简写为~i
    {
        int son = e[i];
        dfs(son);

        //分组背包
        for(int j = m - v[u]; j >= 0; j -- )
            for(int k = 0; k <= j; k ++ )
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
    }

    //将物品u加进去
    for(int i = m; i >= v[u]; i -- ) f[u][i] = f[u][i -v[u]] + w[u];
    for(int i = 0; i < v[u]; i ++ ) f[u][i] = 0;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);

    int root;
    for(int i = 1; i <= n; i ++ )
    {
        int p;
        scanf("%d%d%d", &v[i], &w[i], &p);
        if(p == -1) root = i;
        else add(p, i); // 建立从父结点p指向当前结点i的边
    }

    dfs(root);

    printf("%d\n", f[root][m]);

    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1560301/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

11. 背包问题求方案数

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n, m;
int f[N], g[N];

int main()
{
    scanf("%d%d", &n, &m);

    memset(f, -0x3f, sizeof f);
    f[0] = 0;
    g[0] = 1;

    for(int i = 1; i <= n; i ++ )
    {
        int v, w;
        scanf("%d%d", &v, &w);
        for(int j = m; j >= v; j -- )
        {
            int maxv = max(f[j], f[j - v] + w);
            int cnt = 0;
            if(maxv == f[j]) cnt += g[j];
            if(maxv == f[j - v] + w) cnt += g[j - v];
            g[j] = cnt % mod;
            f[j] = maxv;
        }
    }

    int res = 0;
    for(int i = 0; i <= m; i ++ ) res = max(res, f[i]);

    int cnt = 0;
    for(int i = 0; i <= m; i ++ )
    {
        if(res == f[i]) cnt = (cnt + g[i]) % mod;
    }

    printf("%d\n", cnt);
    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1561642/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

12. 背包问题求具体方案

求具体方案则不能压缩空间，必须用两维

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int f[N][N];
int v[N], w[N];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++ ) scanf("%d%d", &v[i], &w[i]);

    for(int i = n; i >= 1; i -- )
    {
        for(int j = 0; j <= m; j ++ )
        {
            f[i][j] = f[i + 1][j]; //从大往小更新，所以从f[i + 1]开始
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    }

    int j = m;
    for(int i = 1; i <= n; i ++ )
    {
        if(j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
        {
            printf("%d ", i);
            j -= v[i];
        }
    }

    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1552070/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

写法二：

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++ ) scanf("%d%d", &v[i], &w[i]);
    
    for(int i = n; i; i -- )
    {
        for(int j = 0; j <= m; j ++ )
        {
            f[i][j] = f[i + 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    }
    
    int i = 1, j = m;
    while(i <= n)
    {
        if(j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
        {
            printf("%d ", i);
            j -= v[i];
            i ++ ;
        }
        else i ++ ;
    }
    return 0;
}

数字三角形模型

最长上升子序列模型

895. 最长上升子序列

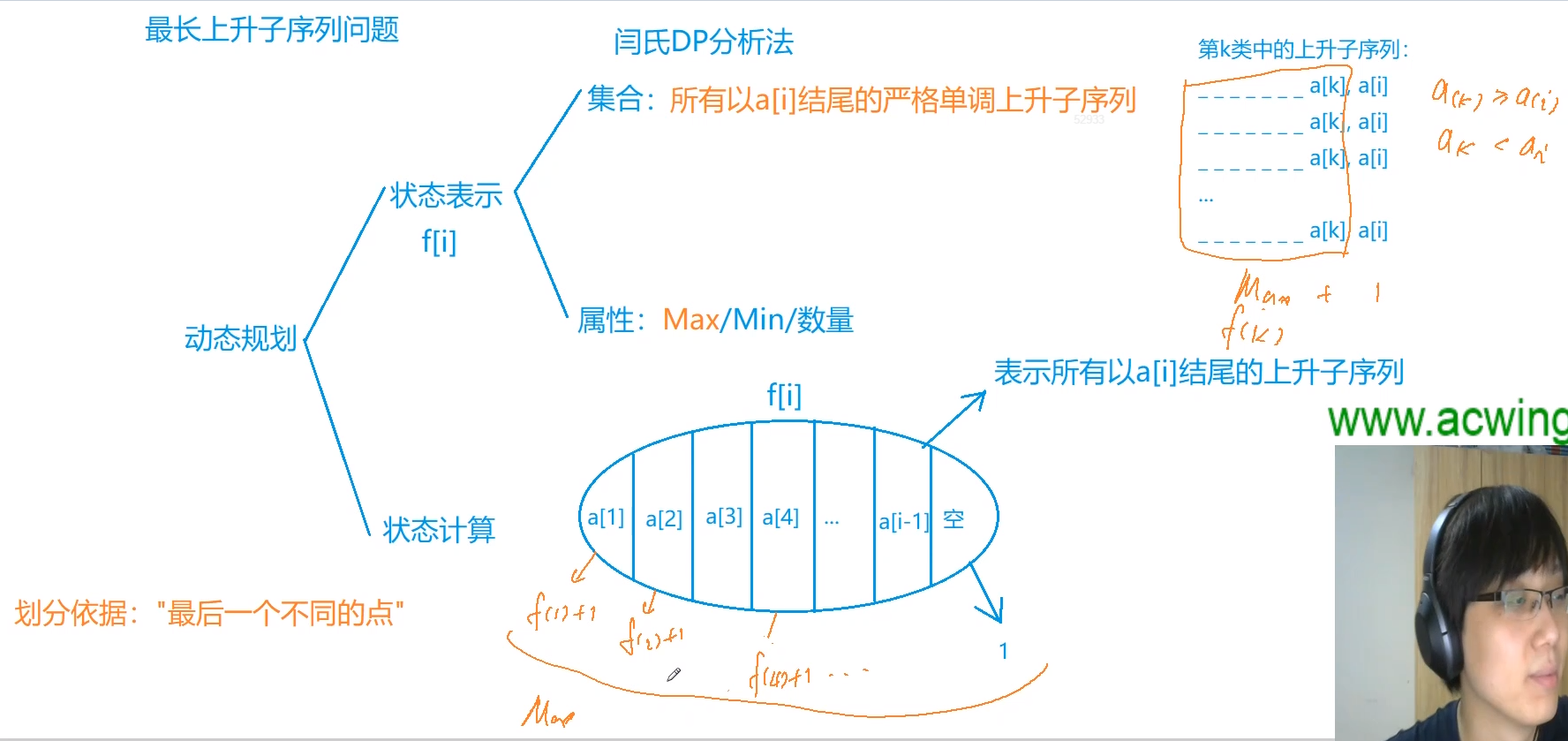
#include <iostream>

using namespace std;

const int N = 1010;

int n;
int a[N], f[N];

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    
    for(int i = 1; i <= n; i ++ )
    {
        f[i] = 1;
        for(int j = 1; j < i; j ++ )
        {
            if(a[j] < a[i])
                f[i] = max(f[i], f[j] + 1);
        }
    }   
    int res = 0;
    for(int i = 1; i <= n; i ++ ) res = max(res, f[i]);
    printf("%d\n", res);
    
    return 0;
}

896. 最长上升子序列 II

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e6 + 10;

int n;
int q[N], a[N];

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    
    int len = 0;
    q[0] = -2e9;
    for(int i = 0; i < n; i ++ )
    {
        int l = 0, r = len;
        while(l < r)
        {
            int mid = l + r + 1 >> 1;
            if(q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }
    printf("%d\n", len);
    return 0;
}

最长公共子序列模型

897. 最长公共子序列

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n,m;
char a[N], b[N];
int f[N][N];

int main()
{
    scanf("%d%d",&n,&m);
    scanf("%s%s",a + 1, b + 1);

    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
        {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
        }

    printf("%d\n", f[n][m]);
    return 0;
}

作者：Once.
链接：https://www.acwing.com/activity/content/code/content/1413988/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

状态压缩DP

状态机模型

区间DP

树形DP

数位统计DP

记忆化搜索