【数据结构】二叉树题单
AcWing PAT甲级树专题
1476. 数叶子结点
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110;
int h[N], e[N], ne[N], idx;
int n, m;
int cnt[N], max_depth;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int depth)
{
if(h[u] == -1) //是叶子结点
{
cnt[depth] ++ ;
max_depth = max(max_depth, depth);
return;
}
for(int i = h[u]; i != -1; i = ne[i])
{
dfs(e[i], depth + 1);
}
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
while(m -- )
{
int id, k;
scanf("%d%d", &id, &k);
while(k -- )
{
int son;
scanf("%d", &son);
add(id, son);
}
}
dfs(1, 0);
printf("%d", cnt[0]);
for(int i = 1; i <= max_depth; i ++ ) printf(" %d", cnt[i]);
puts("");
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1817723/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1497. 树的遍历
#include <iostream>
#include <cstring>
#include <unordered_map>
using namespace std;
const int N = 40;
int n;
unordered_map<int, int> l, r, pos;
int inorder[N], postorder[N];
int q[N];
int build(int il, int ir, int pl, int pr) //il,ir分别为中序遍历的左右子树边界,pl,pr为后序遍历的左右子树边界
{
int root = postorder[pr]; //后序遍历的最后一个结点是根结点
int k = pos[root]; //k是根结点在中序遍历中的下标
if(il < k) //如果左子树存在
{
l[root] = build(il, k - 1, pl, pl + (k - 1 - il));
}
if(k < ir) //如果右子树存在
{
r[root] = build(k + 1, ir, pl + (k - 1 - il) + 1, pr - 1);
}
return root;
}
void bfs(int root)
{
int hh = 0, tt = 0;
q[0] = root;
while(hh <= tt)
{
int t = q[hh ++ ];
if(l.count(t)) q[++ tt] = l[t];
if(r.count(t)) q[++ tt] = r[t];
}
printf("%d", q[0]);
for(int i = 1; i < n; i ++ ) printf(" %d", q[i]);
puts("");
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i ++ ) scanf("%d", &postorder[i]);
for(int i = 0; i < n; i ++ )
{
scanf("%d", &inorder[i]);
pos[inorder[i]] = i;
}
int root = build(0, n - 1, 0, n - 1);
bfs(root);
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1817758/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1498. 最深的根
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int N = 1e4 + 10, M = N * 2;
int n;
int h[N], e[M], ne[M], idx;
int p[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int find(int x)
{
return x == p[x] ? x : p[x] = find(p[x]);
}
int dfs(int u, int father)
{
int depth = 0;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(j == father) continue;
depth = max(depth, dfs(j, u) + 1);
}
return depth;
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d", &n);
for(int i = 1; i <= n; i ++ ) p[i] = i;
int cnt = n; //cnt为连通块的数量,一开始每个点都是一个连通块(n个点)
for(int i = 0; i < n - 1; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
if(find(a) != find(b))
{
p[find(a)] = find(b);
cnt -- ;
}
add(a, b), add(b, a);
}
if(cnt > 1) printf("Error: %d components", cnt);
else
{
vector<int> nodes;
int max_depth = -1;
for(int i = 1; i <= n; i ++ )
{
int depth = dfs(i, -1);
if(depth > max_depth)
{
max_depth = depth;
nodes.clear();
nodes.push_back(i);
}
else if(depth == max_depth)
{
nodes.push_back(i);
}
}
for(auto c : nodes) printf("%d\n", c);
}
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1818061/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1527. 判断二叉搜索树
二叉搜索树的中序遍历结果一定是有序的
所以根据其前序遍历可以求出中序遍历,进而构建出整个二叉搜索树.
无解的情况:在中序遍历中找不到根结点,直接return即可。
镜像之后的中序遍历为降序(镜像前的中序遍历为升序)

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
int n;
int preorder[N], inorder[N];
int postorder[N], cnt;
bool build(int il, int ir, int pl, int pr, int type) //il,ir分别为中序遍历的左右边界,pl,pr分别为前序遍历左右边界
{
if(il > ir) return true;
int root = preorder[pl];
int k;
if(type == 0)
{
for(k = il; k <= ir; k ++ )
if(inorder[k] == root)
break;
if(k > ir) return false; //在中序遍历中没有找到根结点
}
else
{
for(k = ir; k >= il; k -- )
if(inorder[k] == root)
break;
if(k < il) return false; //在中序遍历中没有找到根结点
}
bool res = true;
//因为是后序遍历,所以先遍历左右子树,后遍历根结点,下面这两句话其实起到了遍历左右子树的效果
if(!build(il, k - 1, pl + 1, pl + 1 + (k - 1 - il), type)) res = false;
if(!build(k + 1, ir, pl + 1 + (k - 1 - il) + 1, pr, type)) res = false;
postorder[cnt ++ ] = root;
return res;
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i ++ )
{
scanf("%d", &preorder[i]);
inorder[i] = preorder[i];
}
sort(inorder, inorder + n);
if(build(0, n - 1, 0, n - 1, 0)) //原树
{
puts("YES");
printf("%d", postorder[0]);
for(int i = 1; i < n; i ++ ) printf(" %d", postorder[i]);
puts("");
}
else //镜像树
{
reverse(inorder, inorder + n);
cnt = 0;
if(build(0, n - 1, 0, n - 1, 1))
{
puts("YES");
printf("%d", postorder[0]);
for(int i = 1; i < n; i ++ ) printf(" %d", postorder[i]);
puts("");
}
else puts("NO");
}
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1818225/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1550. 完全二叉搜索树

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int w[N], tr[N];
void dfs(int u, int& k)
{
if(u * 2 <= n) dfs(u * 2, k);
tr[u] = w[k ++ ];
if(u * 2 + 1 <= n) dfs(u * 2 + 1, k);
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++ ) cin >> w[i];
sort(w, w + n);
int k = 0;
dfs(1, k);
printf("%d", tr[1]);
for(int i = 2; i <= n; i ++ ) printf(" %d", tr[i]);
puts("");
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1819160/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1576. 再次树遍历

#include <iostream>
#include <cstring>
#include <stack>
using namespace std;
const int N = 40;
int n;
int l[N], r[N];
void dfs(int u, int root) //传入根结点是为了方便末尾无空格
{
if(!u) return;
// 后序遍历,先遍历左子树再遍历右子树,最后输出根结点
dfs(l[u], root);
dfs(r[u], root);
printf("%d", u);
if(u != root) printf(" ");
}
int main()
{
scanf("%d", &n);
int root, last = 0, type = -1;
stack<int> stk;
for(int i = 0; i < n * 2; i ++ )
{
char op[10];
scanf("%s", op);
if(!strcmp(op, "Push"))
{
int x;
scanf("%d", &x);
if(last == 0) root = x;
else
{
if(type == 0) l[last] = x;
else r[last] = x;
}
stk.push(x);
last = x;
type = 0; //0表示push,1表示pop
}
else
{
last = stk.top();
stk.pop();
type = 1;
}
}
dfs(root, root);
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1819444/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
先排个序,然后按中序遍历的顺序填入数值即可构建二叉搜索树
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 110;
int n;
int a[N], q[N];
int w[N], l[N], r[N];
void dfs(int u, int &k)
{
if(u == -1) return;
dfs(l[u], k);
w[u] = a[k ++ ];
dfs(r[u], k);
}
void bfs()
{
int hh = 0, tt = 0;
q[0] = 0;
while(hh <= tt)
{
int t = q[hh ++ ];
printf("%d ", w[t]);
if(l[t] != -1) q[++ tt] = l[t];
if(r[t] != -1) q[++ tt] = r[t];
}
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i ++ ) scanf("%d%d", &l[i], &r[i]);
for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
sort(a, a + n);
int k = 0;
dfs(0, k);
bfs();
return 0;
}
1592. 反转二叉树
反转就相当于把每个点的左右儿子交换(轴对称)
#include <iostream>
#include <cstring>
using namespace std;
const int N = 15;
int n;
int l[N], r[N];
int q[N];
bool has_father[N];
void dfs_reverse(int u) //反转二叉树(交换每个结点的左右儿子)
{
if(u == -1) return;
dfs_reverse(l[u]);
dfs_reverse(r[u]);
swap(l[u], r[u]);
}
void bfs(int root) //层序遍历
{
int hh = 0, tt = 0;
q[0] = root;
while(hh <= tt)
{
int t = q[hh ++ ];
if(l[t] != -1) q[++ tt] = l[t];
if(r[t] != -1) q[++ tt] = r[t];
}
printf("%d", q[0]);
for(int i = 1; i < n; i ++ ) printf(" %d", q[i]);
puts("");
}
void dfs(int u, int& k)
{
if(u == -1) return;
//中序遍历
dfs(l[u], k);
printf("%d", u);
if(++ k != n) printf(" ");
dfs(r[u], k);
}
int main()
{
scanf("%d", &n);
memset(l, -1, sizeof l);
memset(r, -1, sizeof r);
for(int i = 0; i < n; i ++ )
{
char lc, rc;
cin >> lc >> rc;
if(lc != '-') l[i] = lc - '0', has_father[l[i]] = true;
if(rc != '-') r[i] = rc - '0', has_father[r[i]] = true;
}
int root = 0;
while(has_father[root]) root ++ ;
dfs_reverse(root);
bfs(root);
int k = 0;
dfs(root, k);
return 0;
}
1600. 完全二叉树
判断完全二叉树的方法:
1.完全二叉树是用数组来存储的,且结点x满足其左儿子为2x,右儿子为2x+1,其父结点为x / 2下取整
2.结点数为n的完全二叉树一定可以存到数组中,且一定正好占满n个位置。
3.对于题目给定的二叉树,我们直接按照完全二叉树的存储规则将其存到数组中,如果其不是完全二叉树,那么其最后结点在数组中的下标一定大于n(完全二叉树的数组下标最大为n,n为二叉树中的结点数),即可能出现了某个结点没有左儿子却有右儿子的情况,此时我们就认为其不是一棵完全二叉树。
具体实现时,我们只需按照上述规则求一下每个结点在完全二叉树一维数组中的编号,然后求出所有编号中的最大值,与n作比较,如果最大值大于n,则不是完全二叉树。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 25;
int n;
int l[N], r[N];
bool has_father[N];
int maxk, maxid;
void dfs(int u, int k) //u为当前传入的结点,k为结点编号
{
if(u == -1) return;
if(k > maxk)
{
maxk = k;
maxid = u;
}
dfs(l[u], k * 2);
dfs(r[u], k * 2 + 1);
}
int main()
{
memset(l, -1, sizeof l);
memset(r, -1, sizeof r);
scanf("%d", &n);
for(int i = 0; i < n; i ++ )
{
string a, b;
cin >> a >> b;
if(a != "-") l[i] = stoi(a), has_father[l[i]] = true;
if(b != "-") r[i] = stoi(b), has_father[r[i]] = true;
}
int root = 0;
while(has_father[root]) root ++ ;
dfs(root, 1); //根结点编号为1
if(maxk == n) printf("YES %d\n", maxid);
else printf("NO %d\n", root);
return 0;
}
1605. 二叉搜索树最后两层结点数量
#include <iostream>
using namespace std;
const int N = 1010;
int n;
int l[N], r[N], v[N], idx;
int cnt[N], max_depth;
void insert(int& u, int w)
{
if(!u)
{
u = ++ idx ;
v[u] = w;
}
else if(w <= v[u]) insert(l[u], w);
else insert(r[u], w);
}
void dfs(int u, int depth)
{
if(u == 0) return;
cnt[depth] ++ ;
max_depth = max(max_depth, depth);
dfs(l[u], depth + 1);
dfs(r[u], depth + 1);
}
int main()
{
scanf("%d", &n);
int root = 0;
for(int i = 0; i < n; i ++ )
{
int w;
scanf("%d", &w);
insert(root, w);
}
dfs(root, 0);
int n1 = cnt[max_depth], n2 = cnt[max_depth - 1];
printf("%d + %d = %d\n", n1, n2, n1 + n2);
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1820854/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1609. 前序和后序遍历
#include <iostream>
using namespace std;
const int N = 40;
int n;
int pre[N], post[N];
int dfs(int l1, int r1, int l2, int r2, string& in)
{
if(l1 > r1) return 1;
if(pre[l1] != post[r2]) return 0;
int cnt = 0;
for(int i = l1; i <= r1; i ++ )
{
string lin, rin;
int lcnt = dfs(l1 + 1, i, l2, l2 + i - l1 - 1, lin);
int rcnt = dfs(i + 1, r1, l2 + i - l1 - 1 + 1, r2 - 1, rin);
if(lcnt && rcnt)
{
in = lin + to_string(pre[l1]) + ' ' + rin;
cnt += lcnt * rcnt;
if(cnt > 1) break;
}
}
return cnt;
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++ ) cin >> pre[i];
for(int i = 0; i < n; i ++ ) cin >> post[i];
string in;
int cnt = dfs(0, n - 1, 0, n - 1, in);
if(cnt > 1) puts("No");
else puts("Yes");
in.pop_back();
cout << in << endl;
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1820959/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1620. Z 字形遍历二叉树
实现z字形遍历的方法:
实际上还是层序遍历,把奇数层的遍历结果reverse一下即可。
剩下的就是构建二叉树了,由中序遍历和后序遍历递归构建二叉树:
1.先在后序遍历中找到根结点,然后在中序遍历中找到根结点的位置
2.中序遍历中根结点的左边是左子树,根结点右边是右子树,由此得出区间长度(左子树的结点数和右子树结点数)。
3.写一个build函数,传入左子树的中序遍历和后序遍历的区间左右端点,递归构建左子树
再传入右子树的中序遍历和后序遍历的区间左右端点,递归构建右子树。
建立好树以后再用BFS做一遍层序遍历即可。
建树时每个点只会遍历一次,时间复杂度,BFS每个点遍历一次,也是,所以整体时间复杂度为

#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 40;
int n;
unordered_map<int, int> l, r, pos;
int in[N], post[N];
int q[N];
int build(int il, int ir, int pl, int pr)
{
int root = post[pr];
int k = pos[root];
if(il < k) l[root] = build(il, k - 1, pl, pl + (k - 1 - il));
if(k < ir) r[root] = build(k + 1, ir, pl + (k - 1 - il) + 1, pr - 1);
return root;
}
void bfs(int root)
{
int hh = 0, tt = 0;
q[0] = root;
int step = 0;
while(hh <= tt)
{
int head = hh, tail = tt;
while(hh <= tail)
{
int t = q[hh ++ ];
if(l.count(t)) q[++ tt] = l[t];
if(r.count(t)) q[++ tt] = r[t];
}
if(++ step % 2) reverse(q + head, q + tail + 1);
}
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++ )
{
cin >> in[i];
pos[in[i]] = i;
}
for(int i = 0; i < n; i ++ ) cin >> post[i];
int root = build(0, n - 1, 0, n - 1);
bfs(root);
cout << q[0];
for(int i = 1; i < n; i ++ ) cout << ' ' << q[i];
cout << endl;
return 0;
}
1631. 后序遍历
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 5e4 + 10;
int n;
int pre[N], inorder[N];
unordered_map<int, int> pos;
int post[N], cnt;
void build(int il, int ir, int pl, int pr)
{
int root = pre[pl]; //前序遍历的第一个点是根结点
int k = pos[root]; //在中序遍历中找到根结点的下标
if(il < k) build(il, k - 1, pl + 1, pl + 1 + k - 1 - il); //如果左子树存在,递归建立左子树
if(k < ir) build(k + 1, ir, pl + 1 + k - 1 - il + 1, pr); //如果右子树存在,递归建立右子树
post[cnt ++ ] = root; //也可以求出整个后序遍历,输出post[0]即可
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++ ) cin >> pre[i];
for(int i = 0; i < n; i ++ )
{
cin >> inorder[i];
pos[inorder[i]] = i;
}
build(0, n - 1, 0, n - 1);
cout << post[0] << endl;
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1821437/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1552. AVL树的根
一个性质:左旋和右旋不会改变树的中序遍历。

右旋的步骤:
原来根A的左儿子B变成新的根,先把B存下来int p = l[u]
原来根A的左儿子变成B的右儿子,l[u] = r[p] , l[u]表示u的左儿子,r[p]表示p的右儿子
B的右儿子就变成了原来的根A, r[p] = u
int p = l[u]; //原来根A的左儿子B先存在来,它将是新的根
l[u] = r[p]; //原来根A的左儿子变成其左儿子B的右儿子E
r[p] = u; //原来根A的左儿子B变成新的根(儿子篡位了hh)
左旋的步骤:
int p = r[u]; //原来根B的右儿子A先存下来,它将是新的根
r[u] = l[p]; //原来根B的右儿子变成其右儿子A的左儿子E
l[p] = u; //原来根B的右儿子A变成新的根

#include <iostream>
using namespace std;
const int N = 30;
int l[N], r[N], v[N], idx;
int h[N]; //高度
void update(int u) //更新树的高度
{
h[u] = max(h[l[u]], h[r[u]]) + 1;
}
void R(int& u)
{
int p = l[u];
l[u] = r[p], r[p] = u;
update(u), update(p);
u = p;
}
void L(int& u)
{
int p = r[u];
r[u] = l[p], l[p] = u;
update(u), update(p);
u = p;
}
int get_balance(int u) //求一下左子树的高度-右子树的高度
{
return h[l[u]] - h[r[u]];
}
void insert(int& u, int w)
{
if(u == 0) u = ++ idx, v[u] = w;
else if(w < v[u])
{
insert(l[u], w);
if(get_balance(u) == 2)
{
if(get_balance(l[u]) == 1) R(u);
else L(l[u]), R(u);
}
}
else
{
insert(r[u], w);
if(get_balance(u) == -2)
{
if(get_balance(r[u]) == -1) L(u);
else R(r[u]), L(u);
}
}
update(u);
}
int main()
{
int n, root = 0;
cin >> n;
while(n -- )
{
int w;
cin >> w;
insert(root, w);
}
cout << v[root] << endl;
return 0;
}
1616. 判断完全 AVL 树
#include <iostream>
using namespace std;
const int N = 30;
int n;
int l[N], r[N], v[N], h[N], idx;
int q[N], pos[N];
void update(int u)
{
h[u] = max(h[l[u]], h[r[u]]) + 1;
}
void R(int& u)
{
int p = l[u];
l[u] = r[p], r[p] = u;
update(u), update(p);
u = p;
}
void L(int& u)
{
int p = r[u];
r[u] = l[p], l[p] = u;
update(u), update(p);
u = p;
}
int get_balance(int u)
{
return h[l[u]] - h[r[u]];
}
void insert(int& u, int w)
{
if(u == 0) u = ++ idx, v[u] = w;
else if(w < v[u])
{
insert(l[u], w);
if(get_balance(u) == 2)
{
if(get_balance(l[u]) == 1) R(u);
else L(l[u]), R(u);
}
}
else
{
insert(r[u], w);
if(get_balance(u) == -2)
{
if(get_balance(r[u]) == -1) L(u);
else R(r[u]), L(u);
}
}
update(u);
}
bool bfs(int root)
{
int hh = 0, tt = 0;
q[0] = root;
pos[root] = 1;
bool res = true;
while(hh <= tt)
{
int t = q[hh ++ ];
if(pos[t] > n) res = false;
if(l[t]) q[++ tt ] = l[t], pos[l[t]] = pos[t] * 2; //左儿子下标是父结点下标的2倍
if(r[t]) q[++ tt ] = r[t], pos[r[t]] = pos[t] * 2 + 1; //右儿子下标是父结点下标的2倍+1
}
return res;
}
int main()
{
int root = 0;
cin >> n;
for(int i = 0; i < n; i ++ )
{
int w;
cin >> w;
insert(root, w);
}
bool res = bfs(root);
cout << v[q[0]];
for(int i = 1; i < n; i ++ ) cout << ' ' << v[q[i]];
cout << endl;
if(res) puts("YES");
else puts("NO");
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1821953/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1628. 判断红黑树
1.红黑树是二叉搜索树,所以将前序遍历的序列排序即可得到中序遍历的序列
2.然后由前序序列和中序序列构建出整个二叉搜索树
3.分别判断:(1)根是黑色(2)红色点的左右儿子是黑色(3)从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 40;
int pre[N], in[N];
unordered_map<int, int> pos;
bool ans;
int build(int il, int ir, int pl, int pr, int& sum)
{
int root = pre[pl];
int k = pos[abs(root)];
if(k < il || k > ir)
{
ans = false;
return 0;
}
int left = 0, right = 0, ls = 0, rs = 0;
if(il < k) left = build(il, k - 1, pl + 1, pl + 1 + k - 1 - il, ls);
if(k < ir) right = build(k + 1, ir, pl + 1 + k - 1 - il + 1, pr, rs);
if(ls != rs) ans = false;
sum = ls;
if(root < 0)
{
if(left < 0 || right < 0) ans = false;
}
else sum ++ ;
return root;
}
int main()
{
int T;
cin >> T;
while(T -- )
{
int n;
cin >> n;
for(int i = 0; i < n; i ++ )
{
cin >> pre[i];
in[i] = abs(pre[i]);
}
sort(in, in + n);
pos.clear();
for(int i = 0; i < n; i ++ ) pos[in[i]] = i;
ans = true;
int sum = 0;
int root = build(0, n - 1, 0, n - 1, sum);
if(root < 0) ans = false;
if(!ans) puts("No");
else puts("Yes");
}
return 0;
}
1539. 等重路径
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 110;
int n, m, S;
int w[N];
bool g[N][N];
vector<vector<int>> ans;
void dfs(int u, int s, vector<int>& path)
{
bool is_leaf = true;
for(int i = 0; i < n; i ++ )
{
if(g[u][i])
{
is_leaf = false;
break;
}
}
if(is_leaf)
{
if(s == S) ans.push_back(path);
}
else
{
for(int i = 0; i < n; i ++ )
{
if(g[u][i])
{
path.push_back(w[i]);
dfs(i, s + w[i], path);
path.pop_back();
}
}
}
}
int main()
{
cin >> n >> m >> S;
for(int i = 0; i < n; i ++ ) cin >> w[i];
while(m -- )
{
int id, k;
cin >> id >> k;
while(k -- )
{
int son;
cin >> son;
g[id][son] = true;
}
}
vector<int> path({w[0]});
dfs(0, w[0], path);
sort(ans.begin(), ans.end(), greater<vector<int>>());
for(auto p : ans)
{
cout << p[0];
for(int i = 1; i < p.size(); i ++ ) cout << ' ' << p[i];
cout << endl;
}
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1823634/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1584. 最大的一代
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 110;
int n, m;
bool g[N][N];
vector<int> level[N];
int main()
{
cin >> n >> m;
while(m -- )
{
int id, k;
cin >> id >> k;
while(k -- )
{
int son;
cin >> son;
g[id][son] = true;
}
}
level[1].push_back(1);
int l = 1;
while(level[l].size())
{
for(auto ver : level[l])
{
for(int j = 1; j <= n; j ++ )
{
if(g[ver][j])
{
level[l + 1].push_back(j);
}
}
}
l ++ ;
}
int k = 1;
for(int i = 1; i < l; i ++ )
{
if(level[i].size() > level[k].size())
{
k = i;
}
}
cout << level[k].size() << ' ' << k << endl;
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1824218/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1649. 堆路径
#include <iostream>
#include <vector>
using namespace std;
const int N = 1010;
int n;
int h[N];
bool gt, lt;
vector<int> path;
void dfs(int u)
{
path.push_back(h[u]);
if(u * 2 > n) //叶结点
{
cout << path[0];
for(int i = 1; i < path.size(); i ++ )
{
cout << ' ' << path[i];
if(path[i] > path[i - 1]) gt = true;
else if(path[i] < path[i - 1]) lt = true;
}
cout << endl;
}
//因为题目要求先输出右子树后输出左子树,所以先遍历右子树
if(u * 2 + 1 <= n) dfs(u * 2 + 1);
if(u * 2 <= n) dfs(u * 2);
path.pop_back();
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ ) cin >> h[i];
dfs(1);
if(gt && lt) puts("Not Heap");
else if(lt) puts("Max Heap"); //lt:只存在后一个比前一个小的情况
else puts("Min Heap");
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1825044/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1623. 中缀表达式
#include <iostream>
using namespace std;
const int N = 25;
int n;
int l[N], r[N];
string w[N];
bool has_father[N], is_leaf[N];
string dfs(int u)
{
string left, right;
if(l[u] != -1)
{
left = dfs(l[u]);
if(!is_leaf[l[u]]) left = "(" + left + ")"; //不是叶结点则要加括号
}
if(r[u] != -1)
{
right = dfs(r[u]);
if(!is_leaf[r[u]]) right = "(" + right + ")";
}
return left + w[u] + right;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ )
{
cin >> w[i] >> l[i] >> r[i];
if(l[i]) has_father[l[i]] = true;
if(r[i]) has_father[r[i]] = true;
if(l[i] == -1 && r[i] == -1) is_leaf[i] = true;
}
//找到根结点
int root = 1;
while(has_father[root]) root ++ ; //根结点是没有父结点的点
cout << dfs(root) << endl;
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1825144/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1636. 最低公共祖先
有关树的基本操作:已知中序遍历序列和前序(后序)序列,构造出整个二叉树。
对于二叉搜索树(BST),已知前序遍历序列,则可以推出中序遍历序列
因为二叉搜索树的中序遍历是有序的,所以只需要把前序遍历序列排个序,所得序列即为中序遍历序列。
然后由前序和中序遍历序列构建整个二叉搜索树。
求最近公共祖先的方法:
先标记每个点的深度,对于询问的两个点,先把较深的那个点上移至与另一个点相同的深度
然后将两个点同时上移,当移到同一个点上时,这个点就是这两个点的最近公共祖先。
然后本题数据较大,需要做一下离散化,方便用数组来代替哈希表,优化常数(否则会超时)。
#include <iostream>
#include <algorithm>
#include <cstring>
#include <unordered_map>
using namespace std;
const int N = 1e4 + 10;
int m, n;
int in[N], pre[N], seq[N]; //seq是原序列,in和pre存的都是离散化之后(0~n-1)的值
unordered_map<int, int> pos;
int p[N], depth[N];
int build(int il, int ir, int pl, int pr, int d) //d为深度
{
int root = pre[pl];
int k = root;
depth[root] = d;
if(il < k) p[build(il, k - 1, pl + 1, pl + 1 + (k - 1 - il), d + 1)] = root;
if(k < ir) p[build(k + 1, ir, pl + 1 + (k - 1 - il) + 1, pr, d + 1)] = root;
return root;
}
int main()
{
scanf("%d%d", &m, &n);
for(int i = 0; i < n; i ++ )
{
scanf("%d", &pre[i]);
seq[i] = pre[i];
}
sort(seq, seq + n);
for(int i = 0; i < n; i ++ )
{
pos[seq[i]] = i;
in[i] = i;
}
for(int i = 0; i < n; i ++ )
{
pre[i] = pos[pre[i]];
}
build(0, n - 1, 0, n - 1, 0); //最后一个参数是深度
while(m -- )
{
int a, b;
scanf("%d%d", &a, &b);
if(pos.count(a) && pos.count(b))
{
a = pos[a], b = pos[b];
int x = a, y = b;
//如果a,b存在的话,则一定存在公共祖先(因为根是所有点的最近公共祖先)
while(a != b)
{
if(depth[a] < depth[b]) b = p[b];
else a = p[a];
}
//while循环结束时a存的就是最近公共祖先
if(a != x && a != y) printf("LCA of %d and %d is %d.\n", seq[x], seq[y], seq[a]);
else if(a == x) printf("%d is an ancestor of %d.\n", seq[x], seq[y]);
else printf("%d is an ancestor of %d.\n", seq[y], seq[x]);
}
else if(pos.count(a) == 0 && pos.count(b) == 0)
{
printf("ERROR: %d and %d are not found.\n", a, b);
}
else if(pos.count(a) == 0)
{
printf("ERROR: %d is not found.\n", a);
}
else
{
printf("ERROR: %d is not found.\n", b);
}
}
return 0;
}
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/1825233/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1644. 二叉树中的最低公共祖先
关于离散化:将中序遍历的每个值映射到0~n-1,然后将前序遍历中也做相同映射,让两个序列中相同的值所对应的下标相同
比如在中序遍历中8映射到0~n-1的下标为7,则其在前序遍历中的下标也应该为7。
也就是说,中序遍历序列中的值映射到0~n-1(有序排序),前序遍历序列中的下标也是按照0~n-1来映射,只是0~n-1不是有序排列。
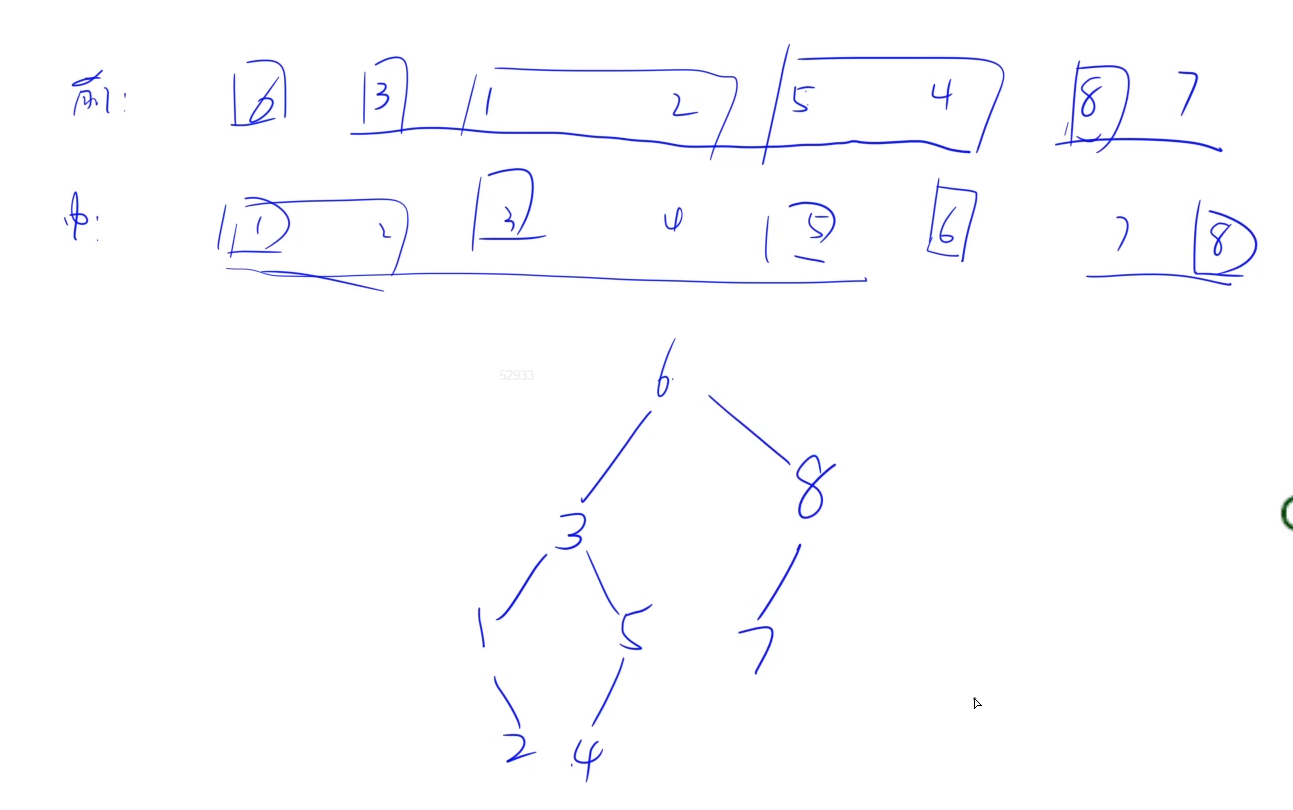
拿样例举例:

#include <iostream>
#include <algorithm>
#include <cstring>
#include <unordered_map>
using namespace std;
const int N = 1e4 + 10;
int m, n;
int pre[N], in[N], seq[N];
unordered_map<int, int> pos;
int p[N], depth[N];
int build(int il, int ir, int pl, int pr, int d)
{
int root = pre[pl];
int k = root;
depth[root] = d;
if(il < k) p[build(il, k - 1, pl + 1, pl + 1 + (k - 1 - il), d + 1)] = root;
if(k < ir) p[build(k + 1, ir, pl + 1 + (k - 1 - il) + 1, pr, d + 1)] = root;
return root;
}
int main()
{
scanf("%d%d", &m, &n);
for(int i = 0; i < n; i ++ )
{
scanf("%d", &seq[i]);
pos[seq[i]] = i;
in[i] = i;
}
for(int i = 0; i < n; i ++ )
{
//scanf("%d", pre[i]); //这里不知道为什么不能用scanf读。。一直报Segmentation Fault
cin >> pre[i];
pre[i] = pos[pre[i]];
}
build(0, n - 1, 0, n - 1, 0);
while(m -- )
{
int a, b;
cin >> a >> b;
if(pos.count(a) && pos.count(b)) //看一下a,b所对应的下标是否存在
{
a = pos[a], b = pos[b]; //将a,b变成离散化后的下标, seq[]就是再变回原来的值
int x = a, y = b;
while(a != b)
{
if(depth[a] > depth[b]) a = p[a];
else b = p[b];
}
if(a != x && a != y) printf("LCA of %d and %d is %d.\n", seq[x], seq[y], seq[a]);
else if(a == x) printf("%d is an ancestor of %d.\n", seq[x], seq[y]);
else printf("%d is an ancestor of %d.\n", seq[y], seq[x]);
}
else if(pos.count(a) == 0 && pos.count(b) == 0)
printf("ERROR: %d and %d are not found.\n", a, b);
else if(pos.count(a) == 0)
printf("ERROR: %d is not found.\n", a);
else
printf("ERROR: %d is not found.\n", b);
}
return 0;
}
LeetCode 二叉树专题
94. 二叉树的中序遍历
递归写法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> res;
void dfs(TreeNode* root)
{
if(!root) return;
dfs(root->left);
res.push_back(root->val);
dfs(root->right);
}
vector<int> inorderTraversal(TreeNode* root) {
dfs(root);
return res;
}
};
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/3201627/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
非递归写法(利用栈,固定套路,要求背会)
中序遍历的非递归写法:
1.遍历一棵子树时,将这棵子树的左链全部加入到栈中(因为遍历顺序是左根右)
2.每次取出栈顶元素,遍历栈顶元素,然后删掉栈顶元素(出栈),删完之后看一下这个点是否有右子树,如果有右子树的话就把右子树的左链放到栈里。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res; // 定义答案数组
stack<TreeNode*> stk; // 定义栈
while(root || stk.size()) // 当当前结点非空或栈非空时
{
while(root) // 当当前结点不空时
{
stk.push(root); // 将当前结点入栈
root = root->left; // 当前结点走到其左儿子的位置
}
root = stk.top(); // 将栈顶元素的值取出
stk.pop(); // 将栈顶元素弹出
res.push_back(root->val); // 遍历当前点
root = root->right; // 遍历完之后走到当前结点的右儿子
}
return res; // 返回答案数组
}
};
作者:Once.
链接:https://www.acwing.com/activity/content/code/content/3201627/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
95. 不同的二叉搜索树 II
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<TreeNode*> dfs(int l, int r)
{
if(l > r) return {NULL};
vector<TreeNode*> res;
for(int i = l; i <= r; i ++ )
{
auto left = dfs(l, i - 1), right = dfs(i + 1, r);
for(auto l : left)
{
for(auto r : right)
{
auto root = new TreeNode(i);
root->left = l;
root->right = r;
res.push_back(root);
}
}
}
return res;
}
vector<TreeNode*> generateTrees(int n) {
if(!n) return {};
return dfs(1, n);
}
};
96. 不同的二叉搜索树
class Solution {
public:
int numTrees(int n) {
vector<int> f(n + 1);
f[0] = 1;
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= i; j ++ )
f[i] += f[j - 1] * f[i - j];
return f[n];
}
};
98. 验证二叉搜索树
法一: BST中序遍历严格有序,只需判断当前节点是否比前一个节点大,如果是,继续递归遍历,否则返回false
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
long long pre = LLONG_MIN;
bool dfs(TreeNode* root)
{
if (!root) return true;
if (!dfs(root->left)) return false;
if (root->val <= pre) return false;
pre = root->val;
return dfs(root->right);
}
bool isValidBST(TreeNode* root) {
return dfs(root);
}
};
法二:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> dfs(TreeNode* root)
{
vector<int> res({1, root->val, root->val});
if(root->left)
{
auto t = dfs(root->left);
if(!t[0] || t[2] >= root->val) res[0] = 0;
res[2] = max(res[2], t[2]);
res[1] = min(res[1], t[1]);
}
if(root->right)
{
auto t = dfs(root->right);
if(!t[0] || t[1] <= root->val) res[0] = 0;
res[2] = max(res[2], t[2]);
res[1] = min(res[1], t[1]);
}
return res;
}
bool isValidBST(TreeNode* root) {
if(!root) return true;
return dfs(root)[0];
}
};
99. 恢复二叉搜索树

如何找到被交换的节点?
找逆序对,只有两种情况
1.只有一个逆序对,那么这两个数挨着,交换逆序对的这两个数即可
2.有两个逆序对,隔着比较远,那么第一个逆序对的第一个数和第二个逆序对的第二个数为被交换的数
Morris遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void recoverTree(TreeNode* root) {
TreeNode *first = NULL, *second = NULL, *last = NULL;
// morris 遍历
while (root)
{
if (!root->left) // 如果左子树为空
{
// 遍历当前点,然后遍历右子树
if (last && last->val > root->val) // 出现逆序对
{
if (!first) first = last, second = root; // 第一个逆序对
else second = root; // 第二个逆序对
}
last = root;
root = root->right;
}
else // 存在左子树
{
// 找前驱节点p
auto p = root->left;
while (p->right && p->right != root) p = p->right;
if (!p->right) // 前驱节点指针指向空,第一次遍历
{
// 利用右子树的叶子结点空余的空针存根结点,达到栈的效果,同时节省空间
p->right = root; // 存下根结点,相当于二叉树非递归遍历中栈的作用
root = root->left; // 进入到左子树准备遍历左子树
}
else // 否则的话说明前驱结点右指针不空,说明已经遍历过了,这是第二次遍历
{
p->right = NULL; // 清空前驱结点右指针,遍历当前结点
// 遍历操作,同上边左子树为空的情况
if (last && last->val > root->val)
{
if (!first) first = last, second = root;
else second = root;
}
last = root;
root = root->right;
}
}
}
swap(first->val, second->val);
}
};
100. 相同的树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
return dfs(p, q);
}
bool dfs(TreeNode* p, TreeNode* q)
{
if (!p && !q) return true;
if (!p || !q || p->val != q->val) return false;
return dfs(p->left, q->left) && dfs(p->right, q->right);
}
};
101. 对称二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool dfs(TreeNode* p, TreeNode *q)
{
if(!p && !q) return true;
if(!p || !q || p->val != q->val) return false;
return dfs(p->left, q->right) && dfs(p->right, q->left);
}
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return dfs(root->left, root->right);
}
};
102. 二叉树的层序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
queue<TreeNode*> q;
if(root) q.push(root);
while(q.size())
{
vector<int> level; // 存每层的节点
int len = q.size(); // len为当前层节点数
while(len -- )
{
auto t = q.front();
q.pop();
level.push_back(t->val);
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
res.push_back(level);
}
return res;
}
};
103. 二叉树的锯齿形层序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> res;
queue<TreeNode*> q;
if (root) q.push(root);
int cnt = 0;
while (q.size())
{
vector<int> level;
int len = q.size();
while (len -- )
{
auto t = q.front();
q.pop();
level.push_back(t->val);
if (t->left) q.push(t->left);
if (t->right) q.push(t->right);
}
if (cnt % 2) reverse(level.begin(), level.end());
cnt ++ ;
res.push_back(level);
}
return res;
}
};
104. 二叉树的最大深度
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(!root) return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};
105. 从前序与中序遍历序列构造二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> pos;
TreeNode* build(vector<int>& preorder, vector<int>& inorder, int pl, int pr, int il, int ir)
{
if(pl > pr) return NULL;
auto root = new TreeNode(preorder[pl]);
int k = pos[root->val];
root->left = build(preorder, inorder, pl + 1, pl + 1 + k - 1 - il, il, k - 1);
root->right = build(preorder, inorder, pl + 1 + k - 1 - il + 1, pr, k + 1, ir);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
for(int i = 0; i < inorder.size(); i ++ ) pos[inorder[i]] = i;
return build(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
}
};
106. 从中序与后序遍历序列构造二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> pos;
TreeNode* build(vector<int>& inorder, vector<int>& postorder, int il, int ir, int pl, int pr)
{
if(pl > pr) return NULL;
auto root = new TreeNode(postorder[pr]);
int k = pos[root->val];
root->left = build(inorder, postorder, il, k - 1, pl, pl + k - 1 - il);
root->right = build(inorder, postorder, k + 1, ir, pl + k - 1 - il + 1, pr - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
for(int i = 0; i < inorder.size(); i ++ ) pos[inorder[i]] = i;
return build(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);
}
};
107. 二叉树的层序遍历 II
按照二叉树正常一层一层地遍历完,最后总的结果翻转一下即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> res;
queue<TreeNode*> q;
if(root) q.push(root);
while(q.size())
{
vector<int> level;
int len = q.size();
while(len -- )
{
auto t = q.front();
q.pop();
level.push_back(t->val);
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
res.push_back(level);
}
reverse(res.begin(), res.end());
return res;
}
};
108. 将有序数组转换为二叉搜索树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return build(nums, 0, nums.size() - 1);
}
TreeNode* build(vector<int>& nums, int l, int r)
{
if (l > r) return nullptr;
int mid = l + r >> 1;
auto root = new TreeNode(nums[mid]);
root->left = build(nums, l, mid - 1);
root->right = build(nums, mid + 1, r);
return root;
}
};
109. 有序链表转换二叉搜索树
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
vector<int> a;
for (auto p = head; p; p = p->next) a.push_back(p->val);
return build(a, 0, a.size() - 1);
}
TreeNode* build(vector<int>& a, int l, int r)
{
if (l > r) return nullptr;
int mid = l + r >> 1;
auto root = new TreeNode(a[mid]);
root->left = build(a, l, mid - 1);
root->right = build(a, mid + 1, r);
return root;
}
};
110. 平衡二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool res;
bool isBalanced(TreeNode* root) {
res = true;
dfs(root);
return res;
}
int dfs(TreeNode* root)
{
if (!root) return 0;
int lh = dfs(root->left), rh = dfs(root->right);
if (abs(lh - rh) > 1) res = false;
return max(lh, rh) + 1;
}
};
111. 二叉树的最小深度
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
return dfs(root);
}
int dfs(TreeNode* root)
{
if (!root) return 0;
if (!root->left && !root->right) return 1;
if (root->left && root->right) return min(dfs(root->left), dfs(root->right)) + 1; //左右子树不空
if (root->left) return dfs(root->left) + 1; // 左子树不空
return dfs(root->right) + 1; // 右子树不空
}
};
112. 路径总和
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (!root) return false;
targetSum -= root->val;
if (!root->left && !root->right) return targetSum == 0;
return root->left && hasPathSum(root->left, targetSum) || root->right && hasPathSum(root->right, targetSum);
}
};
113. 路径总和 II
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
dfs(root, targetSum);
return res;
}
void dfs(TreeNode* root, int targetSum)
{
if (!root) return;
path.push_back(root->val);
targetSum -= root->val;
if (!root->left && !root->right)
{
if (targetSum == 0)
res.push_back(path);
}
else
{
if (root->left) dfs(root->left, targetSum);
if (root->right) dfs(root->right, targetSum);
}
path.pop_back();
}
};
116. 填充每个节点的下一个右侧节点指针
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if (!root) return root;
auto source = root;
while (root->left)
{
for (auto p = root; p; p = p->next)
{
p->left->next = p->right;
if (p->next) p->right->next = p->next->left;
}
root = root->left;
}
return source;
}
};
124. 二叉树中的最大路径和
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res;
int dfs(TreeNode* root)
{
if(!root) return 0;
int left = max(0, dfs(root->left)), right = max(0, dfs(root->right));
res = max(res, root->val + left + right);
return root->val + max(left, right);
}
int maxPathSum(TreeNode* root) {
res = -1e9;
dfs(root);
return res;
}
};
129. 求根节点到叶节点数字之和
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int sum;
vector<int> path;
int sumNumbers(TreeNode* root) {
if (!root) return 0;
sum = 0;
dfs(root);
return sum;
}
void dfs(TreeNode* root)
{
path.push_back(root->val);
if (!root->left && !root->right)
{
string line;
for (int i = 0; i < path.size(); i ++ )
line += to_string(path[i]);
sum += stoi(line);
}
else
{
if (root->left) dfs(root->left);
if (root->right) dfs(root->right);
}
path.pop_back();
}
};
144. 二叉树的前序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while(root || stk.size())
{
if(root)
{
res.push_back(root->val);
stk.push(root);
root = root->left;
}
else
{
root = stk.top()->right;
stk.pop();
}
}
return res;
}
};
145. 二叉树的后序遍历
递归写法:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> res;
void dfs(TreeNode* root)
{
if(!root) return;
if(root->left) dfs(root->left);
if(root->right) dfs(root->right);
res.push_back(root->val);
}
vector<int> postorderTraversal(TreeNode* root) {
dfs(root);
return res;
}
};
迭代写法一(acwing):
巧解:我们在前面已经学过了前序遍历的迭代写法。而前序遍历的遍历顺序是“根左右”,我们可以对前序遍历进行修改,使其按照“根右左”的顺序遍历,然后把得到的结果翻转一下得到的“左右根”序列就是后序遍历的结果。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while(root || stk.size())
{
while(root)
{
res.push_back(root->val);
stk.push(root);
root = root->right; //这里是从前序遍历的root=root->left修改为right
}
root = stk.top()->left; // 从前序遍历的right修改为left
stk.pop();
}
reverse(res.begin(), res.end()); //翻转得到的“根右左”序列得到“左右根”序列
return res;
}
};
迭代写法二(巧解):参考题解

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
if(!root) return res;
stack<TreeNode*> stk;
stk.push(root);
while(stk.size())
{
auto t = stk.top();
stk.pop();
if(t) // 如果当前节点不空
{
stk.push(t);
stk.push(NULL);
//先放右子树,再放左子树,这样出栈后序列为左右根
if(t->right) stk.push(t->right);
if(t->left) stk.push(t->left);
}
else
{
t = stk.top();
stk.pop();
res.push_back(t->val);
}
}
return res;
}
};
迭代写法三(考研复习资料书):
正常写法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while(root || stk.size())
{
if(root->left)
{
stk.push(root);
root = root->left;
}
else if(root->right)
{
stk.push(root);
root = root->right;
}
else
{
res.push_back(root->val);
while(stk.size())
{
auto t = stk.top();
if(t->left == root && t->right)
{
root = t->right;
break;
}
else
{
stk.pop();
root = t;
res.push_back(root->val);
}
}
}
if(stk.empty()) break;
}
return res;
}
};
173. 二叉搜索树迭代器
本质就是考察二叉树的中序遍历(非递归写法),同94
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class BSTIterator {
public:
stack<TreeNode*> stk;
BSTIterator(TreeNode* root) {
while(root)
{
stk.push(root);
root = root->left;
}
}
int next() {
auto root = stk.top();
stk.pop();
int val = root->val;
root = root->right;
while(root)
{
stk.push(root);
root = root->left;
}
return val;
}
bool hasNext() {
return stk.size();
}
};
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator* obj = new BSTIterator(root);
* int param_1 = obj->next();
* bool param_2 = obj->hasNext();
*/
222. 完全二叉树的节点个数
先判断左右两端点层数是否相同,若相同则是满二叉树,可以用公式算,否则递归左右子树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int countNodes(TreeNode* root) {
if (!root) return 0;
int x = 1, y = 1;
auto l = root->left, r = root->right;
while (l) l = l->left, x ++ ;
while (r) r = r->right, y ++ ;
if (x == y) return (1 << x) - 1;
return countNodes(root->left) + 1 + countNodes(root->right);
}
};
做法,直接遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res = 0;
void dfs(TreeNode* root)
{
if (!root) return;
if (root->left) dfs(root->left);
res ++ ;
if (root->right) dfs(root->right);
}
int countNodes(TreeNode* root) {
dfs(root);
return res;
}
};
230. 二叉搜索树中第K小的元素
方法一:
BST中序遍历是有序的,中序遍历一下输出第k个即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> a;
int res = 0;
int kthSmallest(TreeNode* root, int k) {
if (!root) return 0;
dfs(root);
res = a[k - 1];
return res;
}
void dfs(TreeNode* root)
{
if (root->left) dfs(root->left);
a.push_back(root->val);
if (root->right) dfs(root->right);
}
};
方法二:
维护一个大小为k的大根堆,当堆中元素达到k个后,每次比较当前节点值与堆顶,如果比堆顶小,那么它是更优的解,替换掉堆顶,最后返回堆顶就是答案
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
priority_queue<int> heap;
int k;
int kthSmallest(TreeNode* root, int _k) {
k = _k;
dfs(root);
return heap.top();
}
void dfs(TreeNode* root)
{
if (!root) return;
if (heap.size() < k)
{
// printf("%d被放入堆 ", root->val);
// puts("");
heap.push(root->val);
}
else if (root->val < heap.top())
{
// printf("%d从堆顶弹出,%d变为堆顶", heap.top(), root->val);
// puts("");
heap.pop();
heap.push(root->val);
}
if (root->left) dfs(root->left);
if (root->right) dfs(root->right);
}
};
235. 二叉搜索树的最近公共祖先
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (q->val < p->val) swap(p, q);
if (p->val <= root->val && q->val >= root->val) return root;
if (q->val < root->val) return lowestCommonAncestor(root->left, p, q);
return lowestCommonAncestor(root->right, p, q);
}
};
236. 二叉树的最近公共祖先
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (!root || root == p || root == q) return root;
auto left = lowestCommonAncestor(root->left, p, q);
auto right = lowestCommonAncestor(root->right, p, q);
if (left && right) return root;
if (left) return left;
return right;
}
};
257. 二叉树的所有路径
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<string> res;
vector<int> path;
vector<string> binaryTreePaths(TreeNode* root) {
if (root) dfs(root);
return res;
}
void dfs(TreeNode* root)
{
path.push_back(root->val);
if (!root->left && !root->right)
{
string line = to_string(path[0]);
for (int i = 1; i < path.size(); i ++ )
line += "->" + to_string(path[i]);
res.push_back(line);
}
else
{
if (root->left) dfs(root->left);
if (root->right) dfs(root->right);
}
path.pop_back();
}
};
889. 根据前序和后序遍历构造二叉树

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> pos;
TreeNode* build(vector<int>& preorder, vector<int>& postorder, int a, int b, int x, int y)
{
if (a > b) return NULL;
auto root = new TreeNode(preorder[a]);
if (a == b) return root;
int k = pos[preorder[a + 1]];
root->left = build(preorder, postorder, a + 1, a + 1 + k - x, x, k);
root->right = build(preorder, postorder, a + 1 + k - x + 1, b, k + 1, y - 1);
return root;
}
TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {
int n = preorder.size();
for (int i = 0; i < n; i ++ ) pos[postorder[i]] = i;
return build(preorder, postorder, 0, n - 1, 0, n - 1);
}
};



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 在鹅厂做java开发是什么体验
· 百万级群聊的设计实践
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战
· 永远不要相信用户的输入:从 SQL 注入攻防看输入验证的重要性
· 全网最简单!3分钟用满血DeepSeek R1开发一款AI智能客服,零代码轻松接入微信、公众号、小程