UOJ#37. 【清华集训2014】主旋律

题目大意：

　　传送门

题解：

　　神题……Orz。

　　首先正难则反。

　　设$f_S$表示选取点集状态为s时，这部分图可以构成非强联通图的方案数。

　　设$p_{S,i}$表示点集s缩点后有i个入度为0点的方案数,保证$i<|S|$。

　　设$e[S,T]$表示从S集合到T集合的边数。

　　很显然有。

　　好吧，并不显然……还是来解释一下……

　　考虑求$f_S$，我们知道缩点后必然会有一些点环的入度为0,但数量并不确定，我们强制性的让一部分图构成一部分缩点后为i个入度为0的子图。然后将这部分图随意连向剩余子图，至于剩余子图内部也可以随便连。但是显然当$T==S$时，我们需要让被选择的图缩点后至少要有2个入度为0的点。

　　然后这个东西显然（这次是真的）是会重的，为了去重，我们使用容斥原理，这样我们就得到了上面这玩意。

　　问题是这东西怎么求……

　　我们设。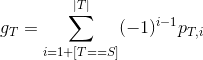

　　值得注意的会发现$g_S$和其他子图不太一样（缩点后有至少两个入度为0的点？）……

　　我们先想这东西怎么搞……

　　先假设已经知道$T\neq S$的$g$值。

　　那么考虑当我们枚举到$T==S$时，由于我们已经将两部分图中连边的方案容斥完了（因为$T==S$时，T不可能再向$S-T$连边）。那么还剩下的就是两部分图中不连边的方案还没有容斥完。（请注意是两部分）

　　为了满足容斥，$g_S$此时应该记录的是分成若干个联通块以后没有边的方案数。

　　这样的话就会导致一个问题$g_S$对于$f_S$和$f_S+I,I\cap S \neq |I|$的意义是不一样的。但$S+I$太遥远了，我们先考虑对于S的意义该怎么算。

　　我们还是可以枚举$S$的子集，我们会得到$g_S=-\sum_T g_T * (2^{e[S-T,S-T]}-f_{S-T})$即我们强制一部图为一个强联通分量，另外一部分图我们使其数量任意。为了使其构成我们想要的意义，那么我们强行不让他们连边。这样我们$S$相对与$T$就多了一个强联通分量，故要乘上$-1$。

　　但这样会出现一个问题，就是我们必然会算重。比如$g_T$中是包含缩成1个点的方案的，$S-T$我们又让它缩成了1个点，这样我们比如会重复计算。当然出重的不只这些。

　　那么为了避免出现这种情况，同时枚举时必然是两个非空子集。那我们就强制让一个点划分到一部分子集里。这样我们就可以解决这个问题了。

　　回来考虑$g_S$对$S+I$该怎么算，我们注意到他们之间的区别是当对于$S$时，我们要求分成至少两个强联通分量，而$S-T$时则可以只有1个，那么我们直接给$g_S$加上$2^{e[S,S]-f_S}$不就完事了。

　　真难表述……(辣鸡linux没有仿宋字体，看得好难受

代码：

#include "bits/stdc++.h"

using namespace std;

inline int read(){
    int s=0,k=1;char ch=getchar();
    while (ch<'0'|ch>'9') ch=='-'?k=-1:0,ch=getchar();
    while (ch>47&ch<='9') s=s*10+(ch^48),ch=getchar();
    return s*k;
}

const int N=20,M=1<<N,mod=1e9+7;

int n,m,S;
int edge[M],num[M],bin[N*N],f[M],g[M],e[M],redge[M],w[M],lgs[M];

int main(){
    //freopen(".in","r",stdin);
    //freopen("vio.out","w",stdout);
    register int i,j,k,res;
    n=read(),m=read();
    for (i=1;i<=m;++i) {
        j=read(),k=read();
        edge[1<<j-1]^=1<<k-1;
        redge[1<<k-1]^=1<<j-1;
    }
    for (i=bin[0]=1;i<=m;++i) j=(bin[i-1]<<1),j<mod?bin[i]=j:bin[i]=j-mod;

    for (S=1<<n,i=1;i^S;++i) num[i]=num[i>>1]+(i&1);    
    for (i=1,lgs[0]=-1;i^S;++i) lgs[i]=lgs[i>>1]+1;
    for (i=1;i^S;++i) j=bin[lgs[i]],e[i]=e[i^j]+num[redge[j]&(i^j)]+num[edge[j]&(i^j)];
    for (i=1;i<S;++i) {
        k=i&-i,res=i^k;
        for (j=res&res-1;j;j=j-1&res) {
            g[i]+=1ll*g[res^j]*(bin[e[j^k]]-f[j^k]+mod)%mod;
            g[i]<mod?0:g[i]-=mod;
        }
        if (num[i]>1) g[i]+=g[res],g[i]<mod?0:g[i]-=mod;        
        g[i]=g[i]?mod-g[i]:0;
        for (j=res;j;j=j-1&i) {
            k=bin[lgs[i^j]];
            w[i^j]=w[i^j^k]+num[redge[k]&j]-num[edge[k]&(i^j^k)];
            f[i]+=1ll*bin[e[i^j]+w[i^j]]*g[j]%mod;
            f[i]<mod?0:f[i]-=mod;
        }
        f[i]+=g[i];
        f[i]<mod?0:f[i]-=mod;
        g[i]+=(bin[e[i]]-f[i]+mod)%mod;
        g[i]<mod?0:g[i]-=mod;
    }
    printf("%d\n",(bin[m]-f[S-1]+mod)%mod);
    return 0;
}