【BZOJ 3569】 DZY Loves Chinese II

题目连接：

　　传送门

题解：

　　先%一发大佬的题解。

　　考虑一个图，删除一些边以后不连通的条件为，某个联通块与外界所有连边都被删掉，而不只是生成树中一个树边与所以覆盖它的非树边（很容易举出反例）。

　　那么考虑如何才能判断一个联通块与外界隔断。

　　先考虑只是一棵树，那么任意割一条边都成立，那么现在我们在这棵树上加上一条边(u,v)，我们发现，在(u,v)以外的树边，割一条就成立，但在（u,v）覆盖以内呢？

　　如图：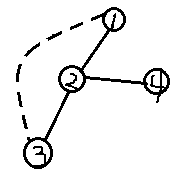　　

　　我们发现我们可以把（u,v）与被（u,v）覆盖的任意一条边删掉，但也可以把2向外连出，且被（u,v）覆盖的边给删掉（即(1,2)、（2，3））。当我们把（2）看作一团点时我们可以发现以上条件也是成立的。

　　以此类推我们可以发现被覆盖的树边删除后不再联通的条件为：1.删除其本身，同时将覆盖其的边删掉；2.删除其本身，将与其一同被覆盖的其他树边删掉。

　　也就是说，产生新联通块的必要条件为：删掉一条树边的同时，与其具有相同属性的边也被删掉。

　　那么这个相同属性是什么：覆盖边的属性。我们用一个数来表示覆盖边的属性，也就是说我们删除的集合要满足删除边的属性异或和为0，同时不能为空集！

　　还是如上图，我们把（1，3）的边用x表示，我们给（2，3）、（1，2），即被覆盖边都打上x的标记，那么我们发现删除这三者中的任意二者都是成立的，因为x这个属性，被gank了两次，也就意味着这个覆盖边的贡献在我们删掉的边之间的联通块（假想块），与覆盖边以外的联通块隔离。

　　所以我们随机一个数给非树边作为它的属性，那么删边形成新联通的条件就是删边集合中，存在一个子集（不含空集）的属性异或和为0。

代码：

#include "bits/stdc++.h"

using namespace std;

inline int read() {
    int s=0,k=1;char ch=getchar();
    while (ch<'0'|ch>'9') ch=='-'?k=-1:0,ch=getchar();
    while (ch>47&ch<='9') s=s*10+(ch^48),ch=getchar();
    return s*k;
}

const int N=5e5+10,mod=1e9;

struct edges{
    int v;edges *last;
}edge[N*2],*head[N];int cnt=1;

inline void push(int u,int v){
    edge[++cnt]=(edges){v,head[u]},head[u]=edge+cnt;
}

struct node {
    int x,y,val;
}ed[N];

bool vis[N],used[N];int fat[N],val[N];

inline void dfs(int x,int fa){
    vis[x]=true;
    for (edges *i=head[x];i;i=i->last)  if(i->v!=fa&&!vis[i->v]){
        fat[i->v]=x;used[i-edge>>1]=true;  
        dfs(i->v,x);
    }
}

inline void dfs2(int x,int fa){
    for (edges *i=head[x];i;i=i->last)  if(fat[i->v]==x){
        dfs2(i->v,x);
        val[x]^=val[i->v];
        ed[i-edge>>1].val^=val[i->v];
    }
}

int n,m,b[40],bin[40];

int main() {
    srand(20000820);
    n=read(),m=read();
    register int i,j,k;
    for (i=1;i<=m;++i)  ed[i].x=read(),ed[i].y=read(),push(ed[i].x,ed[i].y),push(ed[i].y,ed[i].x);
    dfs(1,0);
    for (i=1;i<=m;++i)  if(!used[i]){
        int x=1ll*rand()*rand()%mod+1;        
        ed[i].val=x;
        val[ed[i].x]^=x;
        val[ed[i].y]^=x;
    }
    dfs2(1,0);
    int Q=read(),num,x,ans=0;
    for (i=0;i<=30;++i) bin[i]=1<<i;
    while (Q--){
        num=read();
        memset(b,0,sizeof(b));
        bool flag=true;
        for (i=1;i<=num;++i){
            x=read()^ans;x=ed[x].val;
            for (j=30;~j;--j)   if(x&bin[j]){
                if(b[j])    x^=b[j];
                else    {
                    b[j]=x;
                    for (k=j-1;~k;--k)  if(b[k]&&(bin[k]&b[j])) b[j]^=b[k];
                    for (k=j+1;j<=30;++j)   if(b[k]&bin[j]) b[k]^=b[j];
                    break;
                }
            }
            if(x==0)   flag=false; 
        }
        ans+=flag;
        puts(flag?"Connected":"Disconnected");
    }
}