线性基学习笔记
如果有线性代数基础的话会更易理解。推荐配合本人的线性代数学习笔记食用。
线性基是针对某个序列生成的一个集合，它具有以下两条性质：
-
线性基中任意选择一些数的异或值所构成的集合，等于原序列中任意选择一些数的异或值所构成的集合。
-
线性基是满足上述条件的最小集合。
有了上面这两条性质，我们便可以得出如下几条推论：
-
原序列中任何数，都可以由线性基中一些数异或起来得到（由性质1直接得出）
-
线性基中不存在一组数，使得它们的异或值为\(0\)（如果存在\(x\operatorname{xor}y\operatorname{xor}z=0\)，它就等价于\(x\operatorname{xor}y=z\)，就可以删掉\(z\)使得异或集合不变，违背了性质2）
-
线性基中不存在两组取值集合，使得它们的异或和相等（不然你把这两个集合异或在一起就会得到异或和为\(0\)的集合）
现在介绍线性基的构建方法：
我们用\(x_{(2)}\)表示\(x\)的二进制表示，用\(d_x\)表示线性基数组。
\(d_x\)具有如下性质：
当\(d_x\)不为\(0\)时，表明这一位上储存了一个线性基。
\((d_x)_{(2)}\)的第\(x\)位一定为\(1\)，且第\(x+1\)位往后全都为\(0\)。
这是它的构造方式（向序列中插入一个数\(x\)）：
void ins(ll x){
for(int i=55;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];//eliminate the 1 on the i-th bit of x
else{d[i]=x;break;}//successfully inserted, jump out.
}
}
这是什么意思呢？
我们要尽量把\(x\)异或到\(0\)，因为一旦异或到\(0\)就表明\(x\)可以被线性基表示出来，就不用加入线性基了。
如果\(x\)的第\(i\)位是\(0\)，你要这时候异或上去了\(d_i\)，它的第\(i\)位就是\(1\)了，这个\(1\)以后消不掉（\(i\)是\(d_i\)的最高位），故直接跳掉。
如果\(x\)的第\(i\)位是\(1\)，这时候必须异或上\(d_i\)才能消掉这一位（以后消不掉），不管对之后位数的影响。
那如果这时的\(d_i\)不存在呢？很显然这时\(x\)不能被线性基中的数表示出来，因此要把\(x\)加入线性基。
那什么时候这个\(x\)不会被加入线性基呢？很显然，当某次异或之后，\(x\)变成了\(0\)。则此时\(x\)可以被集合中数表示出来，可以不加入。
这就是构建线性基的方式。
注意数据范围！当它是long long范围时，记得写1ll<<x而非1<<x！
很明显，构造线性基的复杂度是\(O(n\log a_i)\)的，其中\(n\)为插入数的个数，\(a_i\)为插入的数。
但是，当\(a_i\)很大（比如说\(2^{1000}\)级别）的时候，你就不得不使用bitset来代替，此时复杂度就是\(O(n\dfrac{\log^2a_i}{w})\)，其中\(w\)是bitset常数。bitset具体的实现在我们接下来的例题4.3.[[HAOI2017]八纵八横]中可以看到。
一般不会有毒瘤出题人卡线性基时间复杂度的，毕竟（位运算/bitset+循环）让它的效率极高，并且它也没有过多变形（不像线段树什么的），所以一般不用担心复杂度。
更多操作随着例题会逐步解锁。
Part1. 线性基基础操作
I.求\(\max\)异或值（即【模板】线性基）
从高位往低位枚举\(d_i\)，维护一个答案\(res\)。如果\(res\)异或上\(d_i\)更优，则异或。
显然，如果\(res\)的第\(i\)位是\(1\)，这时肯定不会异或——不然就把这个\(1\)给消去了，而就算之后的位上全是\(1\)，也抵不上这里的一个\(1\)（考虑类比01trie的贪心）。
而如果这位上是\(0\)，则一定要异或上\(d_i\)将这位变成\(1\)。
因此最终呈现出来的结果就是能异或就异或。（注意异或的优先级是要劣于小于号的优先级的，故记得加括号）
代码：
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll a[100],d[100],res;
void ins(ll x){
for(int i=55;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];//eliminate the 1 on the i-th bit of x
else{d[i]=x;break;}//successfully inserted, jump out.
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]),ins(a[i]);
for(int i=55;i>=0;i--)if((res^d[i])>res)res^=d[i];
printf("%lld\n",res);
return 0;
}
II.求\(\min\)异或值
显然，当某次插入失败时，答案即为\(0\)。（因为插入失败即意味着存在一些数，其异或值为 \(0\)）
而当没有任何插入失败时，答案为\(\min\{d_i\}\)（这点可以在我们接下来的\(k\)小异或和中看得更清楚）
III.求第\(k\)小异或和（即LOJ#114.k大异或和）
我们首先建出线性基出来。
注意到线性基是非唯一的——我们随便拿线性基中任意两个数异或到一起，就可以得到新的一组线性基。换句话说，线性基具有异或等价性。
而在这所有线性基中，我们这里要用的便是所有\(d_x\)最小的那一组。
构造方法很简单——从小到大枚举所有\(d_i\)，从大到小枚举所有\(j<i\)，如果\(d_i\operatorname{xor}d_j<d_i\)，就\(\operatorname{xor}\)掉。这个性质可以通过贪心加以理解——对于 \(d_i\)，其二进制下最高位是 \(i\)，而无论 \(d_i\) 与哪个 \(d_j\)——其中 \(j>i\)——加以异或，总会在比 \(i\) 更高的一位上出现 \(1\)，一定更劣。而，从大往小地枚举 \(j<i\)，可以保证如果 \(d_i\) 的第 \(j\) 位上是 \(1\)，贪心地异或掉一定更优，并且这一位不会在后面的过程中重新被异或成 \(1\)。
在这里，我们就可以看出\(\min\)异或值为什么是\(\min\{d_i\}\)了：因为\(\min\{d_i\}\)即是\(i\)最小的那个\(d_i\)，它不存在一个\(j\)可以跟它异或，故它的值不会变化，一直是最小值。
这么全部搞完之后，我们得到一组新的线性基。这组线性基具有一个性质：对于 \(i\)，\(d_i\) 是 \(d\) 数组中唯一一个在第 \(i\) 位上有 \(1\) 的数。这个性质可以直接由构造过程得出。
然后，考虑任意一组集合 \(\{d_{x_1},d_{x_2},\dots,d_{x_m}\}\)，其异或起来会得到一个值。假设我们现在选择了一个未出现过的 \(d_i\) 加入集合，则因为当前集合中任意一个数中第 \(i\) 位均为 \(0\)，则异或结果第 \(i\) 位也为 \(0\)，现在异或上一个 \(d_i\)，第 \(i\) 位由 \(0\) 变 \(1\)，而更高位没有变化，于是结果一定更大。所以，这个线性基中的数是越异或越大的，不会出现一个数异或上一个新数后反而变小的情况。
同时，前 \(i-1\) 个 \(d_i\) 中任意多个数的异或和小于 \(d_i\)，这是仍然成立的。
则，我们考虑设所有非零的 \(d_i\) 依次构成集合 \(\{t_0,t_1,\dots\}\)。考虑所有可能出现的数所构成的集合，则最小的一定是 \(t_0\)，因为其它任何东西相比它都在更高位上有数；次小的一定是 \(t_1\)，因为所有包含 \(t_i(i>1)\) 的取值集合一定比它大，所以次小的结果一定只能在 \(t_1\) 或 \(t_0\text{ xor }t_1\) 中出现；根据我们前面的推论，更小的一定是 \(t_1\)。同时，我们还可以得到三小的是 \(t_0\text{ xor }t_1\)。第四小，因为 \(1\) 往下的东西全取过了，所以只能选 \(t_2\)；第五小，其在 \(t_2\text{ xor }t_1\) 和 \(t_2\text{ xor } t_0\) 中出现。我们会发现，所有比 \(t_1\) 最高位更高的位在二者中并无区别，而 \(t_1\) 的最高位，在前者中为 \(1\)（因为 \(t_2\) 的这一位，依照我们前面的推论，一定是 \(0\)），在后者中是 \(0\)，则后者一定更小。同时，我们发现第六小是 \(t_2\text{ xor }t_1\)……
等等等等，我们有没有发现，上述过程中，第一小是 \(t_0\)，第二小是 \(t_1\)，第三小是 \(t_{0,1}\)，四小是 \(t_2\)，五小是 \(t_{0,2}\)，六小是 \(t_{1,2}\)……
这恰恰是 \(0\sim5\) 的二进制表达上的非零位！类似的规律是否对于更大的值也存在呢？
事实上，是成立的。可以采取数学归纳法简单理解一下：设第 \(x\) 大的表达是 \(t_{x_0}\text{ xor }t_{x_1}\text{ xor }t_{x_2}\text{ xor}\dots\)。现在考虑第 \(x+1\) 大。显然，如果 \(t_0\) 未出现，异或上它得到的结果一定是最小的；否则，若 \(t_1\) 未出现，则 \(t_1\) 是一定要被异或上才能使结果增大的；而此时，撤去 \(t_0\) 会使得结果稍稍减小（\(t_0\) 最高位的元素由 \(1\) 转 \(0\)），但是仍然比第 \(x\) 大的数要大；所以，此时应撤去 \(t_0\) 换成 \(t_1\)，刚好是 \(x\) 加一后其二进制上的变化。更大位数上的变化，也可以类似地证明。
（事实上，还有一种感性的理解方式是将所有的 \(d_i\) 就看作其最高位，最高位更大就一切更大，这样理解会要简单得多）
因此我们只需要求出从小到大所有的不为\(0\)的\(d_i\)，记其数量为\(tot\)。如果\(tot\neq n\)，就意味着有数插入线性基失败，存在一个\(0\)作为异或和，\(k\)应该减一；然后，如果\(k\geq 2^{tot}\)，就意味着全部异或和数量小于\(k\)，输出\(-1\)；否则，找出\(k_{(2)}\)中所有非\(0\)位，计算对应位置（指第\(x\)个非零的线性基）的\(d_x\)的异或和即可。
代码：
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,d[64],arr[64],tot;
void ins(int x){
for(int i=55;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
void rebuild(){
for(int i=0;i<=55;i++)for(int j=i-1;j>=0;j--)if(d[i]&(1ll<<j))d[i]^=d[j];
for(int i=0;i<=55;i++)if(d[i])arr[tot++]=i;
}
signed main(){
scanf("%lld",&n);
for(int i=1,x;i<=n;i++)scanf("%lld",&x),ins(x);
rebuild(),scanf("%lld",&m);
for(int i=1,x,res;i<=m;i++){
scanf("%lld",&x),res=0;
if(tot<n)x--;
if(x>=(1ll<<tot)){puts("-1");continue;}
for(int j=0;j<tot;j++)if(x&(1ll<<j))res^=d[arr[j]];
printf("%lld\n",res);
}
return 0;
}
IV.线性基合并（即[SCOI2016]幸运数字）
题解区用点分治的、用树剖的是什么神仙啦，这题根本不需要呀
线性基具有可并性，即你可以合并两块线性基得到一块更大的线性基，合并方式是将一块线性基中所有东西暴力插入另一块，复杂度\(O(\log^2)\)。
于是我们便很轻松地可以把线性基模板化掉：
struct lb{//linear basis?
ll d[64];
void print(){
for(int i=0;i<=62;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
ll& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=62;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=62;i>=0;i--)if(y[i])z+=y[i];
return z;
}
ll calc(){//calculate maximum possible
ll res=0;
for(int i=62;i>=0;i--)if((res^d[i])>res)res^=d[i];
return res;
}
};
回到这道题。首先，关于路径，肯定会想到求LCA，而求LCA的方法之一便是倍增。因此我们只需要预处理倍增线性基即可在求LCA的同时求出线性基了。
复杂度\(O(n\log^3n)\)。
代码：
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,anc[20100][16],dep[20100];
ll val[20100];
struct lb{//linear basis?
ll d[64];
void print(){
for(int i=0;i<=62;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
ll& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=62;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=62;i>=0;i--)if(y[i])z+=y[i];
return z;
}
ll calc(){
// print();
ll res=0;
for(int i=62;i>=0;i--)if((res^d[i])>res)res^=d[i];
return res;
}
}LB[20100][16];
vector<int>v[20100];
void dfs(int x){
LB[x][0]+=val[x];
for(int y:v[x])if(y!=anc[x][0])dep[y]=dep[x]+1,anc[y][0]=x,dfs(y);
}
ll query(int x,int y){
lb z;
if(dep[x]<dep[y])swap(x,y);
for(int i=15;i>=0;i--)if(dep[x]-(1<<i)>=dep[y])z+=LB[x][i],x=anc[x][i];
if(x==y){z+=val[x];return z.calc();}
for(int i=15;i>=0;i--)if(anc[x][i]!=anc[y][i])z+=LB[x][i],z+=LB[y][i],x=anc[x][i],y=anc[y][i];
z+=LB[x][0];
z+=LB[y][0];
z+=val[anc[x][0]];
return z.calc();
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%lld",&val[i]);
for(int i=1,x,y;i<n;i++)scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
dfs(1);
for(int j=1;j<=15;j++)for(int i=1;i<=n;i++)anc[i][j]=anc[anc[i][j-1]][j-1],LB[i][j]=LB[i][j-1]+LB[anc[i][j-1]][j-1];
for(int x,y;m--;)scanf("%d%d",&x,&y),printf("%lld\n",query(x,y));
return 0;
}
Part2.线性基上排序与贪心
I.[BJWC2011]元素
还记得我们之前说的吗？
性质2.线性基是满足上述条件的最小集合。
推论4.线性基中不存在一组数，使得它们的异或值为0
则我们发现，一组符合条件的矿石，必然构成线性基（最大，因为如果还有数可以被加入集合，则加入一定更优；不存在 \(0\)，由定义直接得到）。
考虑当我们新加入一个数时，设为 \(x\)，如果插入成功，则插入；否则，即插入失败，则当前线性基中一定有且仅有一组东西能够直接表示出 \(x\)，不妨设 \(\text{xor }t_i=x\)。则，\(x\) 可以置换出 \(t_i\) 中任何一个数，使得仍构成线性基。显然，贪心地想，我们一定要置换掉最小的数。则，假如 \(t\) 中最小的数比 \(x\) 小，则置换即可。
显然，任意多次操作后，任意初始线性基得到的集合都是相同的——因为线性基中所有元素会在置换的过程中总体不降，所以最终得到的一定是最大的一组。
在实际应用中，我们没有必要真正模拟置换的过程——只需要把所有元素从大到小排序后加入线性基，这样置换便不可能发生，于是所得到的线性基就直接是最大的一组了。
代码：
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,res;
ll d[100];
bool ins(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;return true;}
}
return false;
}
pair<int,ll>p[1010];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lld%d",&p[i].second,&p[i].first);
sort(p+1,p+n+1);
for(int i=n;i;i--)if(ins(p[i].second))res+=p[i].first;
printf("%d\n",res);
return 0;
}
II.[CQOI2013] 新Nim游戏
回忆起NIM游戏先手必胜当且仅当所有石子堆的异或和不为\(0\)。
我们可以发现，这题先手必然必胜——因为先手第一次总是可以取到只剩一堆石子，然后后手第一次就什么也取不了，然后先手第二次就可以直接取掉剩下那一堆。
从上面那个思路中，我们发现先手的目标肯定是去掉一些数，使得剩下的数不存在异或和为\(0\)的非空子集。不然，对手肯定就直接把除了那个非空子集外其它东西全部取光，先手就必败了。
不存在异或和为\(0\)的非空子集，这好像意味着序列中所有数都可以被插入一个线性基！
因此我们就直接照着2.1.[BJWC2011]元素，排序后插入线性基即可。
代码：
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,a[110],d[110];
ll res;
bool ins(ll x){
for(int i=31;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;return true;}
}
return false;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
sort(a+1,a+n+1);
for(int i=n;i;i--)if(!ins(a[i]))res+=a[i];
printf("%lld\n",res);
return 0;
}
Part3.每个异或值出现了多少次
I.[TJOI2008]彩灯
那个“亮变暗，暗变亮”刚好是异或的定义。
在建出线性基后，我们翻到开头，有：
性质1.线性基中任意个数的异或值所构成的集合，等于原序列中任意个数的异或值所构成的集合。
推论5.线性基中不存在两组取值集合，使得它们的异或和相等
这就意味着线性基中总共\(2^{tot}\)种取值，就刚好等于原数组的所有异或值的可能。
因此答案即为\(2^{tot}\)。
代码：
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,tot;
ll d[100];
char s[100];
void ins(){
ll x=0;
for(int i=0;i<n;i++)x=(x<<1)+(s[i]=='O');
for(int i=n-1;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x,tot++;break;}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%s",s),ins();
printf("%lld\n",(1ll<<tot)%2008);
return 0;
}
II.albus就是要第一个出场
打开这题，我们发现它和LOJ#114.k大异或和长得惊人的类似，就是一个是求排第几的是谁，一个是求它排第几而已。
这种位置和次序互相转换的题，一般来说套个二分就能解决。
但是这里的集合是可重集，咋办呢？
没关系！我们之前一开始得出了一条推论：
推论5.线性基中不存在两组取值集合，使得它们的异或和相等。
而我们可以把所有加入线性基失败的数看作\(0\)（之前说过，线性基内部任意两个数互相异或得到的新集合仍然是一组线性基；如果把加入失败的数也看做加入了线性基，则多次异或后最终可以看作是\(0\)）。
则原序列的集合中所有数都出现了\(2^{n-tot}\)次（因为一共有\(n-tot\)个\(0\)，从中选出任意多个异或在一起仍然是\(0\)，再跟另一个数异或起来，就会发现每个数都出现了\(2^{n-tot}\)次）。
故我们直接套上二分后答案乘上\(2^{n-tot}\)即可。
代码：
#include<bits/stdc++.h>
using namespace std;
const int mod=10086;
int n,m,d[40],arr[40],tot;
void ins(int x){
for(int i=31;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
void rebuild(){
for(int i=0;i<=31;i++)for(int j=i-1;j>=0;j--)if(d[i]&(1<<j))d[i]^=d[j];
for(int i=0;i<=31;i++)if(d[i])arr[tot++]=i;
}
int query(int ip){
int res=0;
for(int i=tot-1;i>=0;i--)if(ip&(1<<i))res^=d[arr[i]];
return res;
}
int ksm(int x,int y){
int z=1;
for(;y;x=1ll*x*x%mod,y>>=1)if(y&1)z=1ll*x*z%mod;
return z;
}
signed main(){
scanf("%d",&n);
for(int i=1,x;i<=n;i++)scanf("%d",&x),ins(x);
rebuild();
scanf("%d",&m);
int l=0,r=(1<<tot)-1;
while(l<r){
int mid=(l+r+1)>>1;
if(query(mid)<=m)l=mid;
else r=mid-1;
}
printf("%d\n",(1ll*ksm(2,n-tot)*l+1)%mod);
return 0;
}
III.CF959F Mahmoud and Ehab and yet another xor task
这名字真长
可以发现这题实际上和上题类似，仍然只是求出\(2^{n-tot}\)即可。
但是这道题是多组询问，还是针对前缀的！
这里就有两种方法：
-
离线下来，然后一遍扫过即可。
-
可持久化线性基。
不要以为是什么高大上的东西，可持久化线性基就直接copy一遍数组即可，复杂度\(O(n\log a_i)\)，因为你求线性基的时候总是免不了遍历一遍数组的。
代码（离线做法）：
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int n,m,a[100100],d[30],res[100100],tot,pov[100100];
bool ins(int x){
for(int i=22;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;return true;}
}
return false;
}
bool find(int x){
for(int i=22;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else return false;
}
return true;
}
vector<pair<int,int> >v[100100];
int main(){
scanf("%d%d",&n,&m),pov[0]=1;
for(int i=1;i<=n;i++)scanf("%d",&a[i]),pov[i]=(pov[i-1]<<1)%mod;
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),v[x].push_back(make_pair(y,i));
for(int i=1;i<=n;i++){
tot+=ins(a[i]);
for(auto j:v[i])res[j.second]=pov[i-tot]*find(j.first);
}
for(int i=1;i<=m;i++)printf("%d\n",res[i]);
return 0;
}
IV.CF895C Square Subsets
听说这题有用状压的神仙，orzorz
首先，因为\(a_i\)的范围很小（\(70\)），我们可以很轻松地想到要与\(a_i\)范围内的质数有关。
人脑枚举一下后，我们发现\(70\)以内的质数有：
\(2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67\)，共\(19\)个。
因为最终的乘积为完全平方数，当且仅当每个质数在乘积中出现了偶数次，所以我们可以很轻松地把每个\(a_i\)转成每个质数出现了奇数次还是偶数次的一个bitmask。
发现两个数乘在一起，就相当于把它们的bitmask异或起来。则只有一堆数的bitmask的异或和为\(0\)，它们的积才是完全平方数。这不就是前几题的内容吗？
然后直接把它丢入线性基，则答案即为\(2^{n-tot}-1\)（这题不能选空集）。
另外还有一道双倍经验的题是ACMSGURU 200. Cracking RSA ，只不过那题的答案可能爆long long，CF又不给用__int128，故只能用两个unsigned long long来模拟___int128。
代码（CF895C的，双倍经验那题只需要换成bitset然后再把答案用两个ull装就行了）：
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int n,pri[22]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67},tot,pov[100100],d[20];
bool ins(int x){
for(int i=20;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;return true;}
}
return false;
}
int main(){
scanf("%d",&n),pov[0]=1;
for(int i=1,x,y;i<=n;i++){
scanf("%d",&x),y=0;
for(int j=0;j<19;j++){
if(x%pri[j])continue;
int z=0;
while(!(x%pri[j]))x/=pri[j],z^=1;
y|=(z<<j);
}
tot+=ins(y);
pov[i]=(pov[i-1]<<1)%mod;
}
printf("%d\n",pov[n-tot]-1);
return 0;
}
V.TopCoder13145-PerfectSquare
和前几题类似。我们仍然选择将每个数质因数分解，然后将其转换为一个 01 串。
然而这题还有一个限制，即每行每列都只能取奇数个东西。
于是我们额外在每个 01 串前面添上 \(2n\) 位，表示当前的元素位于哪一行哪一列，然后建出线性基。最后，只要查询除了前 \(2n\) 位是 \(1\)，其它位都是 \(0\) 的串是否在线性基内出现，且出现了多少次即可。
代码：
#include<bits/stdc++.h>
using namespace std;
const int lim=40000;
const int LEN=1020;
const int mod=1e9+7;
#define BIT bitset<LEN>
class PerfectSquare{
private:
int a[30][30],n,m,nul;
BIT bs[LEN];
map<int,int>mp;
int pri[40100];
void Eular(){
for(int i=2;i<=lim;i++){
if(!pri[i])pri[++pri[0]]=i;
for(int j=1;j<=pri[0]&&i*pri[j]<=lim;j++){
pri[i*pri[j]]=true;
if(!(i%pri[j]))break;
}
}
}
void ins(BIT &x){
for(int i=m-1;i>=0;i--){
if(!x[i])continue;
if(bs[i][i])x^=bs[i];
else{bs[i]=x;return;}
}
nul++;
}
bool find(BIT &x){
for(int i=m-1;i>=0;i--){
if(!x[i])continue;
if(bs[i][i])x^=bs[i];
}
return x.none();
}
public:
int ways(vector<int>v){
n=sqrt(v.size())+0.1,Eular();
for(int i=0;i<n;i++)for(int j=0;j<n;j++)a[i][j]=v[i*n+j];
m=2*n;
for(int i=0;i<n;i++)for(int j=0;j<n;j++){
BIT x;
x[i]=true,x[n+j]=true;
for(int k=1;k<=pri[0];k++){
if(a[i][j]%pri[k])continue;
if(!mp[pri[k]])mp[pri[k]]=m++;
while(!(a[i][j]%pri[k]))x.flip(mp[pri[k]]),a[i][j]/=pri[k];
}
if(a[i][j]!=1){
if(!mp[a[i][j]])mp[a[i][j]]=m++;
x.flip(mp[a[i][j]]);
}
ins(x);
}
BIT x;
for(int i=0;i<2*n;i++)x[i]=true;
if(!find(x))return 0;
int ret=1;
for(int i=0;i<nul;i++)(ret<<=1)%=mod;
return ret;
}
}my;
Part4.线性基在图论方面的应用
I.[WC2011]最大XOR和路径
就我一个人一开始只想到二进制分解按位处理然后没写出来吗
显然，这题的路径不是简单路径，它可以有重点重边。但是，如果我们对于所有边求异或和的话，你会惊奇的发现有贡献的边只有一条从\(1\)到\(n\)的主路径和许多环！
我们可以看一张图：
路径上的红边都经过了一次，而蓝边却经过了两次，被消掉了！
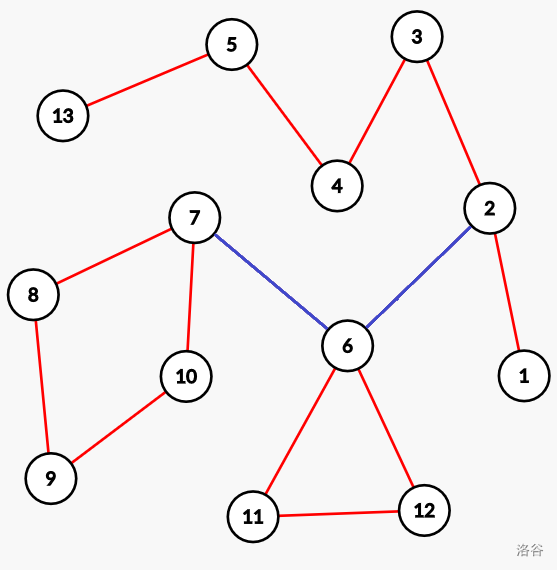
所以我们可以先一遍dfs求出所有环的异或和丢入线性基，然后再用一条\(1\rightarrow n\)的路径的异或和从中找到最大异或和即可。
至于找哪条路径呢？随便找，反正任何两条\(1\rightarrow n\)的路径都会构成一个环，在线性基里如果更优就被异或掉了。
代码：
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,head[50100],cnt;
ll dis[50100];
struct lb{//linear basis?
ll d[64];
void print(){
for(int i=0;i<=62;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
ll& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=62;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=62;i>=0;i--)if(y[i])z+=y[i];
return z;
}
ll calc(ll x){//calculate maximum possible
ll res=x;
for(int i=62;i>=0;i--)if((res^d[i])>res)res^=d[i];
return res;
}
}LB;
struct node{
int to,next;
ll val;
}edge[200100];
void ae(int u,int v,ll w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
bool vis[50100];
void dfs(int x){
for(int i=head[x];i!=-1;i=edge[i].next){
if(!vis[edge[i].to])vis[edge[i].to]=true,dis[edge[i].to]=dis[x]^edge[i].val,dfs(edge[i].to);
else LB+=dis[x]^dis[edge[i].to]^edge[i].val;
}
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(ll i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(x,y,z);
dfs(1);
printf("%lld\n",LB.calc(dis[n]));
return 0;
}
II.CF845G Shortest Path Problem?
嗯，这题跟上一题一样，就是上题是求\(\max\)，这题是求\(\min\)。
在线性基中寻找最小异或和（不是1.2中那个，因为这题是找关于\(1\rightarrow n\)路径异或和的最小异或和），就跟最大异或和一样——从高位到低位枚举\(d_i\)，假如异或起来更小，就异或掉。这也是贪心的道理。
代码：
#include<bits/stdc++.h>
using namespace std;
int n,m,head[100100],cnt,dis[100100];
struct lb{//linear basis?
int d[40];
void print(){
for(int i=0;i<=30;i++)if(d[i])printf("%d:%d\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(int x){
for(int i=30;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
int& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=30;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=30;i>=0;i--)if(y[i])z+=y[i];
return z;
}
int calc(int x){//calculate minimum possible
int res=x;
for(int i=30;i>=0;i--)if((res^d[i])<res)res^=d[i];
return res;
}
}LB;
struct node{
int to,next,val;
}edge[200100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
bool vis[100100];
void dfs(int x){
for(int i=head[x];i!=-1;i=edge[i].next){
if(!vis[edge[i].to])vis[edge[i].to]=true,dis[edge[i].to]=dis[x]^edge[i].val,dfs(edge[i].to);
else LB+=dis[x]^dis[edge[i].to]^edge[i].val;
}
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),ae(x,y,z);
dfs(1);
// LB.print();
printf("%d\n",LB.calc(dis[n]));
return 0;
}
III.[HAOI2017]八纵八横
在这题，我们将会介绍可删除线性基，离线和在线两种做法。因为篇幅有点长，可以参见笔者的题解，此处不再赘述。
IV.CF938G Shortest Path Queries
请务必先把前一道题的题解看完——在那里面介绍的可删除线性基，是我们这题仍然需要用的。
在那篇题解中，我还用LCT维护动态图的连通性来类比了可删除线性基，然后这题我们就真的要来用LCT维护了！
不会LCT的可以左转LCT学习笔记，不知道怎么维护连通性的参见该笔记的XVI.二分图 /【模板】线段树分治。
我们这题就要用LCT先来维护连通性。因为在上一题中，“公路”是永远不会被删除的，我们求出两点间距离可以直接使用公路的结果，所以上一题不需要LCT；但是这题没有一棵始终存在的生成树，只保证它始终联通，故为了求出两点间距离，我们需要使用LCT。
因为LCT和线性基中维护的都是何时这条边/这个线性基会被删除，所以可以很方便地嫁接在一起，只需要在成环时将环的异或值加入线性基即可。复杂度\(O(n\log n)\)。
代码：
#include<bits/stdc++.h>
using namespace std;
int n,m,q,qwq;
pair<int,int>p[200100];
struct edge{
int x,y,z,st,ed;
}e[400100];
//-----------------------Linear Basis Below----------------
int tms[40],d[40];
void ins(int now,int x){
for(int i=30;i>=0;i--){
if(!(x&(1<<i)))continue;
if(tms[i]<now)swap(tms[i],now),swap(x,d[i]);
if(!now)break;
x^=d[i];
}
}
int ask(int now,int x){
for(int i=30;i>=0;i--)if(tms[i]>now&&(x^d[i])<x)x^=d[i];
return x;
}
void print(){
for(int i=0;i<=30;i++)if(d[i])printf("%d:%d\n",i,d[i]);
}
//------------------Linear Basis Above---------------------
//------------------LCT Below------------------------------
#define lson t[x].ch[0]
#define rson t[x].ch[1]
struct LCT{
int fa,ch[2],mn,del,sum,val;
bool rev;
}t[600100];
inline int identify(int x){
if(x==t[t[x].fa].ch[0])return 0;
if(x==t[t[x].fa].ch[1])return 1;
return -1;
}
inline void pushup(int x){
t[x].mn=x;
t[x].sum=t[x].val;
if(lson){
if(t[t[x].mn].del>t[t[lson].mn].del)t[x].mn=t[lson].mn;
t[x].sum^=t[lson].sum;
}
if(rson){
if(t[t[x].mn].del>t[t[rson].mn].del)t[x].mn=t[rson].mn;
t[x].sum^=t[rson].sum;
}
}
inline void REV(int x){
t[x].rev^=1,swap(lson,rson);
}
inline void pushdown(int x){
if(!t[x].rev)return;
if(lson)REV(lson);
if(rson)REV(rson);
t[x].rev=0;
}
inline void rotate(int x){
register int y=t[x].fa;
register int z=t[y].fa;
register int dirx=identify(x);
register int diry=identify(y);
register int b=t[x].ch[!dirx];
if(diry!=-1)t[z].ch[diry]=x;t[x].fa=z;
if(b)t[b].fa=y;t[y].ch[dirx]=b;
t[y].fa=x,t[x].ch[!dirx]=y;
pushup(y),pushup(x);
}
inline void pushall(int x){
if(identify(x)!=-1)pushall(t[x].fa);
pushdown(x);
}
inline void splay(int x){
pushall(x);
while(identify(x)!=-1){
register int fa=t[x].fa;
if(identify(fa)==-1)rotate(x);
else if(identify(x)==identify(fa))rotate(fa),rotate(x);
else rotate(x),rotate(x);
}
}
inline void access(int x){for(register int y=0;x;x=t[y=x].fa)splay(x),rson=y,pushup(x);}
inline void makeroot(int x){access(x),splay(x),REV(x);}
inline int split(int x,int y){makeroot(x),access(y),splay(y);return t[y].sum;}
inline void link(int x,int y){makeroot(x),t[x].fa=y;}
inline void cut(int x,int y){split(x,y),t[y].ch[0]=t[x].fa=0,pushup(y);}
inline int findroot(int x){
access(x),splay(x);
pushdown(x);
while(lson)x=lson,pushdown(x);
splay(x);
return x;
}
inline void LINK(int ip){
t[ip+n].val=e[ip].z;
t[ip+n].del=e[ip].ed;
pushup(ip+n);
if(findroot(e[ip].x)!=findroot(e[ip].y)){link(e[ip].x,ip+n),link(e[ip].y,ip+n);return;}
split(e[ip].x,e[ip].y);
int id=t[e[ip].y].mn;
if(t[id].del>t[ip+n].del){ins(t[ip+n].del,t[e[ip].y].sum^t[ip+n].val);return;}
cut(e[id-n].x,id),cut(e[id-n].y,id);
link(e[ip].x,ip+n),link(e[ip].y,ip+n);
ins(t[id].del,split(e[id-n].x,e[id-n].y)^t[id].val);
}
//-----------------LCT above-------------------------------
map<pair<int,int>,int>mp;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)t[i].del=0x3f3f3f3f,t[i].val=0;
for(int i=1;i<=m;i++)scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z),mp[make_pair(e[i].x,e[i].y)]=i;
scanf("%d",&q);
for(int i=1,tp,x,y,z;i<=q;i++){
scanf("%d%d%d",&tp,&x,&y);
if(tp==1)scanf("%d",&z),++m,e[m].x=x,e[m].y=y,e[m].z=z,e[m].st=i,mp[make_pair(x,y)]=m;
if(tp==2)e[mp[make_pair(x,y)]].ed=i,mp.erase(make_pair(x,y));
if(tp==3)p[i]=make_pair(x,y);
}
for(int i=1;i<=m;i++)if(!e[i].ed)e[i].ed=q+1;
// for(int i=1;i<=m;i++)printf("(%d,%d,%d):[%d,%d]\n",e[i].x,e[i].y,e[i].z,e[i].st,e[i].ed);
for(int i=1,j=1;i<=q;i++){
while(j<=m&&e[j].st<=i)LINK(j++);
if(p[i]!=make_pair(0,0))printf("%d\n",ask(i,split(p[i].first,p[i].second)));
}
return 0;
}
V.CF1299D Around the World
手画几个不存在长度大于 \(3\) 的经过点 \(1\) 的简单环的图，就会发现，这张图必定满足如下两个性质：
- 点 \(1\) 是个典型的割点，因为不存在过长的简单环。
- 在上述基础下，考虑 \(1\) 的邻边，就会发现要么该邻边是桥（这样显然不会出现包含 \(1\) 的大环），要么 \(1\)、该邻边的端点、另一条邻边的端点成三元环（显然这仍然符合要求），且上述两个端点要么没有其余连边，要么本身就是割点（即，其连接三元环与另外一大坨分量，且该分量中没有连到 \(1\) 的其余邻边方向的边）。
于是我们便考虑，依次遍历每条邻边（假如是上述三元环情形，则三元环的两条邻边可以一起判断，具体下文再说），判断该邻边是否保留。这似乎是个类似于背包的东西。
但是，因为这题要求不存在异或和为 \(0\) 的非简单环，所以就要满足两点：
- 保留的分量内部不能自己就出现了上述环；
- 保留的分量中的环不能与其它分量中的环发生
化学反应出现上述环。
这似乎意味着我们背包的维数要是一个线性基，然后要支持合并当前线性基的状态与一条邻边的线性基状态？这可能吗？
于是，抱着试一试的思想，看到了数据范围：\(<32\)。
What？\(32\)？那不就显然可以了吗？\(5\) 位的线性基总共才有多少？
一个非常松的上界的估计是 \(32^5=2^{25}\)，三千万出头，但已经让人跃跃欲试想要爆搜了；一个稍微紧一点的上界估计是，\(d_0\) 因为最高位是 \(0\)，所以有 \(2^{0+1}=2\) 种可能；同理，\(d_1\) 有 \(2^{1+1}=4\) 种可能，\(d_2\) 就有 \(2^{2+1}=8\) 种……因此总共是 \(2\times4\times8\times16\times32=32768\) 种，好像已经没问题了！
我们再排除掉那些不合法的线性基（其中存在一组异或和为 \(0\) 的子集）以及等价的线性基（这个可以通过1.3.求第\(k\)小异或和中介绍的构建 \(d_x\) 最小的线性基的方法来判定两组线性基是否等价，因为等价的线性基所对应的最小线性基是相同的）。爆搜发现总计 \(374\) 种。
\(374\) 就可以平方地预处理两个线性基合并的结果，然后在背包的时候直接用即可。
现在我们考虑如何背包。显然，初始线性基是全零线性基。接着，每遍历一条邻边，就有如下可能：
- 邻边所对应的分量中存在不合法的环。这时这条边默认断掉，可以跳过。
- 邻边是桥。于是枚举这条边断掉与否背包即可。
- 邻边连接三元环。此时，断掉三元环中某一条边仅仅会破坏三元环，只有全部断掉才会真正断开该分量。于是，我们有两种方法合并一个不包含三元环的线性基，一种方法合并一个包含三元环的线性基，一种方法啥也不合并。直接背包即可。
需要注意的是，在搜索构建分量的线性基时，有几个细节：
- 搜索到环的时候，观察发现环会被正反搜出两次，但是每次接口的两个点都是相同的。于是我们仅在一段点更小的那次将其插入线性基（具体哪端随便）。
- 假如搜索到线性基已经不合法了，千万不要急着退出。一定要搜完整个分量，不然可能会出现三元环的情形导致退早了该分量又从另一端进来一次。debug 一下午，惨痛的教训！
时间复杂度 \(374n\)。
代码：
#include<bits/stdc++.h>
using namespace std;
namespace Initialize{
int id[1<<20],all,r[500][500];
struct Linear_Basis{
int d[5];
int&operator[](const int&x){return d[x];}
bool ins(int x){
for(int i=4;i>=0;i--){
if(!(x&(1<<i)))continue;
if(!d[i]){d[i]=x;return true;}
x^=d[i];
}
return false;
}
void comp(){for(int i=0;i<5;i++)for(int j=i-1;j>=0;j--)if((d[i]^d[j])<d[i])d[i]^=d[j];}
int HASH()const{int ret=0;for(int i=0;i<5;i++)ret<<=(i+1),ret+=d[i];return ret;}
int Hash(){comp();return id[HASH()];}
friend int operator+(Linear_Basis&u,Linear_Basis&v){
Linear_Basis w=u;
for(int i=0;i<5;i++)if(v[i]&&!w.ins(v[i]))return -1;
return w.Hash();
}
void print()const{for(int i=0;i<5;i++)printf("%d ",d[i]);puts("");}
void clear(){for(int i=0;i<5;i++)d[i]=0;}
}lb;
vector<Linear_Basis>v;
void dfs(int pos){
if(pos==5){lb.comp();if(id[lb.HASH()]==-1)id[lb.HASH()]=all++,v.push_back(lb);return;}
Linear_Basis tmp=lb;
for(int i=0;i<(1<<pos);i++)if(lb.ins(i+(1<<pos)))dfs(pos+1),lb=tmp;
dfs(pos+1),lb=tmp;
}
void init(){
memset(id,-1,sizeof(id)),dfs(0);
// printf("%d\n",all);for(auto i:v)printf("%d:",i.HASH()),i.print();
for(int i=0;i<all;i++)for(int j=0;j<all;j++)r[i][j]=v[i]+v[j];
}
}
using namespace Initialize;
int n,m;
namespace Graph{
const int mod=1e9+7;
int head[100100],cnt,dis[100100];
struct node{int to,next,val;}edge[200100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
bool vis[100100];
int sp;
bool dfs(int x,int fa){
vis[x]=true;
bool ret=true;
for(int i=head[x];i!=-1;i=edge[i].next)if(edge[i].to!=fa){
if(vis[edge[i].to]){
if(edge[i].to==1){sp=dis[x]^edge[i].val;continue;}
if(edge[i].to>x&&!lb.ins(dis[x]^dis[edge[i].to]^edge[i].val))ret=false;
continue;
}
dis[edge[i].to]=dis[x]^edge[i].val;
if(!dfs(edge[i].to,x))ret=false;
}
return ret;
}
int f[510],g[510],res;
void solve(){
vis[1]=true;
f[all-1]=1;
for(int i=head[1];i!=-1;i=edge[i].next){
if(vis[edge[i].to])continue;
sp=-1,lb.clear(),dis[edge[i].to]=edge[i].val;
if(!dfs(edge[i].to,1))continue;
// lb.print(),printf("%d\n",sp);
int x=lb.Hash();
memset(g,0,sizeof(g));
for(int j=0;j<all;j++)if(r[x][j]!=-1)(g[r[x][j]]+=(f[j]<<(sp!=-1))%mod)%=mod;
if(sp!=-1&&lb.ins(sp)){
x=lb.Hash();
for(int j=0;j<all;j++)if(r[x][j]!=-1)(g[r[x][j]]+=f[j])%=mod;
}
for(int j=0;j<all;j++)(f[j]+=g[j])%=mod;
}
for(int i=0;i<all;i++)(res+=f[i])%=mod;
printf("%d\n",res);
}
}
using namespace Graph;
int main(){
init(),scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),ae(x,y,z);
solve();
return 0;
}
Part5.线性基可形成的所有不同异或值的和
I.CF724G Xor-matic Number of the Graph
这题整整卡了我5个小时，心态崩溃。
首先，我们先来考虑一下，线性基中所有异或和的和是什么呢？
我们考虑按位处理。对于第\(i\)位，只有所有第\(i\)位为\(1\)的\(d_x\)才会影响这一位的取值。
设共有\(k\)个第\(i\)位为\(1\)的\(d_x\)，且一共有\(tot\)个非零的\(d_x\)。则那\(tot-k\)个第\(i\)位为\(0\)的\(d_x\)，无论选不选，都不会有影响，故共\(2^{tot-k}\)种方案。而那\(k\)个第\(i\)位为\(1\)的\(d_x\)，只有选择奇数个，最终才会留下一个\(1\)。
则所有最终异或和中第\(i\)位为\(1\)的方案数量为：
\(2^{tot-k}\times\sum\limits_{j\operatorname{mod}2\equiv1}C_k^j\)
我们又有\(\sum\limits_{j\operatorname{mod}2\equiv1}C_k^j=\begin{cases}0\ (k=0)\\2^{k-1}\ (k>0)\end{cases}\)
故\(2^{tot-k}\times\sum\limits_{j\operatorname{mod}2\equiv1}C_k^j=\begin{cases}0\ (k=0)\\2^{tot-1}\ (k>0)\end{cases}\)
于是我们发现只要存在一个\(d_x\)的第\(i\)位上为\(1\)，这位上就会有\(2^{tot-1}\)种方案（即半数方案）异或值为\(1\)。而如果不存在这样一个\(d_x\)，则这位上无论如何都是\(0\)。
因此我们只需要求出所有非零的\(d_x\) \(\operatorname{or}\)在一起的结果，这个结果的非\(0\)位有\(2^{tot-1}\)种方式做出贡献。因此总答案即为\((\bigvee\limits_{d_i\neq 0}d_i)\times 2^{tot-1}\)。
现在我们回到本题。很明显，同前几题一样，仍然可以搜出所有的环并丢入线性基中。但是这回，因为\((u,v)\)不是唯一的，这是否意味着我们要暴力每一组\((u,v)\)，然后到线性基中求值呢？
不需要。我们发现如果设节点\(i\)到某个指定节点的距离为\(dis_i\)的话，则\(u\)到\(v\)的距离实际上就是\(dis_u\operatorname{xor}dis_v\)。
因此我们实际上是从集合\(\{dis_i\}\)中选择任意两个值异或在一起并在线性基中求值。但是这回我们不是求线性基中所有东西的异或和了——而是求线性基中所有东西的（异或和再异或上\((dis_u\operatorname{xor}dis_v)\)）的和。
我们可以把该集合中所有数放在一起，一起按位求值。
我们设一个\(tmp=\bigvee\limits_{d_i\neq 0}d_i\)。则\(tmp\)的第\(i\)位如果为\(1\)，则它有一半的方案为\(0\)，一半的方案为\(1\)，因此会对集合\(\{dis_i\}\)中每一对数都能产生\(2^{tot-1}\)种方案。设此集合大小为\(sz\)，则共\(2^{tot-1}\times\dfrac{sz(sz-1)}{2}\)种方案。
而如果\(tmp\)的第\(i\)位为\(0\)的话，无论如何异或和的第\(i\)位都是\(0\)，因此只有在集合\(\{dis_i\}\)选取两个第\(i\)位不同的数拼一起最终结果才是\(1\)。设\(\{dis_i\}\)中共有\(cnt\)个数第\(i\)位是\(1\)，则共有\(2^{tot}\times cnt\times(sz-cnt)\)种方案。
最终的统计答案函数：
int calc(){
ll tmp=0;
int ret=0,sz=v.size();
for(int i=62;i>=0;i--)if(d[i])tmp|=d[i];
for(int i=62;i>=0;i--){
int cnt=0;
for(ll j:v)cnt+=((j>>i)&1);
if(tmp&(1ll<<i))(ret+=((1ll<<i)%mod)*((1ll<<(tot-1))%mod)%mod*((1ll*sz*(sz-1)/2)%mod)%mod)%=mod;
else(ret+=((1ll<<i)%mod)*((1ll<<tot)%mod)%mod*(1ll*cnt*(sz-cnt)%mod)%mod)%=mod;
}
return ret;
}
然后只要注意这张图可能不连通，要对于每个连通块分开讨论即可。
代码：
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int n,m,head[101000],cnt,res;
ll dis[101000];
vector<ll>v;
struct lb{//linear basis?
ll d[64];
int tot;
void print(){
for(int i=0;i<=62;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
void clear(){memset(d,0,sizeof(d)),tot=0;}
lb(){memset(d,0,sizeof(d)),tot=0;}
void operator +=(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x,tot++;break;}
}
}
ll& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=62;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=62;i>=0;i--)if(y[i])z+=y[i];
return z;
}
int calc(){//calculate the number of possible xor values, from the vector v
ll tmp=0;
int ret=0,sz=v.size();
for(int i=62;i>=0;i--)if(d[i])tmp|=d[i];
for(int i=62;i>=0;i--){
int cnt=0;
for(ll j:v)cnt+=((j>>i)&1);
if(tmp&(1ll<<i))(ret+=((1ll<<i)%mod)*((1ll<<(tot-1))%mod)%mod*((1ll*sz*(sz-1)/2)%mod)%mod)%=mod;
else(ret+=((1ll<<i)%mod)*((1ll<<tot)%mod)%mod*(1ll*cnt*(sz-cnt)%mod)%mod)%=mod;
}
return ret;
}
}LB;
struct node{
int to,next;
ll val;
}edge[400100];
void ae(int u,int v,ll w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
bool vis[100100];
void dfs(int x){
vis[x]=true,v.push_back(dis[x]);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!vis[edge[i].to])dis[edge[i].to]=dis[x]^edge[i].val,dfs(edge[i].to);
else LB+=dis[x]^dis[edge[i].to]^edge[i].val;
}
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(ll i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(x,y,z);
for(int i=1;i<=n;i++)if(!vis[i])dfs(i),(res+=LB.calc())%=mod,LB.clear(),v.clear();
printf("%d\n",res);
return 0;
}
II.【清华集训2014】玛里苟斯
当\(k=1\)的情况之前已经说过，总和是\((\bigvee\limits_{d_i\neq 0}d_i)\times 2^{tot-1}\)。如果我们设\(\bigvee\limits_{d_i\neq 0}d_i=tmp\)的话，则是\(tmp\times 2^{tot-1}\)。然后现在因为是求期望，因此除以\(2^{tot}\)即可。则最终结果为\(\dfrac{tmp}{2}\)。
因为答案在\(2^{64}\)以内，所以\(tmp\)直接用unsigned long long存一下，然后最后一位特判到底是无小数还是输出.5即可。
此部分代码：
void calc1(){
if(tmp&1)printf("%llu.5\n",tmp>>1);
else printf("%llu\n",tmp>>1);
}
当\(k=2\)时，我们设\(tmp\)的第\(i\)位为\(b_i\)。则每一位上都有\(\dfrac{2^{tot-1}}{2^{tot}}=1/2\)的概率出现一个\(1\)，则总和即为\(\sum\limits_{i=0}^{63}b_i\times2^{i}\times (1/2)\)。但是我们还要平个方，于是便得到了\((\sum\limits_{i=0}^{63}b_i\times2^{i-1})^2\)。
暴力拆开，我们要求的东西就是\(\sum\limits_{i=0}^{63}\sum\limits_{j=0}^{63}b_ib_j2^{i+j-2}\)。
则显然，只有\(b_i\)与\(b_j\)都为\(1\)的地方才能贡献出\(2^{i+j-2}\)。
但是这里又有一种情况，就是在所有\(a_i\)（即原数组）中，总有第\(i\)位同第\(j\)位相等。这就意味着第\(i\)位与第\(j\)位绑定了，它们总是相同。如果绑定了，这两者因为始终相等，概率就不是两个\(1/2\)乘在一起，而是直接一个\(1/2\)了！
我们设是否绑定为一个bool值\(sm\)来表示，如果为true就是绑定上了。则最终答案即为\(\sum\limits_{i=0}^{63}\sum\limits_{j=0}^{63}b_ib_j2^{i+j-2+sm}\)。
等等，那输出怎么办？它要求输出精确值呀！
没关系！当\(i+j\geq2\)时，结果肯定是整数；
当\(i+j=1\)时，末尾是\(0\)或\(0.5\)；
当\(i+j=0\)时，有且只有\(i=j=0\)才会出现这种情况，而此时因为\(i=j\)，所以肯定就绑定上了！因此它最终是\(b_0\times b_0\times2^{-1}\)，结尾仍是\(0\)或\(0.5\)。
所以最终结尾仍是\(0\)或\(0.5\)。
但是这又有问题了——它只保证结果小于\(2^{63}\)，但是没有保证中间结果小于\(2^{63}\)！
我们要么用double储存，要么用__int128，要么也可以用两个unsigned long long拼一起模拟__int128。
这里采取两个ull拼一起的方法。
此部分代码：
void calc2(){
for(int i=0;i<32;i++)for(int j=0;j<32;j++){
if(!(tmp&(1ull<<i)))continue;
if(!(tmp&(1ull<<j)))continue;
bool sm=true;
for(int p=1;p<=n;p++)if(((a[p]>>i)&1)!=((a[p]>>j)&1)){sm=false;break;}
if(i+j-2+sm<0)floa++;
else inte+=(1ull<<(i+j-2+sm));
}
inte+=(floa>>1),floa&=1;
if(floa)printf("%llu.5\n",inte);
else printf("%llu\n",inte);
}
当\(k\geq 3\)时，因为答案小于\(2^{63}\)，你开一个\(3\)次根，结果肯定小于\(2^{22}\)。所以直接暴力枚举\(2^{22}\)种线性基的子集即可通过。当然，这里仍得使用两个ull进行拼接。
此部分代码：
void calc3(){
for(int i=0;i<64;i++)if(d[i])arr[tot++]=i;
for(ll i=0;i<(1llu<<tot);i++){
ll s=0;
for(int j=0;j<tot;j++)if(i&(1llu<<j))s^=d[arr[j]];
ll p=0,q=1;
for(int l=0;l<k;l++)p*=s,q*=s,p+=(q>>tot),q&=(1llu<<tot)-1;
inte+=p,floa+=q;
inte+=(floa>>tot),floa&=(1llu<<tot)-1;
}
if(floa)printf("%llu.5\n",inte);
else printf("%llu\n",inte);
}
Part6.线性基区间修改
有的时候，我们会遇到这样的题，要你支持两种操作：
- 区间异或上某数
- 求区间上线性基的某种应用（即上文中介绍的线性基的诸多用法之一）
这时应该如何处理呢？
I.[Ynoi2013]无力回天NOI2017
这里就是例子之一，区间异或+区间最大异或和。
考虑到线性基只具有可加性，并不具有可修改性；故我们不能直接上线段树套线性基。
我们考虑对序列作差分——考虑令一个\(b_i=a_i\operatorname{xor}a_{i+1}\)。此时，区间修改在差分数组上就只需要修改一头一尾的值。
而如果要求区间的线性基的话，我们只需要求出差分数组的线性基，然后再加入区间末尾的一个数即可。可以发现此种线性基就等价于原本的线性基（因为线性基是异或等价的）。
于是我们只需要使用两棵线段树，一棵维护差分数组的线性基，复杂度\(O(n\log^3n)\)；一棵维护原序列的元素（因为我们最终是要加入区间末尾的那个数的），复杂度\(O(n\log n)\)。
代码：
#include<bits/stdc++.h>
using namespace std;
int n,m,a[50100];
struct lb{//linear basis?
int d[32];
void print(){
for(int i=0;i<=29;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(int x){
for(int i=29;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
int& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=29;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb x,lb y){
lb z=x;
for(int i=29;i>=0;i--)if(y[i])z+=y[i];
return z;
}
int num(){for(int i=29;i>=0;i--)if(d[i])return d[i];return 0;}
int calc(int ip=0){
for(int i=29;i>=0;i--)if((ip^d[i])>ip)ip^=d[i];
return ip;
}
};
#define lson x<<1
#define rson x<<1|1
#define mid ((l+r)>>1)
namespace AES{//adjecent elements' segtree
lb seg[200100];
void build(int x,int l,int r){
if(r-l==1){seg[x]+=a[l]^a[r];return;}
build(lson,l,mid),build(rson,mid,r),seg[x]=seg[lson]+seg[rson];
}
void modify(int x,int l,int r,int P,int val){
if(l>P||r<=P)return;
if(r-l==1){val^=seg[x].num();seg[x]=lb();seg[x]+=val;return;}
modify(lson,l,mid,P,val),modify(rson,mid,r,P,val),seg[x]=seg[lson]+seg[rson];
}
lb query(int x,int l,int r,int L,int R){
if(L<=l&&r<=R)return seg[x];
if(mid>=R)return query(lson,l,mid,L,R);
if(mid<=L)return query(rson,mid,r,L,R);
return query(lson,l,mid,L,R)+query(rson,mid,r,L,R);
}
}
namespace OSS{//original sequence's segtree
int seg[200100];
void pushdown(int x){seg[lson]^=seg[x],seg[rson]^=seg[x],seg[x]=0;}
void build(int x,int l,int r){
if(l==r){seg[x]=a[l];return;}
build(lson,l,mid),build(rson,mid+1,r);
}
void modify(int x,int l,int r,int L,int R,int val){
if(l>R||r<L)return;
if(L<=l&&r<=R){seg[x]^=val;return;}
pushdown(x),modify(lson,l,mid,L,R,val),modify(rson,mid+1,r,L,R,val);
}
int query(int x,int l,int r,int P){
if(l==r)return seg[x];
pushdown(x);
return P<=mid?query(lson,l,mid,P):query(rson,mid+1,r,P);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
if(n!=1)AES::build(1,1,n);OSS::build(1,1,n);
for(int i=1,a,b,c,d;i<=m;i++){
scanf("%d",&a),scanf("%d%d%d",&b,&c,&d);
if(a==1){
OSS::modify(1,1,n,b,c,d);
AES::modify(1,1,n,b-1,d);
AES::modify(1,1,n,c,d);
}else{
lb res;
if(b!=c)res=AES::query(1,1,n,b,c);
res+=OSS::query(1,1,n,c);
printf("%d\n",res.calc(d));
}
}
return 0;
}
II.CF587E Duff as a Queen
和上题几乎一致，可以被看作是双倍经验，代码就不贴了。
INF.总结
线性基是一种很奇妙的东西，在求关于异或的东西的时候非常实用。同时，要注意它要与其它一些可以使用异或的数据结构区分，如01trie等。
它主要的用途有：
- 最大/最小/\(k\)大异或和
- 异或和数量
- 异或和的和
同时又可以找到“子集”“子序列”等字眼，或者是图论中的某条路径的异或和时，就可以往线性基方向想了。
希望我的讲解能带你们听懂线性基。
参考材料：
