[USACO20OPEN]Sprinklers 2: Return of the Alfalfa P
LXV.[USACO20OPEN]Sprinklers 2: Return of the Alfalfa P
首先，一个合法的方案，肯定是有一条从左到右向下延伸的轮廓线：
例如：
其中，蓝色系格子是玉米，红色系格子是苜蓿；浅蓝色位置必须放玉米喷射器，深红色格子必须放苜蓿喷射器。深蓝和浅红格子放不放均可。更一般地说，所有的转角处，都是必须放喷射器的位置。
因此我们可以考虑DP：
假设一定至少放了一个玉米喷射器（有可能有没有任何玉米喷射器的情况，但当且仅当左下角可以放喷射器时，这时只要在左下角放一个苜蓿，其他位置就可以随便放或不放喷射器了），则设\(f[i][j]\)表示在位置\((i,j)\)放了一个玉米时的方案数。
我们思考一下，当位置\((i,j)\)已经被放入玉米后，有哪些位置的发射器种类以及决定了：
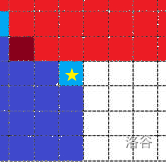
如图，五角星格子就是\((i,j)\)，
那么\((i,j)\)左下角的深蓝色格子肯定已经被决定了；
第\((i-1)\)行上，肯定有一个深红格子存在（不然\((i-1)\)行就没有颜色了），因此实际上，只有以\((i,j+1)\)为左上角的矩形，里面的颜色尚未决定。
因此我们设一个前缀和\(s_{i,j}\)，表示以\((i,j)\)为左上角的矩形里面有多少个位置没有牛。
先考虑初始化。
- 位置\((i,j)\)中\(i\neq 1\)，即不位于第\(1\)行。
如图，则位置\((i-1,1)\)必有一个苜蓿。显然，只有位置\((i-1,1)\)不是牛，该位置才可以作为起始点。
则\(f[i][j]=2^{s_{1,1}-s_{i,j+1}-2}\)。
- 有\(i=1\)。
位置\((i-1,1)\)的那个苜蓿不需要放，直接有
\(f[i][j]=2^{s_{1,1}-s_{i,j+1}-1}\)。
考虑转移。
我们枚举一个\((k,l)\)，且\(k<i,l<j\)。
则位置\((i-1,l+1)\)肯定有个苜蓿。如果位置\((i-1,l+1)\)没有牛，则可以转移。
如图，黄星要想从紫星转移来，那么深红位置是必须放置苜蓿的。
则有\(f[i][j]=\sum\limits_{k=1}^{i-1}\sum\limits_{l=1}^{j-1}f[k][l]*2^{s_{k,l+1}-s_{i,j+1}-2}*[(i-1,l+1)\text{没有牛}]\)
代码：
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int n,s[2010][2010],f[2020][2020],bin[4001000],res;
char g[2010][2010];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%s",g[i]+1);
for(int i=n;i;i--)for(int j=n;j;j--)s[i][j]=s[i+1][j]+s[i][j+1]-s[i+1][j+1]+(g[i][j]=='.');
bin[0]=1;
for(int i=1;i<=s[1][1];i++)bin[i]=(bin[i-1]<<1)%mod;
// for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",s[i][j]);puts("");}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
if(g[i][j]=='W')continue;
if(g[i-1][1]=='.')f[i][j]=bin[s[1][1]-s[i][j+1]-2];
if(i==1)f[i][j]=bin[s[1][1]-s[i][j+1]-1];
for(int k=1;k<i;k++)for(int l=1;l<j;l++){
if(g[k][l]=='W'||g[i-1][l+1]=='W')continue;
(f[i][j]+=1ll*bin[s[k][l+1]-s[i][j+1]-2]*f[k][l]%mod)%=mod;
}
if(g[n][j+1]=='.')(res+=1ll*f[i][j]*bin[s[i][j+1]-1]%mod)%=mod;
if(j==n)(res+=f[i][j])%=mod;
}
// for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",f[i][j]);puts("");}
if(g[n][1]=='.')(res+=bin[s[1][1]-1])%=mod;
printf("%d\n",res);
return 0;
}
很明显这种东西是\(O(n^4)\)的，期望得分\(24\%\)。考虑优化。
初始化过程是\(O(n^2)\)的，没问题。关键是转移的地方。
我们搬出式子：
\(f[i][j]=\sum\limits_{k=1}^{i-1}\sum\limits_{l=1}^{j-1}f[k][l]*2^{s_{k,l+1}-s_{i,j+1}-2}*[(i-1,l+1)\text{没有牛}]\)
先把这个东西拆成和\((i,j)\)有关的和\((k,l)\)有关的部分：
\(f[i][j]=\sum\limits_{k=1}^{i-1}\sum\limits_{l=1}^{j-1}\dfrac{f[k][l]*2^{s_{k,l+1}}*[(i-1,l+1)\text{没有牛}]}{2^{s_{i,j+1}+2}}\)
再调整求和顺序：
\(f[i][j]=\dfrac{\sum\limits_{l=1}^{j-1}[(i-1,l+1)\text{没有牛}]*\sum\limits_{k=1}^{i-1}f[k][l]*2^{s_{k,l+1}}}{2^{s_{i,j+1}+2}}\)
然后设一个前缀和\(sum1[i][j]=\sum\limits_{k=1}^{i}f[k][j]*2^{s_{k,j+1}}\)
往里面一代：
\(f[i][j]=\dfrac{\sum\limits_{l=1}^{j-1}[(i-1,l+1)\text{没有牛}]*sum1[i-1][l]}{2^{s_{i,j+1}+2}}\)
这样复杂度就被优化成了\(O(n^3)\)，期望得分\(54\%\)。
代码：
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
const int inv2=5e8+4;
int n,s[2010][2010],f[2020][2020],bin[4001000],inv[4001000],res,sum[2020][2020];
char g[2010][2010];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%s",g[i]+1);
for(int i=n;i;i--)for(int j=n;j;j--)s[i][j]=s[i+1][j]+s[i][j+1]-s[i+1][j+1]+(g[i][j]=='.');
bin[0]=inv[0]=1;
for(int i=1;i<=s[1][1];i++)bin[i]=(bin[i-1]<<1)%mod,inv[i]=(1ll*inv[i-1]*inv2)%mod;
// for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",s[i][j]);puts("");}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
if(g[i][j]!='W'){
if(g[i-1][1]=='.')f[i][j]=bin[s[1][1]-s[i][j+1]-2];
if(i==1)f[i][j]=bin[s[1][1]-s[i][j+1]-1];
for(int k=1;k<j;k++){
if(g[i-1][k+1]=='W')continue;
(f[i][j]+=1ll*sum[i-1][k]*inv[s[i][j+1]+2]%mod)%=mod;
}
if(g[n][j+1]=='.')(res+=1ll*f[i][j]*bin[s[i][j+1]-1]%mod)%=mod;
if(j==n)(res+=f[i][j])%=mod;
}
sum[i][j]=(1ll*f[i][j]*bin[s[i][j+1]]+sum[i-1][j])%mod;
}
// for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",f[i][j]);puts("");}
if(g[n][1]=='.')(res+=bin[s[1][1]-1])%=mod;
printf("%d\n",res);
return 0;
}
继续尝试优化。
\(f[i][j]=\dfrac{\sum\limits_{l=1}^{j-1}[(i-1,l+1)\text{没有牛}]*sum1[i-1][l]}{2^{s_{i,j+1}+2}}\)
发现我们现在就可以设一个\(sum2[i][j]=\sum\limits_{l=1}^j[(i,l+1)\text{没有牛}]*sum1[i][l]\)
则直接有\(f[i][j]=\dfrac{sum2[i-1][j-1]}{2^{s_{i,j+1}+2}}\)
复杂度\(O(n^2)\)，期望得分\(100\%\)。
代码：
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
const int inv2=5e8+4;
int n,s[2010][2010],f[2020][2020],bin[4001000],inv[4001000],res,sum1[2020][2020],sum2[2020][2020];
char g[2010][2010];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%s",g[i]+1);
for(int i=n;i;i--)for(int j=n;j;j--)s[i][j]=s[i+1][j]+s[i][j+1]-s[i+1][j+1]+(g[i][j]=='.');
bin[0]=inv[0]=1;
for(int i=1;i<=s[1][1];i++)bin[i]=(bin[i-1]<<1)%mod,inv[i]=(1ll*inv[i-1]*inv2)%mod;
// for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",s[i][j]);puts("");}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
if(g[i][j]!='W'){
if(g[i-1][1]=='.')f[i][j]=bin[s[1][1]-s[i][j+1]-2];
if(i==1)f[i][j]=bin[s[1][1]-s[i][j+1]-1];
(f[i][j]+=1ll*sum2[i-1][j-1]*inv[s[i][j+1]+2]%mod)%=mod;
if(g[n][j+1]=='.')(res+=1ll*f[i][j]*bin[s[i][j+1]-1]%mod)%=mod;
if(j==n)(res+=f[i][j])%=mod;
}
sum1[i][j]=(1ll*f[i][j]*bin[s[i][j+1]]+sum1[i-1][j])%mod;
sum2[i][j]=(sum2[i][j-1]+(g[i][j+1]=='W'?0:sum1[i][j]))%mod;
}
// for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",f[i][j]);puts("");}
if(g[n][1]=='.')(res+=bin[s[1][1]-1])%=mod;
printf("%d\n",res);
return 0;
}
