CF954I Yet Another String Matching Problem

VII.CF954I Yet Another String Matching Problem

FFT做字符串匹配就是有意思

我们首先必须要搞清楚暴力匹配是什么样的过程。

例：

位置	0	1	2	3
\(t\)的子串	a	b	a	c
\(s\)	b	c	a	b

则我们共得到四对需要修改的对：\((a-b)(b-c)(a-a)(c-b)\)

画出图来就是这个：

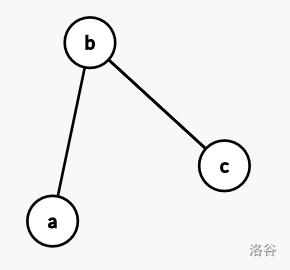
如果想一想就可以发现，我们在每一块连通块中求出一棵生成树，则生成树的边数就是处理完这个连通块所需要的次数。显然，该次数为（连通块大小-1）。

我们可以采用冰茶姬。对于每一条新边，在冰茶姬中连边，如果连边成功，答案加1；否则，即两个点已经在同一个连通块中，忽略不计。

如何求出对于\(t\)的每个子串，它与\(s\)间到底连了哪些边呢？我们采用FFT。

\(6^2\)枚举这条边的两个端点（例如\((a,b)\)或\((b,a)\)或\((a,f)\)），然后直接FFT一卷完事，同我们前几道题的方法完全一致。

代码：

#include<bits/stdc++.h>
using namespace std;
const double pi=acos(-1);
int lim=1,lg,rev[1<<20],dsu[125010][6],ans[125010],S,T;
char s[125010],t[125010];
int ask(int x,int y){
	return dsu[x][y]==y?y:dsu[x][y]=ask(x,dsu[x][y]);
}
bool merge(int x,int y,int z){
	y=ask(x,y),z=ask(x,z);
	if(y==z)return false;
	dsu[x][y]=dsu[x][z];
	return true;
}
struct cp{
	double x,y;
	cp(double u=0,double v=0){x=u,y=v;}
	friend cp operator +(const cp &u,const cp &v){return cp(u.x+v.x,u.y+v.y);}
	friend cp operator -(const cp &u,const cp &v){return cp(u.x-v.x,u.y-v.y);}
	friend cp operator *(const cp &u,const cp &v){return cp(u.x*v.x-u.y*v.y,u.x*v.y+u.y*v.x);}
}f[1<<20],g[1<<20];
void FFT(cp *a,int tp){
	for(int i=0;i<lim;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
	for(int md=1;md<lim;md<<=1){
		cp rt=cp(cos(pi/md),tp*sin(pi/md));
		for(int stp=md<<1,pos=0;pos<lim;pos+=stp){
			cp w=cp(1,0);
			for(int i=0;i<md;i++,w=w*rt){
				cp x=a[pos+i],y=w*a[pos+md+i];
				a[pos+i]=x+y;
				a[pos+md+i]=x-y;
			}
		}
	}
}
void match(int x,int y){
	for(int i=0;i<lim;i++)f[i]=g[i]=cp(0,0);
	for(int i=0;i<S;i++)f[i]=cp(s[i]-'a'==x,0);
	for(int i=0;i<T;i++)g[i]=cp(t[i]-'a'==y,0);
	FFT(f,1),FFT(g,1);
	for(int i=0;i<lim;i++)f[i]=f[i]*g[i];
	FFT(f,-1);
	for(int i=S-1;i<T;i++)if((int)(f[i].x/lim+0.5)>=1)ans[i]+=merge(i,x,y);
}
int main(){
	scanf("%s%s",t,s),T=strlen(t),S=strlen(s),reverse(s,s+S);
	while(lim<=(S+T))lim<<=1,lg++;
	for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
	for(int i=S-1;i<T;i++)for(int j=0;j<6;j++)dsu[i][j]=j;
	for(int i=0;i<6;i++)for(int j=0;j<6;j++)match(i,j);
	for(int i=S-1;i<T;i++)printf("%d ",ans[i]);
	return 0;
}