数据结构之二叉 排序树
1)二叉顺序树查找操作:(注释内容来自《大话数据结构》)



2)二叉顺序树插入操作:



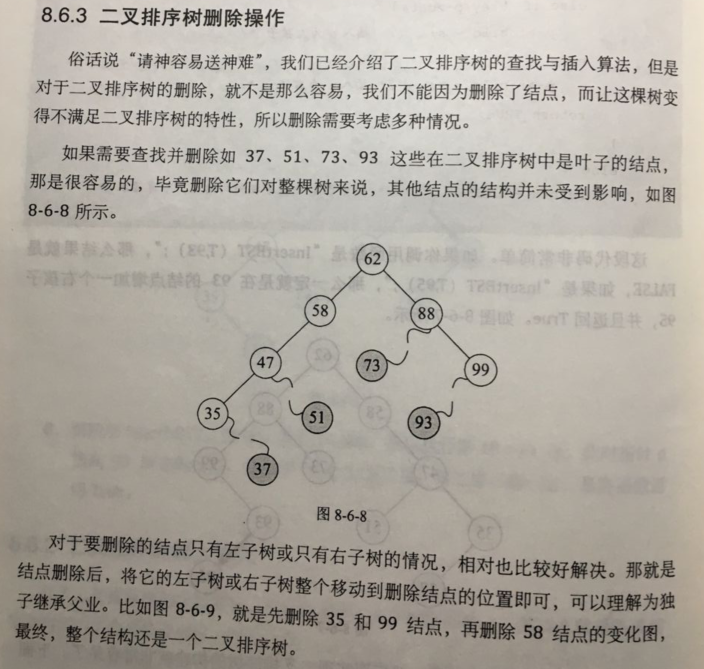
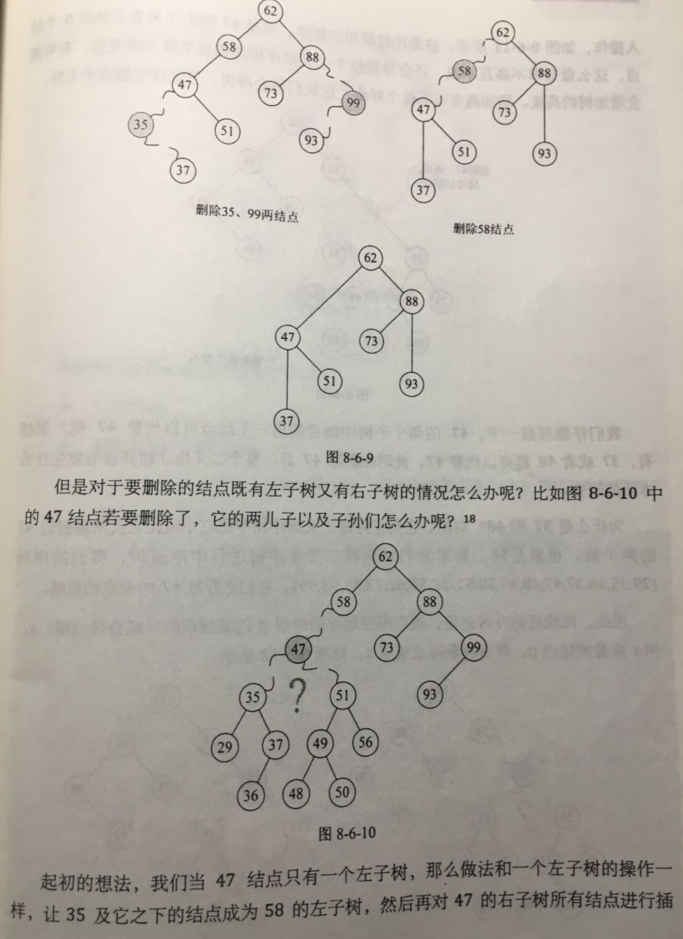
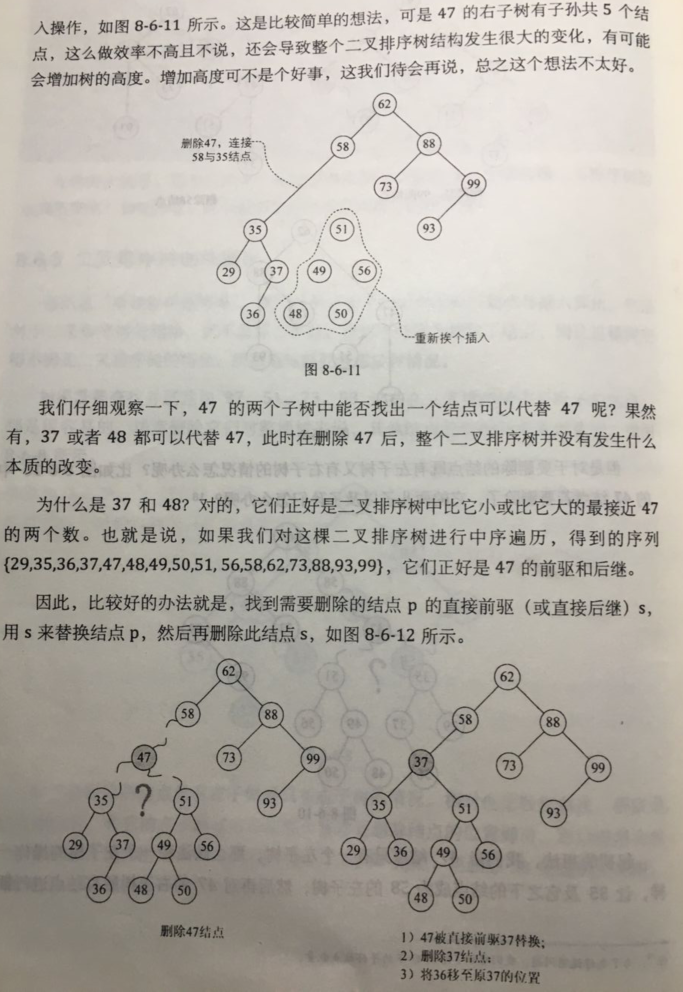
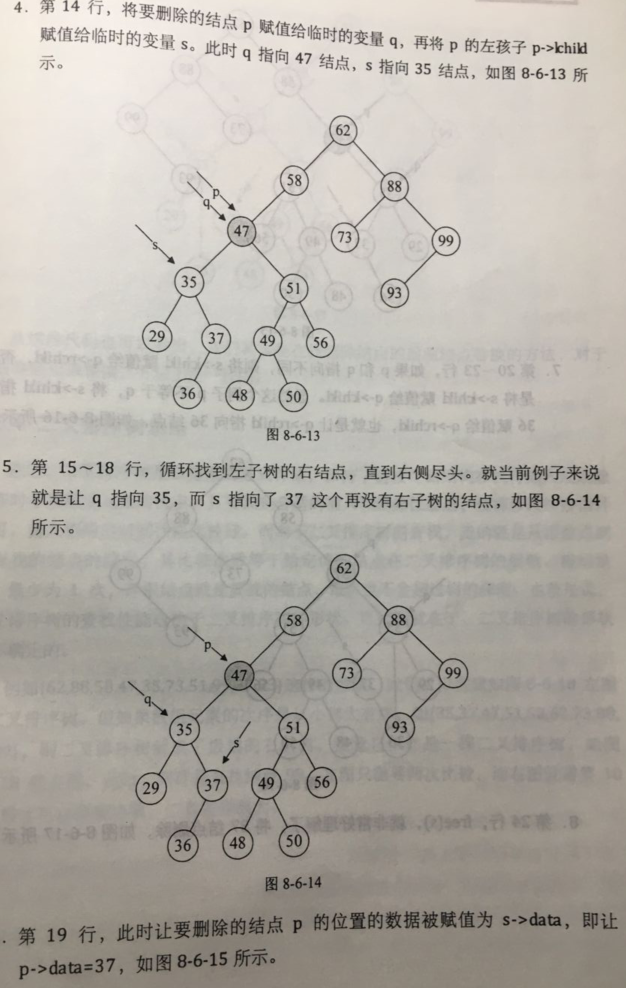
3)二叉顺序树删除操作:



完整代码如下:
1 #include "stdafx.h" 2 #include<iostream> 3 using namespace std; 4 typedef int Status; 5 #define FALSE 0 6 #define TRUE 1 7 typedef struct BiTNode 8 { 9 int data;//结点数据 10 struct BiTNode *lchild, *rchild; //左右孩子指针 11 }BiTNode,*BiTree; 12 13 //递归查找二叉排序树T中是否存在key, 14 //指针f指向T的双亲,其初始调用值为NULL 15 //若查找成功,则指针p指向该数据元素结点,并返回TRUE 16 //否则指针p指向查找路径上访问的最后一个结点并返回FALSE 17 Status SearchBST(BiTree T, int key, BiTree f, BiTree *p) 18 { 19 if (!T) //查找失败 20 { 21 *p = f; 22 return FALSE; 23 } 24 else if (key == T->data) //查找成功 25 { 26 *p = T; 27 return TRUE; 28 } 29 else if (key < T->data) 30 return SearchBST(T->lchild, key, T, p);//在左子树中继续查找 31 else 32 return SearchBST(T->rchild, key, T, p);//在右子树中继续查找 33 } 34 35 Status InsertBST(BiTree *T, int key) 36 { 37 BiTree p, s; 38 if (!SearchBST(*T, key, NULL, &p))//查找失败 39 { 40 s = new BiTNode; 41 s->data = key; 42 s->lchild = s->rchild = NULL; 43 if (!p) 44 *T = s; //插入s为新的根节点 45 else if (key < p->data) 46 p->lchild = s; //插入s为左孩子 47 else 48 p->rchild = s; //插入s为右孩子 49 } 50 else 51 return FALSE; // 树中已有关键字相同的结点,不再插入 52 } 53 54 //从二叉排序树中删除结点p,并重接它的左或右子树 55 Status Delete(BiTree *p) 56 { 57 BiTree q, s; 58 if ((*p)->rchild == NULL) //右子树空则只需重接它的左子树(待删结点是叶子也走此分支) 59 { 60 q = *p; 61 *p = (*p)->lchild; 62 free(q); 63 } 64 else if ((*p)->lchild == NULL) //只需重接它的右子树 65 { 66 q = *p; 67 *p = (*p)->rchild; 68 free(q); 69 } 70 else //左右子树均不空 71 { 72 q = *p; 73 s = (*p)->lchild; 74 while (s->rchild) //转左,然后向右到尽头(找待删结点的前驱) 75 { 76 q = s; 77 s = s->rchild; 78 } 79 (*p)->data = s->data; //s指向被删结点的直接前驱(将被删结点前驱的值取代被删结点的值) 80 if (q != *p) 81 q->rchild = s->lchild;//重接q的右子树 82 else 83 q->lchild = s->lchild;//重接q的左子树 84 free(s); 85 } 86 return TRUE; 87 } 88 89 //若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据元素结点, 90 //并返回TRUE;否则返回FALSE 91 Status DeleteBST(BiTree *T, int key) 92 { 93 if (!*T) //不存在关键字等于key的数据元素 94 return FALSE; 95 else 96 { 97 if (key == (*T)->data) //找到关键字等于key的数据元素 98 return Delete(T); 99 else if (key<(*T)->data) 100 return DeleteBST(&(*T)->lchild, key); 101 else 102 return DeleteBST(&(*T)->rchild, key); 103 } 104 } 105 106 107 int main() 108 { 109 int i; 110 int a[10] = { 62,88,58,47,35,73,51,99,37,93 }; 111 BiTree T = NULL; 112 113 for (i = 0; i<10; i++) 114 { 115 InsertBST(&T, a[i]); 116 } 117 DeleteBST(&T, 93); 118 DeleteBST(&T, 47); 119 cout<<"本样例建议断点跟踪查看二叉排序树结构"; 120 return 0; 121 }


