数据结构之[关键路径]以及[拓扑算法优化]
【1】关键路径(说明部分参考于:https://www.cnblogs.com/Braveliu/p/3461649.html)
在我的经验意识深处,“关键”二字一般都是指临界点。
凡事万物都遵循一个度的问题,那么存在度就会自然有临界点。
关键路径也正是研究这个临界点的问题。
在学习关键路径前,先了解一个AOV网和AOE网的概念:

用顶点表示活动,用弧表示活动间的优先关系的有向图:
称为顶点表示活动的网(Activity On Vertex Network),简称为AOV网。
与AOV网对应的是AOE(Activity On Edge)网即边表示活动的网。
AOE网是一个带权的有向无环图。
网中只有一个入度为零的点(称为源点)和一个出度为零的点(称为汇点)。
其中,顶点表示事件(Event),弧表示活动,权表示活动持续的时间。
通常,AOE网可用来估算工程的完成时间。
假如汽车生产工厂要制造一辆汽车,制造过程的大概事件和活动时间如上图AOE网:
我们把路径上各个活动所持续的时间之和称为路径长度,从源点到汇点具有最大长度的路径叫关键路径,在关键路径上的活动叫关键活动。
那么,显然对上图AOE网而言,所谓关键路径:
开始-->发动机完成-->部件集中到位-->组装完成。路径长度为5.5。
如果我们试图缩短整个工期,去改进轮子的生产效率,哪怕改动0.1也是无益的。
只有缩短关键路径上的关键活动时间才可以减少整个工期的长度。
例如如果制造发动机缩短为2.5天,整车组装缩短为1.5天,那么关键路径为4.5。
工期也就整整缩短了一天时间。
好吧! 那么研究这个关键路径意义何在?
假定上图AOE网中弧的权值单位为小时,而且我们已经知道黑深色的那一条为关键路径。
假定现在上午一点,对于外壳完成事件而言,为了不影响工期:
外壳完成活动最早也就是一点开始动工,最晚在两点必须要开始动工。
最大权值3表示所有活动必须在三小时之后完成,而外壳完成只需要2个小时。
所以,这个中间的空闲时间有一个小时,为了不影响整个工期,它必须最迟两点动工。
那么才可以保证3点时与发动机完成活动同时竣工,为后续的活动做好准备。
对AOE网有待研究的问题是:
(1)完成整个工程至少需要多少时间?
(2)那些活动是影响工程进度的关键?
今天研究是实例如下图所示:
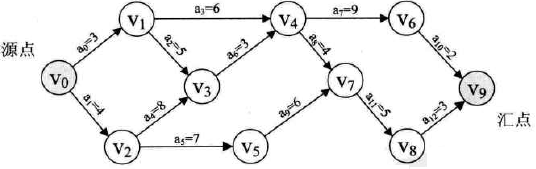
假想是一个有11项活动的AOE网,其中有9个事件(V1,V2,V3...V9)。
每个事件表示在它之前的活动已经完成,在它之后的活动可以开始。
如V1表示整个工程开始,V9表示整个共结束,V5表示a4和a5已经完成,a7和a8可以开始。
【2】关键路径算法:
(1)事件的最早发生时间etv(earliest time of vertex): 即顶点Vk的最早发生时间。
(2)事件的最晚发生时间ltv(latest time of vertex): 即顶点Vk的最晚发生时间。
也就是每个顶点对应的事件最晚需要开始的时间,超出此时间将会延误整个工期。
(3)活动的最早开工时间ete(earliest time of edge): 即弧ak的最早发生时间。
(4)活动的最晚开工时间lte(latest time of edge): 即弧ak的最晚发生时间,也就是不推迟工期的最晚开工时间。
然后根据最早开工时间ete[k]和最晚开工时间lte[k]相等判断ak是否是关键路径。
将AOE网转化为邻接表结构如下图所示:

与拓扑序列邻接表结构不同的地方在于,弧链表增加了weight域,用来存储弧的权值。
求事件的最早发生时间etv的过程,就是从头至尾找拓扑序列的过程。
因此,在求关键路径之前,先要调用一次拓扑序列算法的代码来计算etv和拓扑序列表。
数组etv存储事件最早发生时间
数组ltv存储事件最迟发生时间
全局栈用来保存拓扑序列

注意代码中的粗部分与原拓扑序列的算法区别。
第11-15行 初始化全局变量etv数组。
第21行 就是讲要输出的拓扑序列压入全局栈。
第 27-28 行很关键,它是求etv数组的每一个元素的值。
比如:假如我们已经求得顶点V0的对应etv[0]=0;顶点V1对应etv[1]=3;顶点V2对应etv[2]=4
现在我们需要求顶点V3对应的etv[3],其实就是求etv[1]+len<V1,V3>与etv[2]+len<V2,V3>的较大值
显然3+5<4+8,得到etv[3]=12,在代码中e->weight就是当前弧的长度。
如图所示:
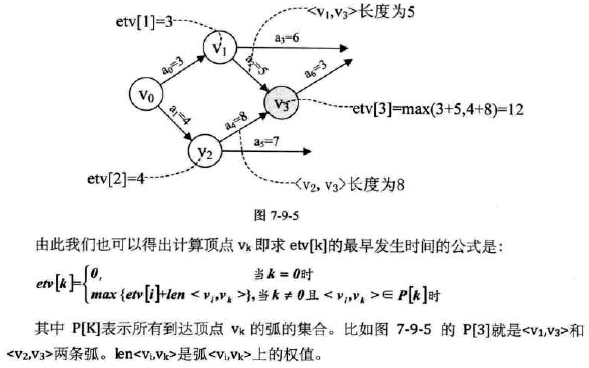
由此也可以得到计算顶点Vk即求etv[k]的最早发生时间公式如上。
下面具体分析关键路径算法:

1. 程序开始执行。第5行,声明了etv和lte两个活动最早最晚发生时间变量
2. 第6行,调用求拓扑序列的函数。
执行完毕后,全局数组etv和栈的值如下所示796,也就是说已经确定每个事件的最早发生时间。
3. 第7-9行初始化数组ltv,因为etv[9]=27,所以数组当前每项均为27。
4. 第10-19行为计算ltv的循环。第12行,先将全局栈的栈头出栈,由后进先出得到gettop=9。
但是,根据邻接表中信息,V9没有弧。所以至此退出循环。
5. 再次来到第12行,gettop=8,在第13-18行的循环中,V8的弧表只有一条<V8,V9>
第15行得到k=9,因为ltv[9]-3<ltv[8],所以ltv[8]=ltv[9]-3=24,过程如下图所示:

6. 再次循环,当gettop=7,5,6时,同理可计算出ltv相对应的值为19,25,13。
此时ltv值为:{27,27,27,27,27,13,25,19,24,27}
7. 当gettop=4时,由邻接表信息可得到V4有两条弧<V4,V6>和<V4,V7>。
通过第13-18行的循环,可以得到ltv[4]=min(ltv[7]-4,ltv[6]-9)=min(19-4,25-9)=15
过程分析如下图所示:

当程序执行到第20行时,相关变量的值如下图所示。
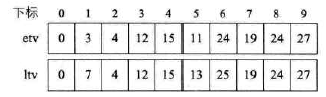
比如etv[1]=3而ltv[1]=7表示(如果单位按天计的话):
哪怕V1这个事件在第7天才开始也是可以保证整个工程按期完成。
你也可以提前V1时间开始,但是最早也只能在第3天开始。
8. 第20-31行是求另两个变量活动最早开始时间ete和活动最晚时间lte。
当 j=0 时,从V0顶点开始,有<V0,V2>和<V0,V1>两条弧。
当 k=2 时,ete=etv[j]=etv[0]=0
lte=ltv[k]-e->weight=ltv[2]-len<v0,v2>=4-4=0 此时ete == lte
表示弧<v0,v2>是关键活动,因此打印。
当 k=1 时,ete=etv[j]=etv[0]=0
lte=ltv[k]-e->weight=ltv[2]-len<v0,v1>=7-3=4 此时ete != lte
表示弧<v0,v1>并不是关键活动。如图所示:
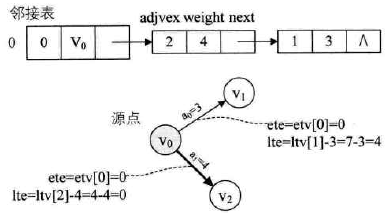
说明:ete表示活动<Vk,Vj>的最早开工时间,是针对弧来说的。
但是只有此弧的弧尾顶点Vk的事件发生了,它才可以开始,ete=etv[k]。
lte表示的是活动<Vk,Vj>最晚开工时间,但此活动再晚也不能等V1事件发生才开始。
而必须要在V1事件之前发生,所以lte=ltv[j]-len<Vk,Vj>。
9. j=1 直到 j=9 为止,做法完全相同。
最终关键路径如下图所示:

注意:本例是唯一一条关键路径,并不等于不存在多条关键路径。
如果是多条关键路径,则单是提高一条关键路径上的关键活动速度并不是能导致整个工程缩短工期、
而必须提高同时在几条关键路径上的活动的速度。
代码如下:
1 #include "stdafx.h" 2 #include<iostream> 3 #include<string> 4 using namespace std; 5 #define MAXSIZE 100 6 #define ERROR 0 7 #define OK 1 8 #define INFINITY 65535 9 typedef int Status; 10 11 int *etv, *ltv; //事件最早发生时间和最迟发生时间数组,全局变量 12 int *stack2; //用于存储拓扑序列的栈 13 int top2; //用于stack2的指针 14 15 typedef struct ArcNode //边表结点 16 { 17 int adjvex; //改变所指向的顶点的位置 18 int weight; //用于存储权值 19 struct ArcNode *nextarc; //指向下一条边的指针 20 }ArcNode; 21 typedef struct VNode //顶点表结点 22 { 23 int in; 24 char data; //顶点域,存储顶点信息 25 ArcNode *firstarc; //指向第一条依附该顶点的边的指针 26 }VNode, AdjList[MAXSIZE]; //AdList表示邻接表类型 27 typedef struct //邻接表 28 { 29 AdjList vertices; 30 int vexnum, arcnum; //图的当前顶点数和边数 31 }ALGraph; 32 33 typedef struct 34 { 35 char vexs[MAXSIZE]; //顶点表 36 int arcs[MAXSIZE][MAXSIZE]; //邻接矩阵 37 int vexnum, arcnum; //图的当前点数和边数 38 }AMGraph; 39 40 void CreateUDN(AMGraph &G) //采用邻接矩阵表示法,创建无向网&G 41 { 42 int i, j, w; 43 std::cout << "请输入总顶点数、总边数(空格隔开):" << endl; 44 cin >> G.vexnum >> G.arcnum; //输入总顶点数、总边数 45 std::cout << "请输入顶点信息(空格隔开):" << endl; 46 for (i = 0; i < G.vexnum; i++) //依次输入点的信息 47 { 48 cin >> G.vexs[i]; 49 } 50 for (i = 0; i < G.vexnum; i++) //初始化邻接矩阵,编的权值均为极大值MaxInt 51 for (j = 0; j < G.vexnum; j++) 52 { 53 if (i == j) 54 G.arcs[i][j] = 0; 55 else 56 G.arcs[i][j] = INFINITY; 57 } 58 std::cout << "请输入边的信息(输入顺序:连接点1编号、连接点2编号以及权值):" << endl; 59 for (int k = 0; k < G.arcnum; k++) //构造邻接矩阵 60 { 61 cin >> i >> j >> w; //输入一条边依附的顶点 62 G.arcs[i - 1][j - 1] = w; 63 } 64 65 } 66 67 void CreateALGraph(AMGraph G, ALGraph &GL) 68 { 69 int i, j; 70 ArcNode *e; 71 GL.vexnum = G.vexnum; 72 GL.arcnum = G.arcnum; 73 for (i = 0; i <G.vexnum; i++) //读入顶点信息,建立顶点表 74 { 75 GL.vertices[i].in = 0; 76 GL.vertices[i].data = G.vexs[i]; 77 GL.vertices[i].firstarc = NULL;//将边表置为空表 78 } 79 80 for (i = 0; i<G.vexnum; i++) //建立边表 81 { 82 for (j = 0; j<G.vexnum; j++) 83 { 84 if (G.arcs[i][j] != 0 && G.arcs[i][j]<INFINITY) 85 { 86 e = new ArcNode; 87 e->adjvex = j; //邻接序号为j 88 e->weight = G.arcs[i][j]; 89 e->nextarc = GL.vertices[i].firstarc; //将当前顶点上的指向的结点指针赋值给e 90 GL.vertices[i].firstarc = e; //将当前顶点的指针指向e 91 GL.vertices[j].in++; 92 } 93 } 94 } 95 } 96 97 //拓扑排序 98 Status TopologicalSort(ALGraph GL) 99 { //若GL无回路,则输出拓扑排序序列并返回1,若有回路返回0 100 ArcNode *e; 101 int i, k, gettop; 102 int top = 0; //用于栈指针下标 103 int count = 0; //用于统计输出顶点的个数 104 int *stack; /* 建栈将入度为0的顶点入栈 */ 105 stack = new int[GL.vexnum]; 106 for (i = 0; i<GL.vexnum; i++) 107 if (0 == GL.vertices[i].in) //将入度为0的顶点入栈 108 stack[++top] = i; 109 110 top2 = 0; 111 etv = new int[GL.vexnum]; //事件最早发生时间数组 112 for (i = 0; i<GL.vexnum; i++) 113 etv[i] = 0; //初始化 114 stack2 = new int[GL.vexnum]; //初始化拓扑序列栈 115 116 std::cout << "TopologicalSort: "; 117 while (top != 0) 118 { 119 gettop = stack[top--]; 120 std::cout << GL.vertices[gettop].data << " -> "; 121 count++; //输出i号顶点,并计数 122 123 stack2[++top2] = gettop; //将弹出的顶点序号压入拓扑序列的栈 */ 124 125 for (e = GL.vertices[gettop].firstarc; e; e = e->nextarc) 126 { 127 k = e->adjvex; 128 if (!(--GL.vertices[k].in))//将i号顶点的邻接点的入度减1,如果减1后为0,则入栈 129 stack[++top] = k; 130 131 if ((etv[gettop] + e->weight)>etv[k]) //求各顶点事件的最早发生时间etv值 132 etv[k] = etv[gettop] + e->weight; 133 } 134 } 135 std::cout << endl; 136 if (count < GL.vexnum) 137 return ERROR; 138 else 139 return OK; 140 } 141 142 //求关键路径,GL为有向网,输出G的各项关键活动 143 void CriticalPath(ALGraph GL) 144 { 145 ArcNode *e; 146 int i, gettop, k, j; 147 int ete, lte; //声明活动最早发生时间和最迟发生时间变量 148 TopologicalSort(GL); //求拓扑序列,计算数组etv和stack2的值 149 ltv = new int[GL.vexnum]; //事件最早发生时间数组 150 for (i = 0; i<GL.vexnum; i++) 151 ltv[i] = etv[GL.vexnum - 1]; //初始化 152 153 std::cout << "etv: "; 154 for (i = 0; i < GL.vexnum; i++) 155 std::cout << etv[i] << "->"; 156 std::cout << endl; 157 158 while (top2 != 0) //出栈是求ltv 159 { 160 gettop = stack2[top2--]; 161 for (e = GL.vertices[gettop].firstarc; e; e = e->nextarc)//求各顶点事件的最迟发生时间ltv值 162 { 163 k = e->adjvex; 164 if (ltv[k] - e->weight < ltv[gettop]) 165 ltv[gettop] = ltv[k] - e->weight; 166 } 167 } 168 169 std::cout<<"ltv: "; 170 for (i = 0; i<GL.vexnum; i++) 171 std::cout << ltv[i] << "->"; 172 std::cout << endl; 173 174 for (j = 0; j<GL.vexnum; j++) //求ete,lte和关键活动 175 { 176 for (e = GL.vertices[j].firstarc; e; e = e->nextarc) 177 { 178 k = e->adjvex; 179 ete = etv[j]; //活动最早发生时间 180 lte = ltv[k] - e->weight; //活动最迟发生时间 181 if (ete == lte) //两者相等即在关键路径上 182 std::cout << "<" << GL.vertices[j].data << " - " << GL.vertices[k].data << ">," << "Length:" << e->weight << endl; 183 } 184 } 185 } 186 int main() 187 { 188 AMGraph G; 189 ALGraph GL; 190 CreateUDN(G); 191 CreateALGraph(G,GL); 192 CriticalPath(GL); 193 return 0; 194 }
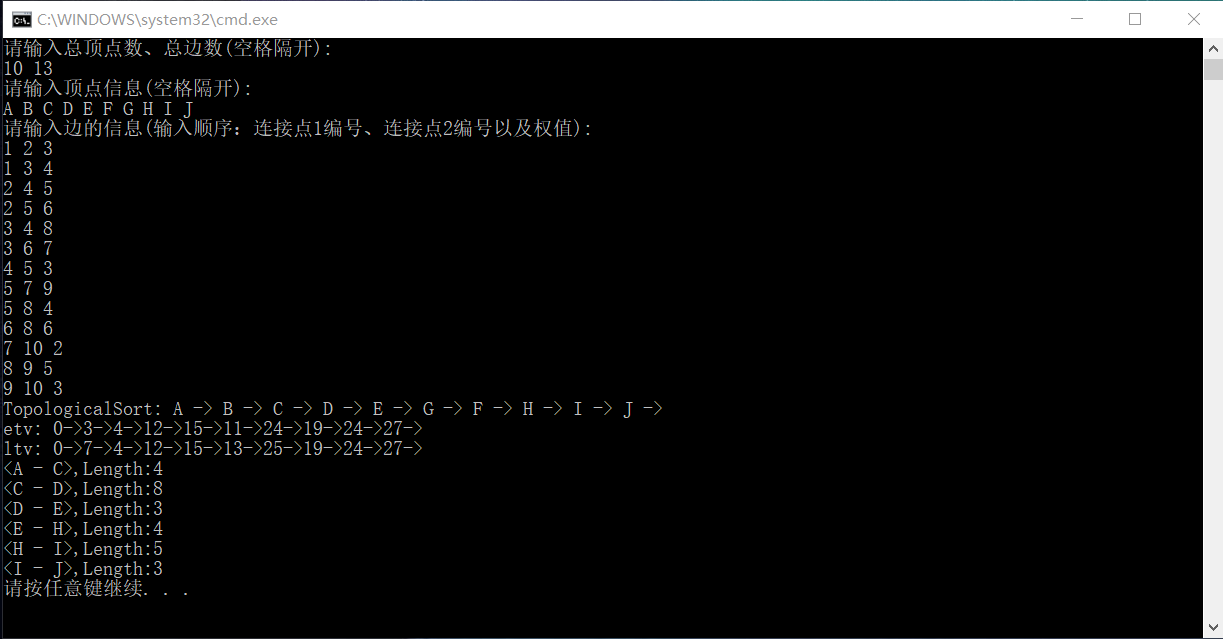
测试结果: