数据结构之拓扑排序
算法解析(图片内容来自《大话数据结构》这本书不错哦):
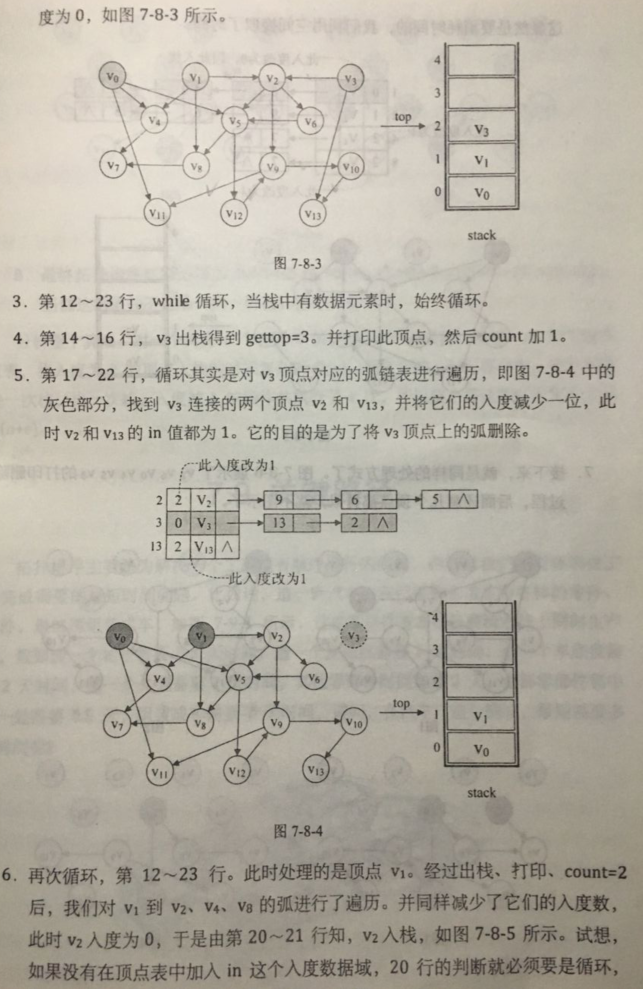
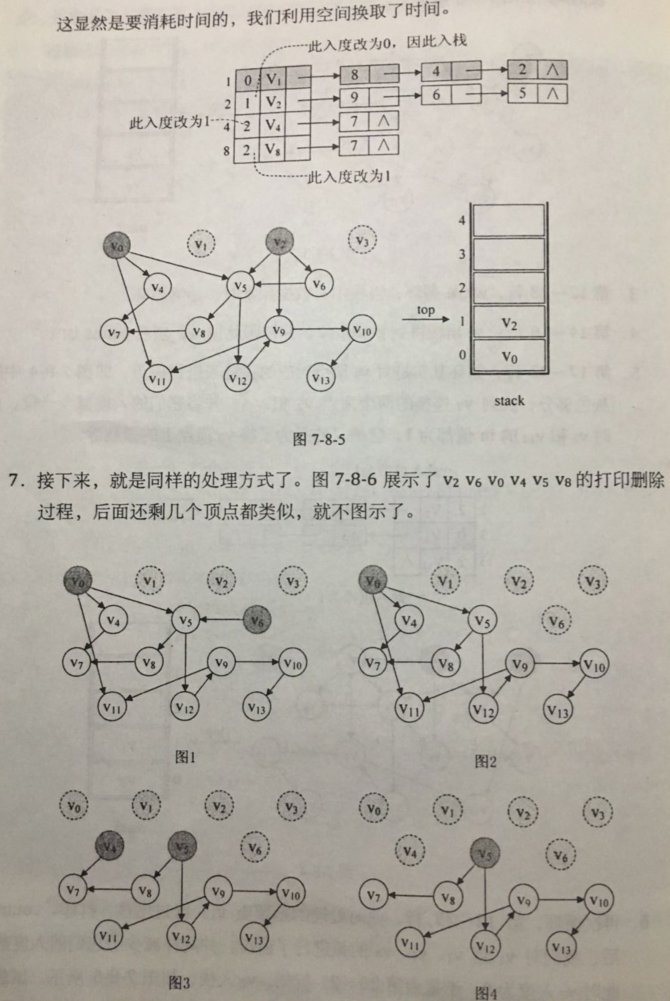
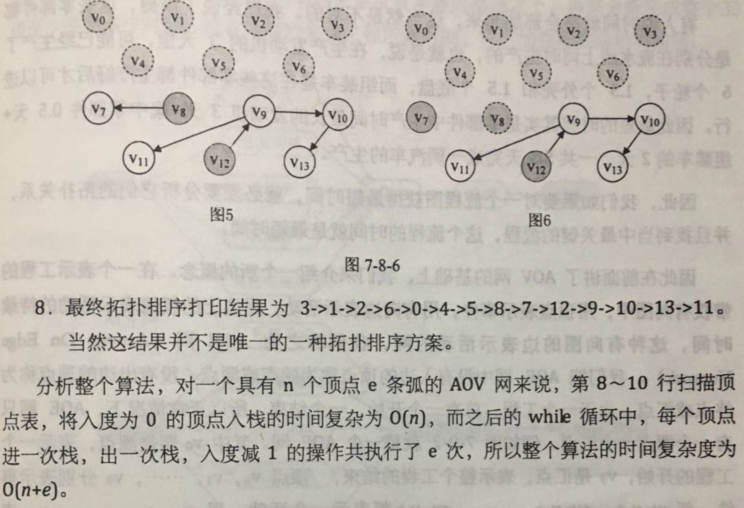
代码如下:
1 #include "stdafx.h" 2 #include<iostream> 3 #include<string> 4 using namespace std; 5 #define MAXSIZE 100 6 #define ERROR 0 7 #define OK 1 8 #define INFINITY 65535 9 typedef int Status; 10 typedef struct ArcNode //边表结点 11 { 12 int adjvex; //改变所指向的顶点的位置 13 struct ArcNode *nextarc; //指向下一条边的指针 14 }ArcNode; 15 typedef struct VNode //顶点表结点 16 { 17 int in; 18 char data; //顶点域，存储顶点信息 19 ArcNode *firstarc; //指向第一条依附该顶点的边的指针 20 }VNode, AdjList[MAXSIZE]; //AdList表示邻接表类型 21 typedef struct //邻接表 22 { 23 AdjList vertices; 24 int vexnum, arcnum; //图的当前顶点数和边数 25 }ALGraph; 26 27 typedef struct 28 { 29 char vexs[MAXSIZE]; //顶点表 30 int arcs[MAXSIZE][MAXSIZE]; //邻接矩阵 31 int vexnum, arcnum; //图的当前点数和边数 32 }AMGraph; 33 34 void CreateUDN(AMGraph &G) //采用邻接矩阵表示法，创建无向网&G 35 { 36 int i, j, w; 37 cout << "请输入总顶点数、总边数(空格隔开):" << endl; 38 cin >> G.vexnum >> G.arcnum; //输入总顶点数、总边数 39 cout << "请输入顶点信息(空格隔开):" << endl; 40 for (i = 0; i < G.vexnum; i++) //依次输入点的信息 41 { 42 cin >> G.vexs[i]; 43 } 44 for (i = 0; i < G.vexnum; i++) //初始化邻接矩阵，编的权值均为极大值MaxInt 45 for (j = 0; j < G.vexnum; j++) 46 G.arcs[i][j] = 0; 47 cout << "请输入边的信息(输入顺序：连接点1编号，连接点2编号):" << endl; 48 for (int k = 0; k < G.arcnum; k++) //构造邻接矩阵 49 { 50 cin >> i >> j; //输入一条边依附的顶点 51 G.arcs[i-1][j-1] = 1; 52 } 53 } 54 55 void CreateALGraph(AMGraph G, ALGraph &GL) 56 { 57 int i, j; 58 ArcNode *e; 59 GL.vexnum = G.vexnum; 60 GL.arcnum = G.arcnum; 61 for (i = 0; i <G.vexnum; i++) //读入顶点信息，建立顶点表 62 { 63 GL.vertices[i].in = 0; 64 GL.vertices[i].data = G.vexs[i]; 65 GL.vertices[i].firstarc = NULL;//将边表置为空表 66 } 67 68 for (i = 0; i<G.vexnum; i++) //建立边表 69 { 70 for (j = 0; j<G.vexnum; j++) 71 { 72 if (G.arcs[i][j] == 1) 73 { 74 e = new ArcNode; 75 e->adjvex = j; //邻接序号为j 76 e->nextarc = GL.vertices[i].firstarc;//将当前顶点上的指向的结点指针赋值给e 77 GL.vertices[i].firstarc = e;//将当前顶点的指针指向e 78 GL.vertices[j].in++; 79 } 80 } 81 } 82 } 83 84 Status TopologicalSort(ALGraph GL) 85 { 86 ArcNode *e; 87 int i, k, gettop; 88 int top = 0; //用于栈指针下标 89 int count = 0; // 用于统计输出顶点的个数 90 int *stack; //建栈将入度为0的顶点入栈 91 stack = new int[GL.vexnum]; 92 for (i = 0; i<GL.vexnum; i++) 93 if (0 == GL.vertices[i].in) //将入度为0的顶点入栈 94 stack[++top] = i; 95 while (top != 0) 96 { 97 gettop = stack[top--]; 98 cout << GL.vertices[gettop].data<<"->"; 99 count++; //输出i号顶点，并计数 100 for (e = GL.vertices[gettop].firstarc; e; e = e->nextarc) 101 { 102 k = e->adjvex; 103 if (!(--GL.vertices[k].in)) //将i号顶点的邻接点的入度减1，如果减1后为0，则入栈 104 stack[++top] = k; 105 } 106 } 107 cout << endl; 108 if (count <GL.vexnum) 109 return ERROR; 110 else 111 return OK; 112 } 113 114 int main() 115 { 116 AMGraph G; 117 ALGraph GL; 118 int result; 119 CreateUDN(G); 120 CreateALGraph(G,GL); 121 result = TopologicalSort(GL); 122 cout << "result:" << result << endl; 123 return 0; 124 }
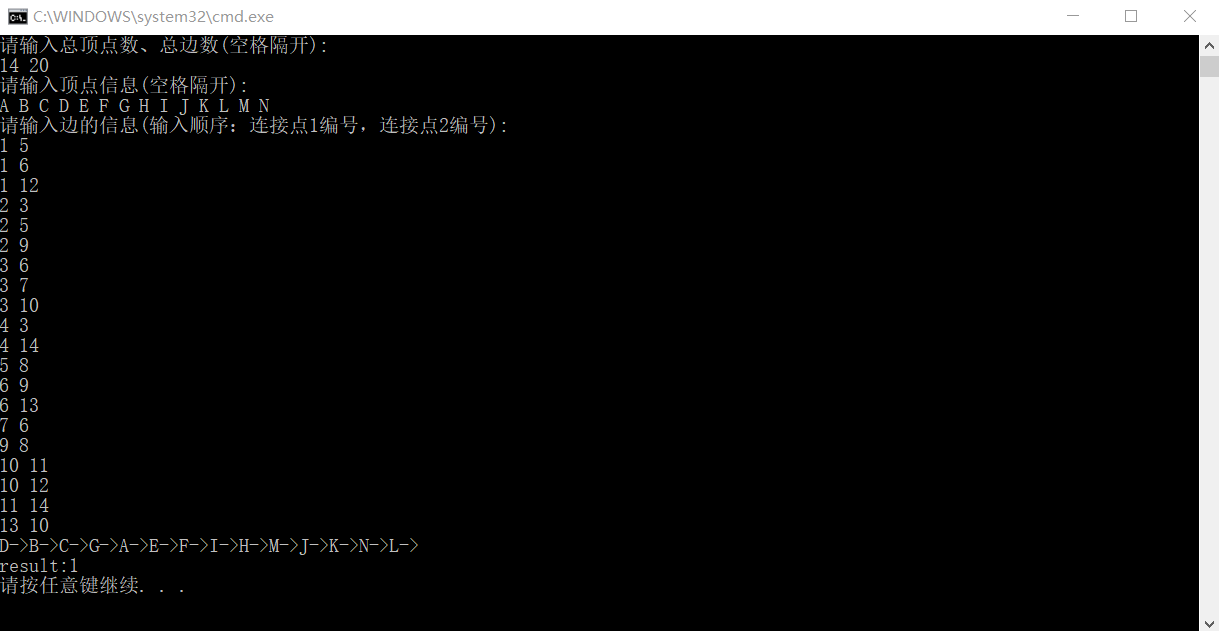
示例结果(就是上面那几张图片的示例):
