数据结构之最短路径(1) [迪杰斯特拉算法]

迪杰斯特拉算法介绍：

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

基本思想：

通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是"起点s到该顶点的路径"。然后，从U中找出路径最短的顶点，并将其加入到S中；

接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 ... 重复该操作，

直到遍历完所有顶点。

操作步骤：

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

(2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

迪杰斯特拉算法图解

 

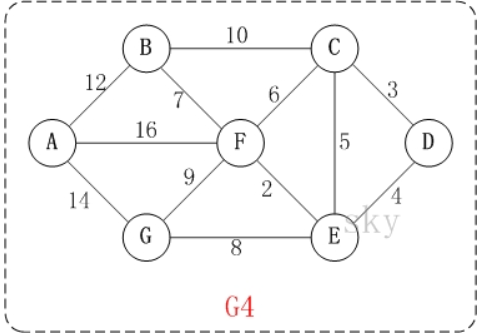
以上图G4为例，来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。

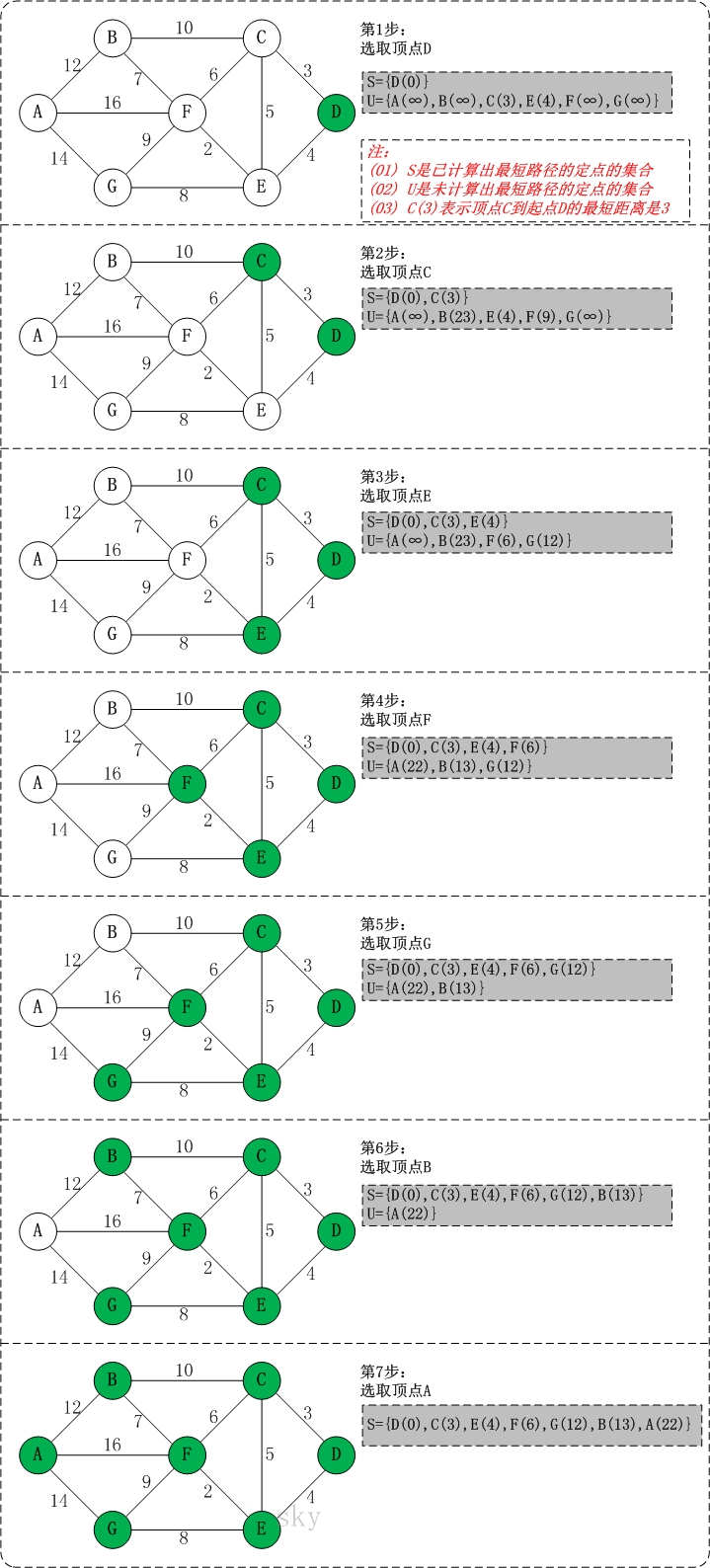
初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！

第1步：将顶点D加入到S中。 
此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。 
上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。 
此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。 
上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。 
此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。 
此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。 
此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。 
此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。 
此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

代码如下:

 

#include "stdafx.h"
#include<iostream>
#include<string>
#define MAX_VERTEX_NUM 100
#define INFINITY 65535
typedef int Pathmatirx[MAX_VERTEX_NUM];//存放最短路径下标的数组
typedef int ShortPathTable[MAX_VERTEX_NUM];//存放到各顶点最短路径的权值之和
using namespace std;
typedef struct Graph            //有向图的邻接矩阵
{
    char vexs[MAX_VERTEX_NUM];  //存放顶点的数组
    int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];//定义一个临界矩阵
    int vexnum, arcnum;         //总顶点数、总边数
}Graph;

int LocateVex(Graph G, char ch) //搜索
{
    for (int i = 0; i < G.vexnum; i++)
        if (G.vexs[i] == ch)
            return i;
    return -1;
}

void CreateGraph(Graph &G)      //创建无向图
{
    char c1, c2;                //弧尾、弧头
    int i, j, weight;           //weight为权重
    cout << "请输入总顶点数、总边数(空格隔开):";
    cin >> G.vexnum >> G.arcnum;
    cout << "请输入顶点信息(空格隔开):" << endl;
    for (i = 0; i < G.vexnum; i++)  
    {
        cin >> G.vexs[i];
    }
    for (i = 0; i < G.vexnum; i++) 
        for (j = 0; j < G.vexnum; j++)
            G.arcs[i][j] = INFINITY;
    cout << "请输入弧尾、弧头以及权值:" << endl;
    for (int k = 0; k < G.arcnum; k++)
    {
                 cin >> c1 >> c2 >> weight;
                 i = LocateVex(G, c1);
                 j = LocateVex(G, c2);
                 G.arcs[i][j] = weight;
     }
}

void ShortestPath_Dijkstra(Graph G, int v0, int prev[], int dist[])//迪杰斯特拉算法
{    //求有向图G的v0顶点到其余顶点v最短路径prev[v]及带权长度dist[v]，prev[v]的值为前驱顶点下标，dist[v]表示v0到v的最短路径长度之和。
    int v , w, k, min;
    int final[MAX_VERTEX_NUM];  //final[w]=1表示求得顶点v0至v(w)的最短路径
    for (v = 0; v < G.vexnum; v++)//初始化数据
    {
        final[v] = 0;           //全部顶点初始化为未知最短路径状态
        dist[v] = G.arcs[v0][v];//将与v0点有连线的顶点加上权值
        prev[v] = 0;            //初始化路径数组prev为0
    }
    dist[v0] = 0;               //v0至v0的路径为0
    final[v0] = 1;              //v0至v0不需要求路径
    for (v = 1; v < G.vexnum; v++)//开始主循环，每次求得v0到某个v顶点的最短路径
    {
        min = INFINITY;        //当前所知离v0顶点最近的距离
        for (w = 0; w < G.vexnum; w++)//寻找v0最近的顶点
        {
            if (!final[w] && dist[w] < min)
            {
                k = w;
                min = dist[w];  //w顶点离v0顶点最近
            }
        }
        final[k] = 1;           //将目前找到的最近的顶点值为1
        for (w = 0; w < G.vexnum; w++)//修正当前最短路径及距离
        {      //如果经过v顶点的路径比现在这条路径的长度短的话
            if (!final[w] && (min + G.arcs[k][w] < dist[w]))
            {   //说明找到了了更短的路径，修改dist[w]和prev[w]
                dist[w] = min + G.arcs[k][w];//修改路径长度
                prev[w] = k;
            }
        }
    }
    cout << "起始点:";          //一下就是输出函数
    cout << G.vexs[v0]<<endl;
    cout << "从开始点" << G.vexs[v0] << "到各点的最短距离为：" << endl;
    for (int i = 0; i < G.vexnum; i++)
        cout << "到" << G.vexs[i] << "的距离为：" << dist[i] << endl;
}

int main()
{
    Graph G;
    int prev[MAX_VERTEX_NUM];
    int dist[MAX_VERTEX_NUM];
    int v0;
    CreateGraph(G);
    cout << "Please input v0:";
    cin >> v0;
    ShortestPath_Dijkstra(G, v0, prev, dist);
}

 

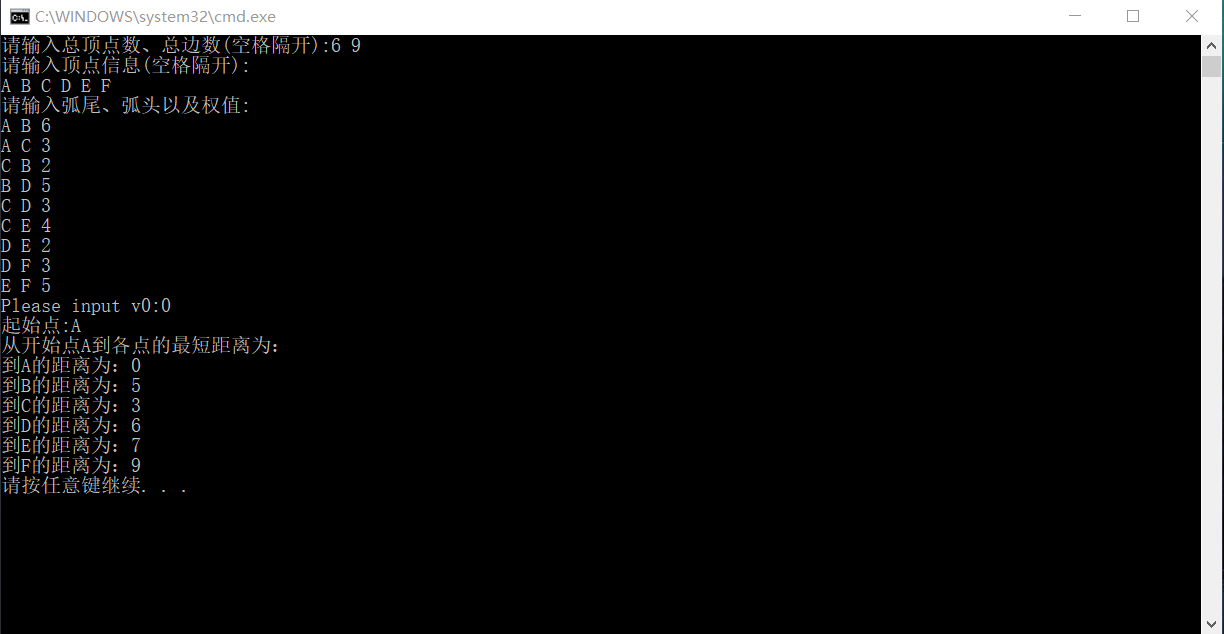
示例展示:

 

参考资料：http://www.cnblogs.com/skywang12345/p/3711512.html